希尔密码（加密、解密、破解）

简介

希尔密码是运用基本矩阵论原理的替换密码，由Lester S. Hill在1929年发明。

每个字母当作26进制数字：A=0, B=1, C=2… 一串字母当成n维向量，跟一个n×n的矩阵相乘，再将得出的结果模26。（注意用作加密的矩阵（即密匙）在 必须是可逆的，否则就不可能解码。只有矩阵的行列式和26互质，才是可逆的。）

例子

用希尔密码对明文串 x = ecnu 进行加密，

密钥矩阵: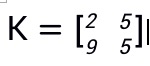

加密

密文向量 = 明文向量 * 密钥矩阵 (mod 26)
1.先将明文串对应英文字母编码表进行数字转化 4 2 13 20
然后两两一组写成矩阵形式：

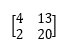
2.接下来开始加密

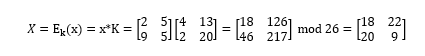
得到密文矩阵后，按照分组对应的向量转成字母:
SUWJ

解密

解密和加密类似，先通过刚刚的方法计算出 模 m 的逆矩阵，然后用 A−1 再进行解密:

求逆矩阵的方法：

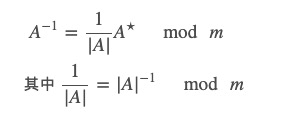
实际二阶矩阵的逆矩阵就是：

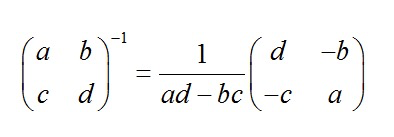
mod 26后 ，然后用上述相同的方法转换成明文串即可。

三阶同理：

分析与破解

例子：
假设已知明文friday利用n=2的希尔密码加密，得到密文VYUZSM，求秘钥K

n等于2，说明把friday分成3段，矩阵是2*2的

根据字母与整数的对应关系：
(5,17)—->(21,24),
(8,3)—->(20,25),
(0,24)—>(18,12),得到

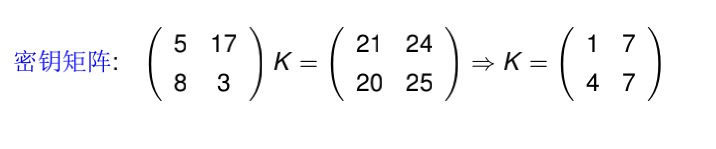
用(0,24)—>(18,12)验证K:

正确！得到密钥K就随便破解密文了