博客

前序遍历非递归

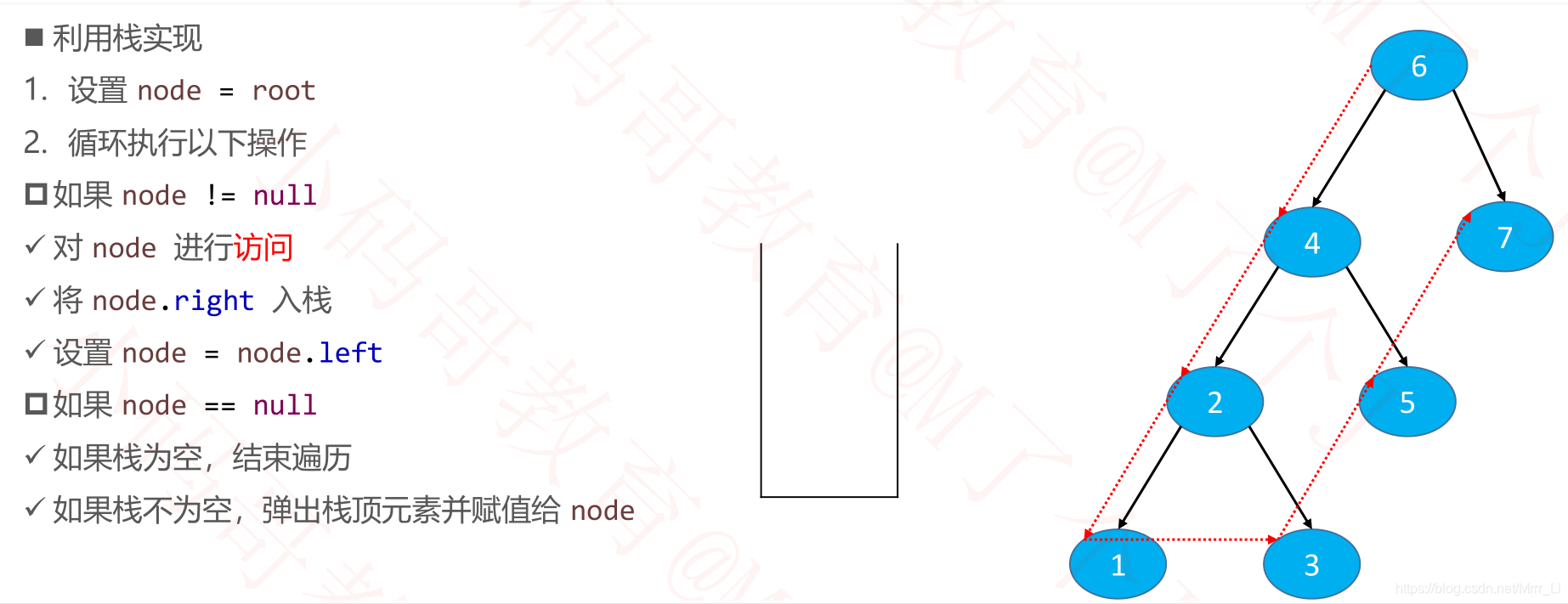
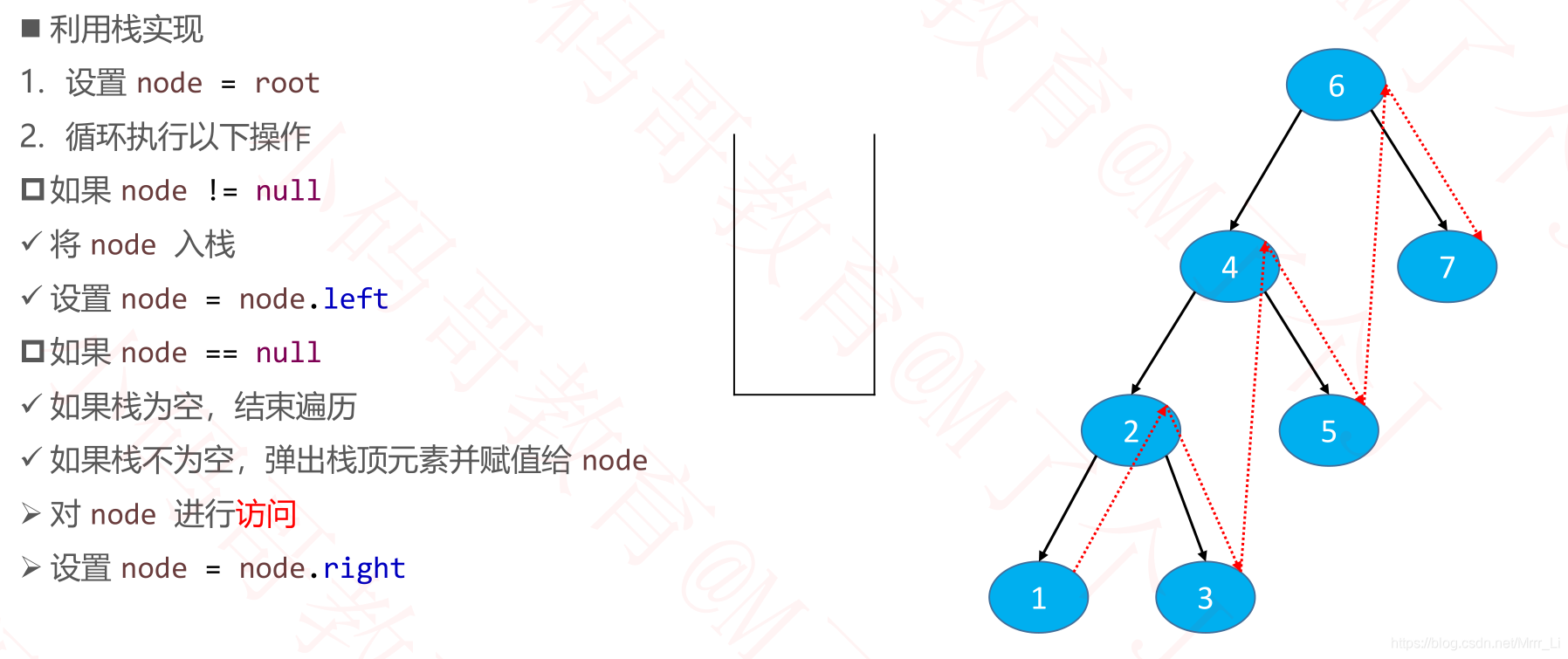
然后node再进行前序遍历

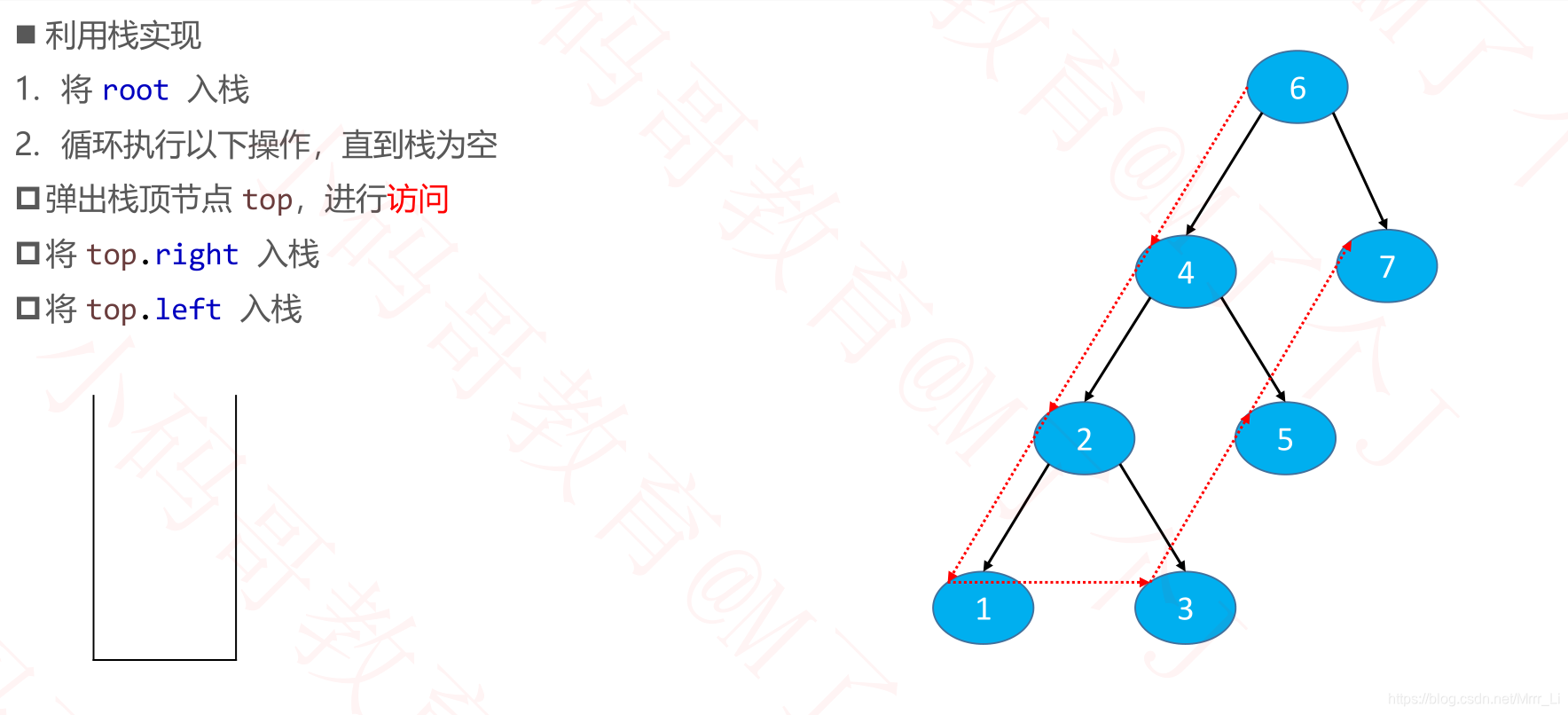
中序遍历非递归

让node.right进行中序遍历


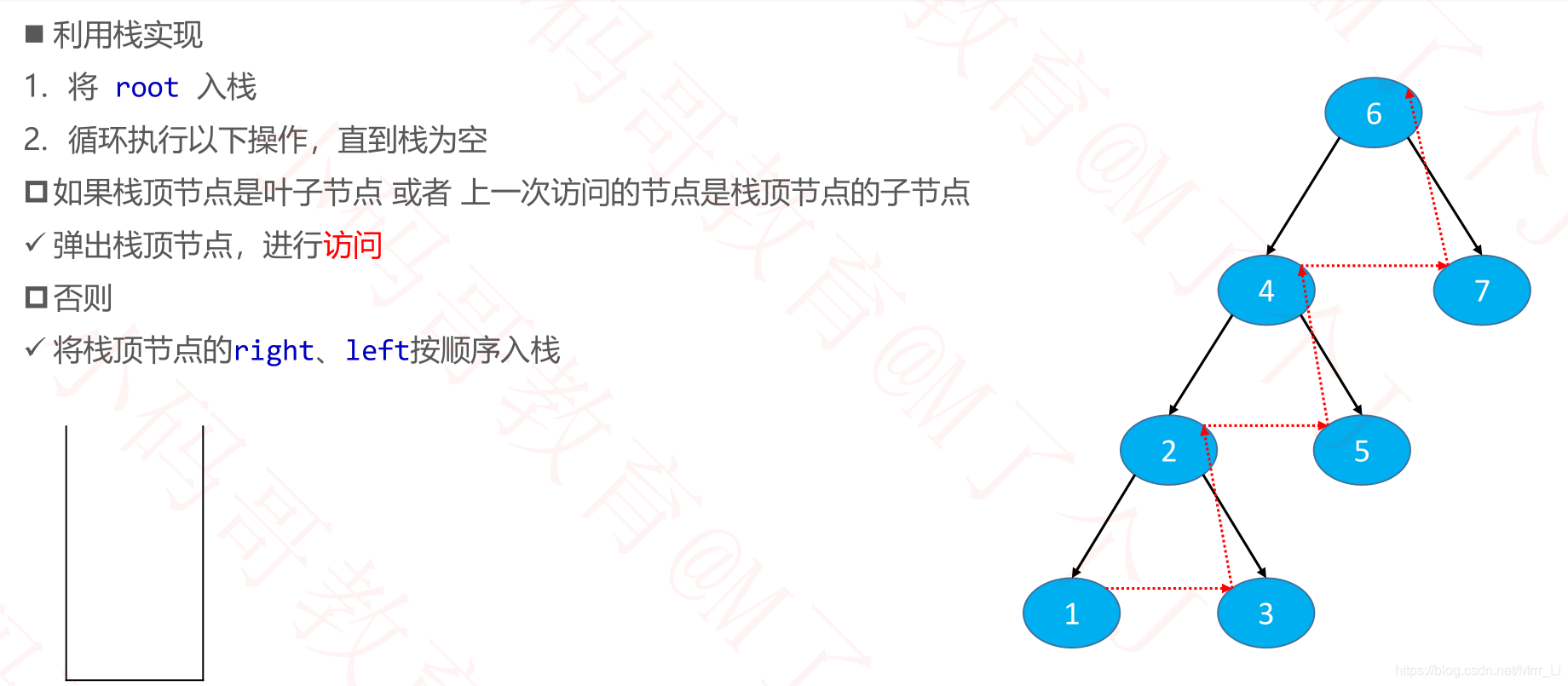
后续遍历非递归

public void preorder(Visitor<E> visitor) {
		if (visitor == null || root == null) return;
		Stack<Node<E>> stack = new Stack<>();
		stack.push(root);
		while (!stack.isEmpty()) {
			Node<E> node = stack.pop();
			// 访问node节点
			if (visitor.visit(node.element)) return;
			if (node.right != null) {
				stack.push(node.right);
			}
			if (node.left != null) {
				stack.push(node.left);
			}
		}
	}
	
	public void preorder2(Visitor<E> visitor) {
		if (visitor == null || root == null) return;
		Node<E> node = root;
		Stack<Node<E>> stack = new Stack<>();
		while (true) {
			if (node != null) {
				// 访问node节点
				if (visitor.visit(node.element)) return;
				// 将右子节点入栈
				if (node.right != null) {
					stack.push(node.right);
				}
				// 向左走
				node = node.left;
			} else if (stack.isEmpty()) {
				return;
			} else { 
				// 处理右边
				node = stack.pop();
			}
		}
	}
	
	public void inorder(Visitor<E> visitor) {
		if (visitor == null || root == null) return;
		Node<E> node = root;
		Stack<Node<E>> stack = new Stack<>();
		while (true) {
			if (node != null) {
				stack.push(node);
				// 向左走
				node = node.left;
			} else if (stack.isEmpty()) {
				return;
			} else {
				node = stack.pop();
				// 访问node节点
				if (visitor.visit(node.element)) return;
				// 让右节点进行中序遍历
				node = node.right;
			}
		}
	}
	
	public void postorder(Visitor<E> visitor) {
		if (visitor == null || root == null) return;
		// 记录上一次弹出访问的节点
		Node<E> prev = null;
		Stack<Node<E>> stack = new Stack<>();
		stack.push(root);
		while (!stack.isEmpty()) {
			Node<E> top = stack.peek();
			if (top.isLeaf() || (prev != null && prev.parent == top)) {
				prev = stack.pop();
				// 访问节点
				if (visitor.visit(prev.element)) return;
			} else {
				if (top.right != null) {
					stack.push(top.right);
				}
				if (top.left != null) {
					stack.push(top.left);
				}
			}
		}
	}