博客

火车进出栈问题

一列火车n节车厢，依次编号为1,2,3,…,n。

每节车厢有两种运动方式，进栈与出栈，问n节车厢出栈的可能排列方式有多少种。

输入格式

输入一个整数n，代表火车的车厢数。

输出格式

输出一个整数s表示n节车厢出栈的可能排列方式数量。

数据范围

1≤n≤60000

输入样例：

3

输出样例：

5

分析：

看到这种问题我们首先想到的方法就是模拟出栈进栈的操作在记录符合的次数，而我们模拟的话实际运用的就是dfs搜索，每一层dfs搜索都有两个方向（开头和结尾不算的话），即搜索的深度为最大60000，调用搜索函数最多2^(60000*2)；这明显是不可行的。因此我们可以将进出栈操作数字化：

（1）如果我们把dfs搜索的结果数字化为2*60000=120000位2进制的话，那么每一位就表示的是在当前的操作方向（假设1为进栈，0为出栈）,这里我们根据样例来说：

当n=3时，我们有五种操作：

111000（进进进出出出）

110010（进进出出进出）

110100（进进出进出出）

101100（进出进进出出）

101010（进出进出进出）

就本身的进出栈操作我们知道不论在那一步操作进栈的个数一定是大于等于出栈的操作；那么反映到二进制上来说就是，对于每一位从第0位到当前位的1的个数一定大于等于0的个数，但如果我们根据这个性质列举每一个这样的超长二进制数然后在判断的话时间复杂度也是非常大的，因此这里我们可以把二进制数图形化：

（2）我们建立一个坐标系，然后把二进制中的1表示向右移动一位，0表示向上移动一位（必须这样表示），我们把样例的二进制表示一下：

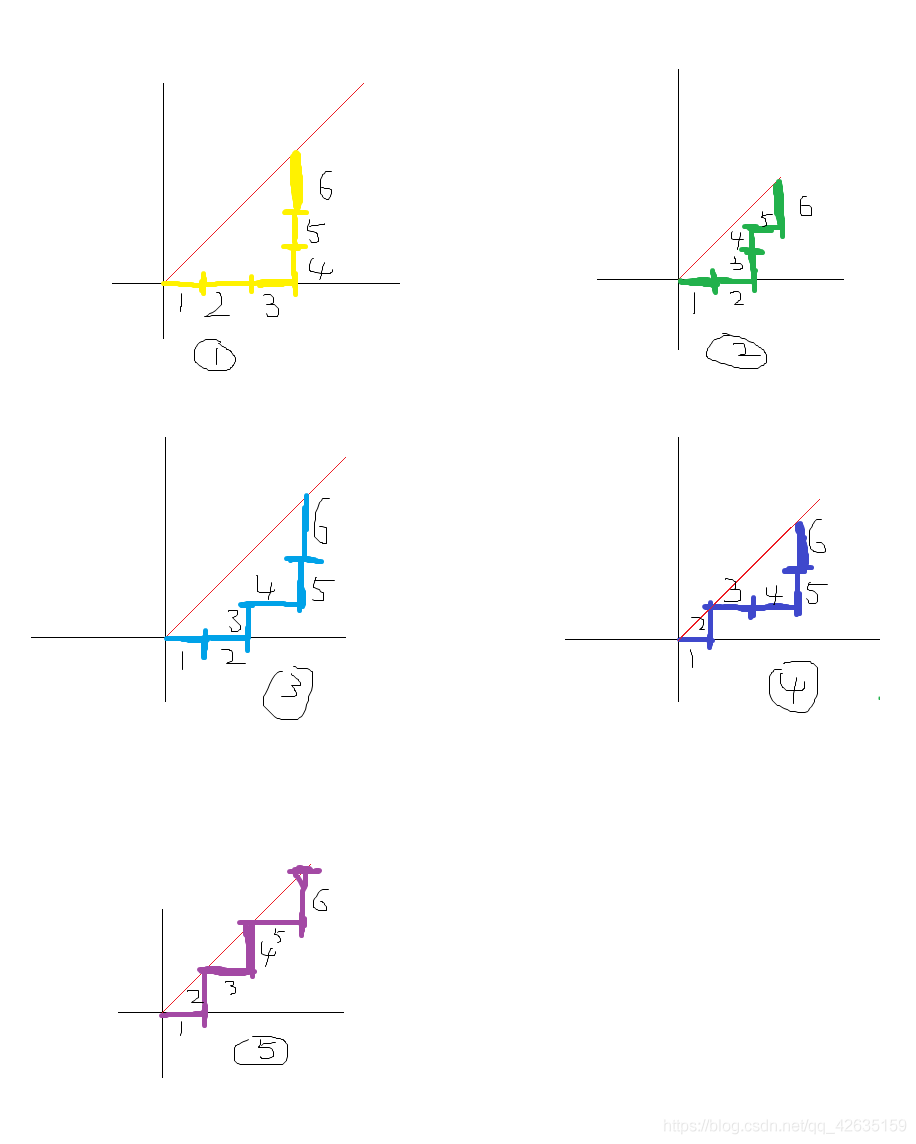
这样我们就把所有的合法的进出栈操作图形化为折线图了，我们由此可以形象的看到可以的进出栈操作在图形化下都是在y=x，以下的；到这里我们还是不能直接计算因为如果按照图形直接计算的话相当于还是dfs搜索；

这里其实是典型的卡特兰数：

因为不能直接计算结果的话，我们换一种思路就是用总的个数减去不合法的个数：

总的个数就是我的进出栈可以任意操作，也就是2*n的二进制中的n个1和n个0可以任意填，那么总的个数就是

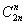
下面我们看几个错误的入栈出栈的操作：

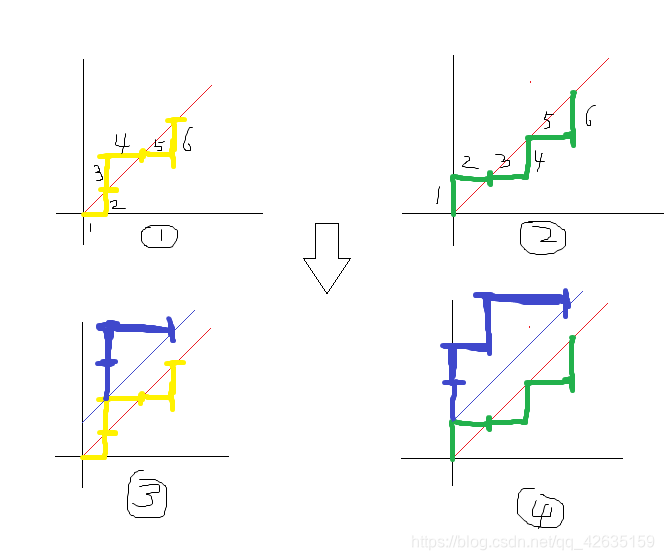
其中前两个图是错误的出入栈操作，因为出现错误那么折线图一定会穿过y=x直线，因此我们做y=x+1直线，以第一次穿过y=x点之后的折线按照y=x+1对称的话所有错误的折线最终都会到达（n-1,n+1）的点，即所有的能到达(n-1,n+1)的折线都表示一个错误的出入栈操作，这种情况有:

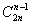
因此我们现在的任务就是计算：

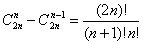
由于这里的n=60000，计算出来的组合数肯定会特别大，因此这里用到高精度的算法。这里我们如果按照普通的计算方法先算分子在算分母，在相处的话数据范围肯定会超过最终结果，因为（2n）！的数值肯定会超过最终的结果，我们这里做的操作是：将阶乘的形式化为素数的幂指数之积的形式，因此我们只需要先把分子分母的幂指数相减在展开这样计算的过程就是稳定的增加到最终结果的过程。

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=60010,M=120010;//基础数据范围为60000，出入栈选择范围为120010。
ll res[N],tt;//res数组为高精度数组，每一位高精度数组压位10^9，以最大数据(2n)!=(120000)!来说是足够用的
//tt为高精度数组的位数 
int st[M];//st用于存储幂指数表示方法的幂数次数，用于下一步的转化成高精度数组 
bool q[M];//利用筛素数的方法q数组内筛出2n范围内的素数
int get(int n,int p)
{  //该函数用于计算n!中p存在的幂指数次数的总次数
//即get(3,3)=1,get(4,3)=1,get(6,3)=2,get(9,3)=4;
//求n!中p的幂次数即=n/p+n/(p^2)+n/(p^3)……直到n/(p^k)=0时，k为n中包含的p的幂次数，这里不加证明
	int s=0;
	while(n)s+=n/p,n/=p;
	return s; 
}
void multi(ll b)
{
	ll t=0;//t为低位的进位
	for(int i=0;i<=tt;i++)
	{
		res[i]=res[i]*b+t;//每一位高精度数组压9位 
		t=res[i]/1000000000;
		res[i]%=1000000000;
	 } 
	 if(t)//当最后又进位时高精度数组长度加一，这里长度最多加一。 
	 	res[++tt]=t;
	 
}
void out(){
	printf("%lld",res[tt]);
	for(int i=tt-1;i>=0;i--)
	printf("%09lld",res[i]);
	cout<<endl;
}
int main(){
	int n;
	cin>>n;
	for(int i=2;i<=2*n;i++)
	  if(!q[i])//如果当前的数为素数的话那么他的倍数都不是素数，都筛去
	  for(int j=i+i;j<=2*n;j+=i)
	  q[j]=true;
	  
	  //将整体的公式用幂指数的形式表示，这样分子分母相除的形式就表示为幂指数相减的形式 
	  //分解幂指数形式时，要表示为素数的幂指数形式 
	  for(int i=2;i<=2*n;i++)
	  if(!q[i])
	  {//get(n,i)表示的是n!中素数i存在的总次数 
	  	st[i]=get(2*n,i)-get(n,i)-get(n+1,i);
	  }
	  
	  res[0]=1;
	  for(int i=2;i<=2*n;i++)
	 if(!q[i])
	 {  //将得到的幂指数次数存储的数组展开成高精度 
	 	while(st[i]--)multi(i);
	 }
	  out();
	  return 0; 
	    
}