计算STEC程序中遇到的一些问题小结
文章目录
1. 相关知识背景
1.1 穿刺点及电离层投影函数原理
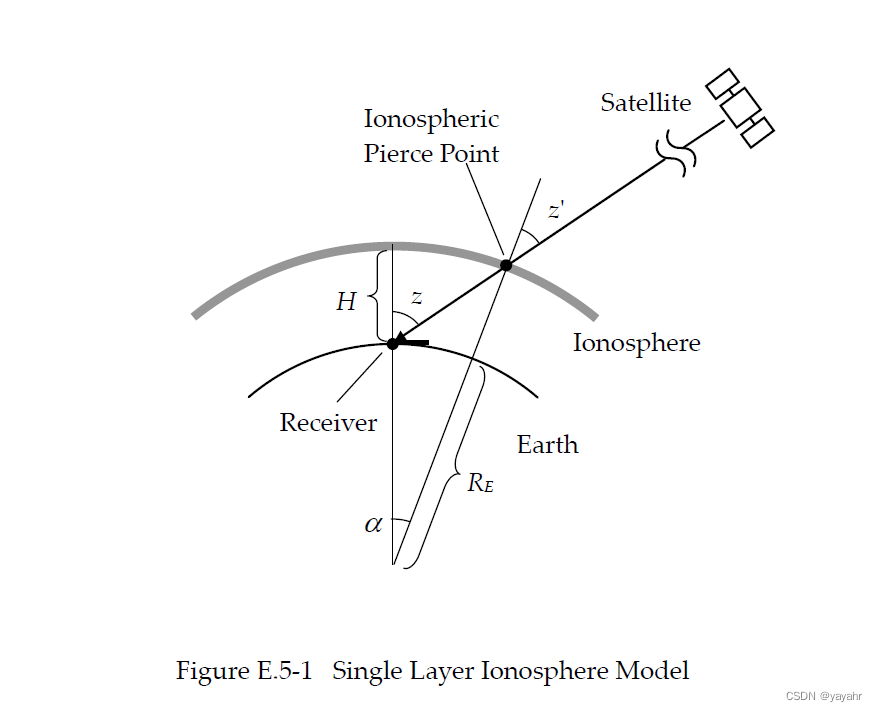
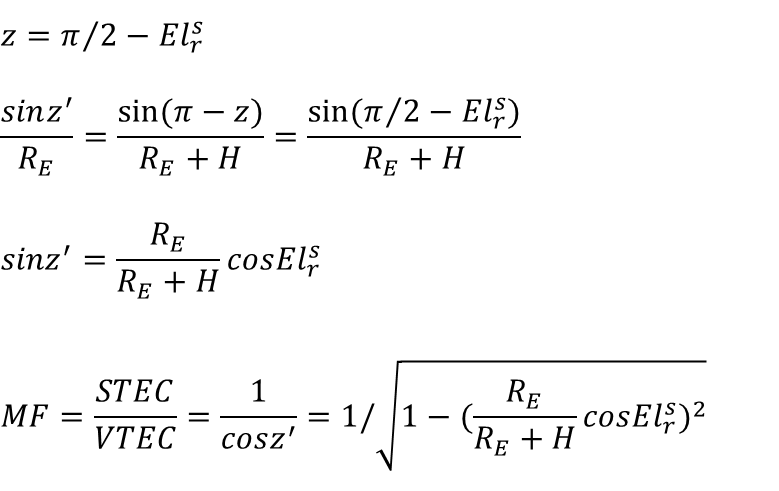
1.2 根据接收机和卫星xyz坐标(方法一)计算穿刺点:
首先将接收机和卫星xyz坐标转化成经纬度,再根据以下函数计算卫星高度角,利用GAMP中计算穿刺点,再插值得到VTEC,经过投影函数计算得到STEC。
//readsat_xyzpos、readrec_xyzpos分别为卫星、接收机xyz坐标
ecef2pos(readsat_xyzpos, readsat_llhpos);
ecef2pos(readrec_xyzpos, readrec_llhpos);//xyz转llh
geodist(readsat_xyzpos, readrec_xyzpos, e);//compute geometric distance and receiver-to-satellite unit vector
satazel(readrec_llhpos, e, azel);//satellite azimuth/elevation angle
ele = azel[1] * R2D;//卫星高度角
得到卫星高度角后,再结合接收机位置(llh)、地球半径、电离层单层高度(标准投影函数通常取450km),利用ionppp计算穿刺点位置(llh)
mf = ionppp(pos, azel, nav->tec->rb, hion, posp);//返回值为标准投影函数值
其中,ionppp函数的各项参数说明如下:
/* ionospheric pierce point position -------------------------------------------
* compute ionospheric pierce point (ipp) position and slant factor
* args : double *pos I receiver position {lat,lon,h} (rad,m)
* double *azel I azimuth/elevation angle {az,el} (rad)
* double re I earth radius (km)
* double hion I altitude of ionosphere (km)
* double *posp O pierce point position {lat,lon,h} (rad,m)
* return : slant factor
* notes : see ref [2], only valid on the earth surface
* fixing bug on ref [2] A.4.4.10.1 A-22,23
*-----------------------------------------------------------------------------*/
extern double ionppp(const double *pos, const double *azel, double re,
double hion, double *posp)
根据当前时刻与读取的每幅GIM图时刻进行比对,找出对应时刻的GIM图位置:
for (itt = 0; itt < nav->nt; itt++)
{
if (timediff(nav->tec[itt].time, time) > 0.0) break;
}// itt判断当前用哪张GIM map
if (itt == 0 || itt >= nav->nt)
{
printf("%s: tec grid out of period\n", time_str(time, 0));
return 0;
}
if ((tt = timediff(nav->tec[itt].time, nav->tec[itt - 1].time)) == 0.0)
{
printf("tec grid time interval error\n");
return 0;
}
利用找出的GIM对应的tec、穿刺点位置posp可以计算出vtec,此处分别计算当前GIM图+下一张GIM图,根据时间进行线性插值的方法,得到最终vtec:
stat[0] = interptec(nav->tec + itt - 1, 0, posp21, vtec2, rms2);
stat[1] = interptec(nav->tec + itt, 0, posp22, vtec2 + 1, rms2 + 1);
if (stat[0] && stat[1]) { /* linear interpolation by time */
a = timediff(time, nav->tec[itt - 1].time) / tt;
vtec22 = vtec2[0] * (1.0 - a) + vtec2[1] * a;
}
else if (stat[0]) { /* nearest-neighbour extrapolation by time */
vtec22 = vtec2[0];
}
else {
vtec22 = vtec2[1];
}
ionppp函数中,计算穿刺点的方法在rtklib手册上有详细介绍:
α
=
z
−
z
′
\alpha=z-z^{‘}
α
=
z
−
z
′
ϕ
i
p
p
=
a
r
c
s
i
n
(
c
o
s
α
s
i
n
ϕ
r
+
s
i
n
α
c
o
s
ϕ
r
c
o
s
A
z
r
s
)
\phi_{ipp}=arcsin(cos\alpha sin\phi_r + sin\alpha cos\phi_r cosAz^{s}_{r})
ϕ
i
p
p
=
a
r
c
s
i
n
(
c
o
s
α
s
i
n
ϕ
r
+
s
i
n
α
c
o
s
ϕ
r
c
o
s
A
z
r
s
)
(
ϕ
r
>
7
0
°
a
n
d
t
a
n
α
c
o
s
A
z
r
s
>
t
a
n
(
π
/
2
−
ϕ
r
)
)
o
r
(
ϕ
r
<
−
7
0
°
a
n
d
−
t
a
n
α
c
o
s
A
z
r
s
>
t
a
n
(
π
/
2
+
ϕ
r
)
)
)
(\phi_r>70^{°} \quad and \quad tan\alpha cosAz^{s}_{r} > tan(\pi/2-\phi_r)) \quad or \quad (\phi_r<-70^{°} \quad and \quad -tan\alpha cosAz^{s}_{r} > tan(\pi/2+\phi_r)))
(
ϕ
r
>
7
0
°
a
n
d
t
a
n
α
c
o
s
A
z
r
s
>
t
a
n
(
π
/
2
−
ϕ
r
)
)
o
r
(
ϕ
r
<
−
7
0
°
a
n
d
−
t
a
n
α
c
o
s
A
z
r
s
>
t
a
n
(
π
/
2
+
ϕ
r
)
)
)
λ
i
p
p
=
λ
r
+
π
−
a
r
c
s
i
n
s
i
n
α
s
i
n
A
z
r
s
c
o
s
ϕ
i
p
p
\lambda_{ipp}=\lambda_r + \pi – arcsin\frac{sin\alpha sinAz^{s}_{r}}{cos\phi_{ipp}}
λ
i
p
p
=
λ
r
+
π
−
a
r
c
s
i
n
c
o
s
ϕ
i
p
p
s
i
n
α
s
i
n
A
z
r
s
(
o
t
h
e
r
w
i
s
e
)
(otherwise)
(
o
t
h
e
r
w
i
s
e
)
λ
i
p
p
=
λ
r
+
π
+
a
r
c
s
i
n
s
i
n
α
s
i
n
A
z
r
s
c
o
s
ϕ
i
p
p
\lambda_{ipp}=\lambda_r+\pi + arcsin\frac{sin\alpha sinAz^{s}_{r}}{cos\phi_{ipp}}
λ
i
p
p
=
λ
r
+
π
+
a
r
c
s
i
n
c
o
s
ϕ
i
p
p
s
i
n
α
s
i
n
A
z
r
s
1.3 根据三角关系(方法二)计算穿刺点
直接根据接收机和卫星的xyz坐标,根据三角关系计算接收机-穿刺点的距离,求出穿刺点zyz坐标,再将其转到llh坐标。其原理主要为:
s
t
a
=
X
R
2
+
Y
R
2
+
Z
R
2
sta = \sqrt{
{X_{R}}^{2} + {Y_{R}}^{2} + {Z_{R}}^{2}}
s
t
a
=
X
R
2
+
Y
R
2
+
Z
R
2
e
s
=
X
S
2
+
Y
S
2
+
Z
S
2
es = \sqrt{
{X_{S}}^{2} + {Y_{S}}^{2} + {Z_{S}}^{2}}
e
s
=
X
S
2
+
Y
S
2
+
Z
S
2
s
s
=
(
X
R
−
X
S
)
2
+
(
Y
R
−
Y
S
)
2
+
(
Z
R
−
Z
S
)
2
ss = \sqrt{({X_{R}-X_{S})}^{2} + ({Y_{R}-Y_{S})}^{2} + ({Z_{R}-Z_{S})}^{2}}
s
s
=
(
X
R
−
X
S
)
2
+
(
Y
R
−
Y
S
)
2
+
(
Z
R
−
Z
S
)
2
s
c
a
l
e
=
s
t
a
∗
s
i
n
(
π
/
2
−
e
l
e
−
z
′
)
/
s
i
n
z
′
s
s
scale = \frac{sta * sin(\pi /2 – ele – z^{‘})/sinz^{‘}}{ss}
s
c
a
l
e
=
s
s
s
t
a
∗
s
i
n
(
π
/
2
−
e
l
e
−
z
′
)
/
s
i
n
z
′
(正弦定理)
对应高度角计算方法为:
c
o
s
e
l
e
=
s
s
2
+
s
t
a
2
−
e
s
2
2
∗
s
s
∗
s
t
a
cosele = \frac{ss^2+sta^2-es^2}{2 * ss * sta}
c
o
s
e
l
e
=
2
∗
s
s
∗
s
t
a
s
s
2
+
s
t
a
2
−
e
s
2
程序中对应部分为:
/* ---------------calculate ionospheric pierce point position -----------------
* calculate ionospheric pierce point position
* args : double *recpos_xyz I receiver position in xyz
*
* double *satpos_xyz I satellite position in xyz
*
* double SHELL_H I ionosphere effective height(m)
*
* double *ipp_llh O ipp position{lat,lon, height}
*
* double *zen_ele O zenith and (elevation+2/pi)
* return : none
* notes : from PANDA-FORTRAN 2022-05-05 by hr
*-----------------------------------------------------------------------------*/
extern double cal_ipp( double* recpos_xyz, double* satpos_xyz, double SHELL_H, double* ipp, double* zen_ele)
{
double ssLength, esLength, staHeight;
double cosE, elev, sinZ, zenith;
double dx, dy, dz;
double scale, staLayerLength;
double ipp_xyz[3] = {0};
dx = satpos_xyz[0] - recpos_xyz[0];
dy = satpos_xyz[1] - recpos_xyz[1];
dz = satpos_xyz[2] - recpos_xyz[2];
ssLength = sqrt(dx * dx + dy * dy + dz * dz);
esLength = sqrt(satpos_xyz[0] * satpos_xyz[0] + satpos_xyz[1] * satpos_xyz[1] + satpos_xyz[2] * satpos_xyz[2]);
staHeight = sqrt(recpos_xyz[0] * recpos_xyz[0] + recpos_xyz[1] * recpos_xyz[1] + recpos_xyz[2] * recpos_xyz[2]);
//COMPUTE OF COS OF ELEVATION IS GEOCCENTRIC FRAME
cosE = (ssLength * ssLength + staHeight * staHeight - esLength * esLength) / (2.0 * ssLength * staHeight);
//ELEV SHOULD BETWEEN(0, PI)
elev = acos(cosE);
//GEOCCENTRIC IPP ZENITH
double sinele = sin(elev);
double factor = staHeight / (staHeight + SHELL_H);
sinZ = sin(elev) * staHeight / (staHeight + SHELL_H);
zenith = asin(sinZ);
staLayerLength = staHeight * sin(PI - elev - zenith) / sinZ;
scale = staLayerLength / ssLength;
dx = (satpos_xyz[0] - recpos_xyz[0]) * scale;
dy = (satpos_xyz[1] - recpos_xyz[1]) * scale;
dz = (satpos_xyz[2] - recpos_xyz[2]) * scale;
ipp_xyz[0] = recpos_xyz[0] + dx;
ipp_xyz[1] = recpos_xyz[1] + dy;
ipp_xyz[2] = recpos_xyz[2] + dz;
ecef2pos(ipp_xyz, ipp);
zen_ele[0] = zenith;
zen_ele[1] = elev;
/* double sum = (zenith + elev) * R2D;
double ipp_lat = ipp[0] * R2D;
double ipp_lon = ipp[1] * R2D;*/
return 0;
}
再根据前述方法插值计算vtec
2. 关于两种不同方法计算穿刺点得到的高度角、穿刺点经纬度的差异
以auck站2014年002天10号卫星,自19950-33150s弧段内数据为例
:
此处,方法一计算结果记为
方法1
,方法二计算结果记为
方法2
。
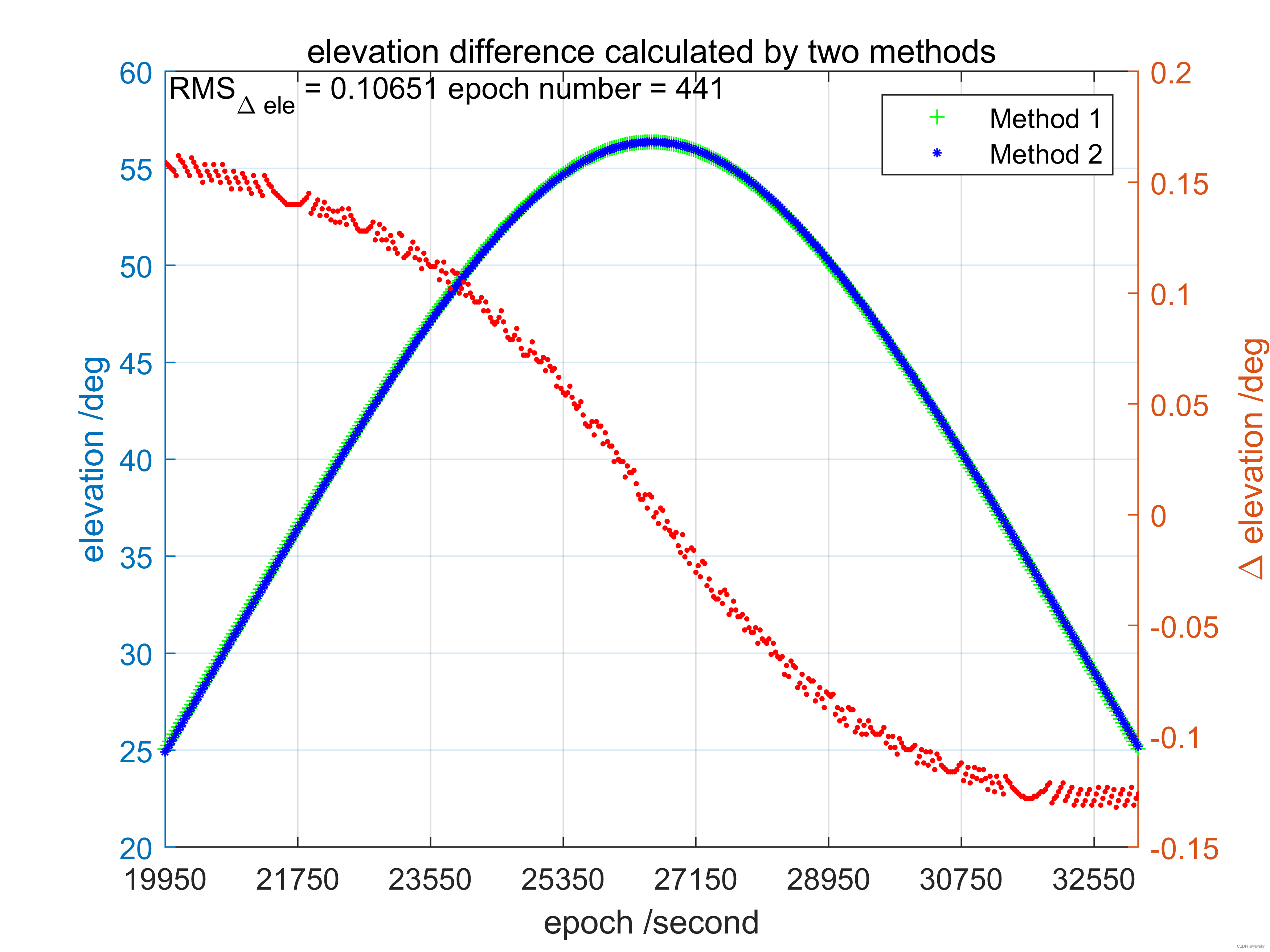
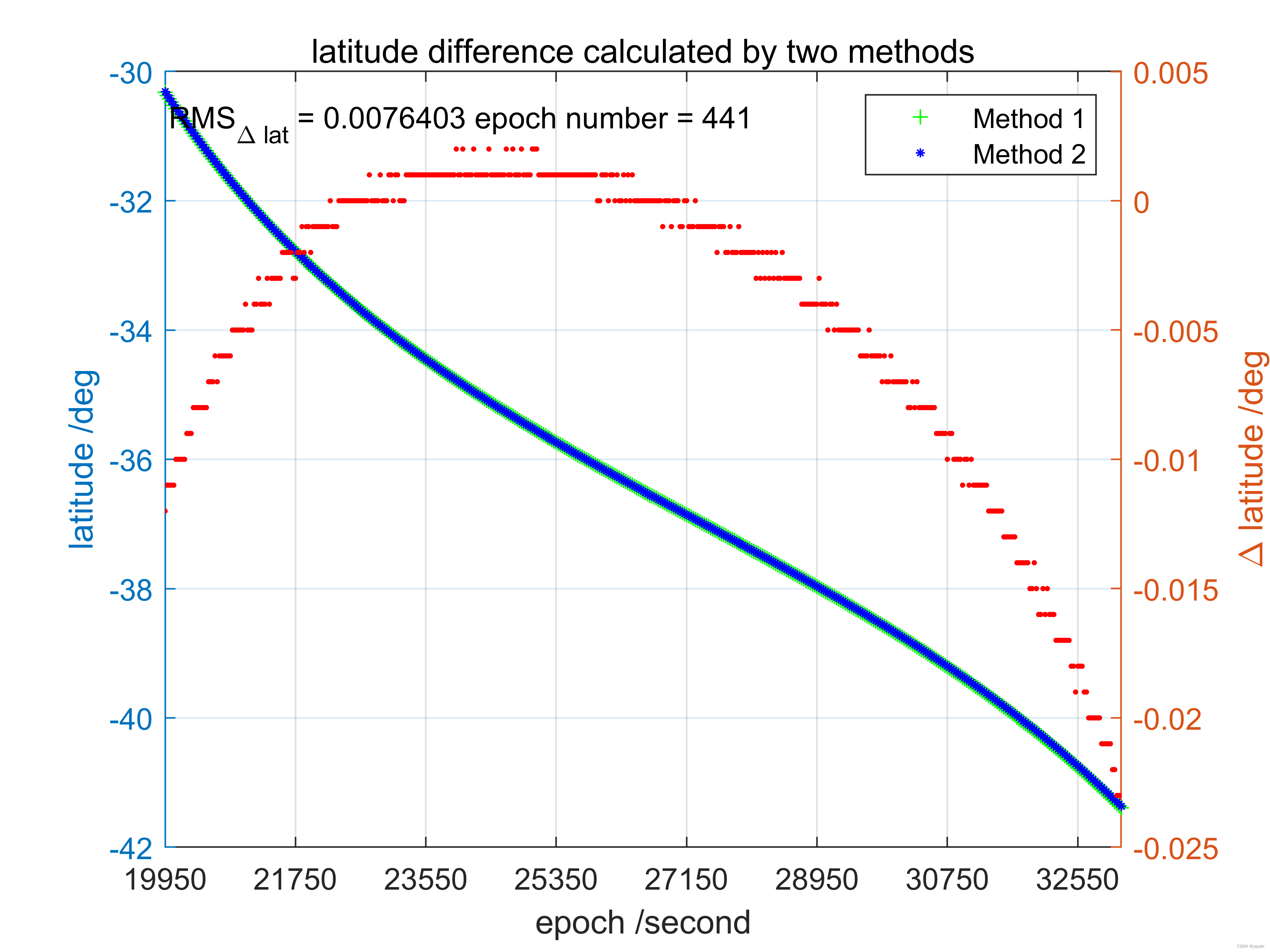
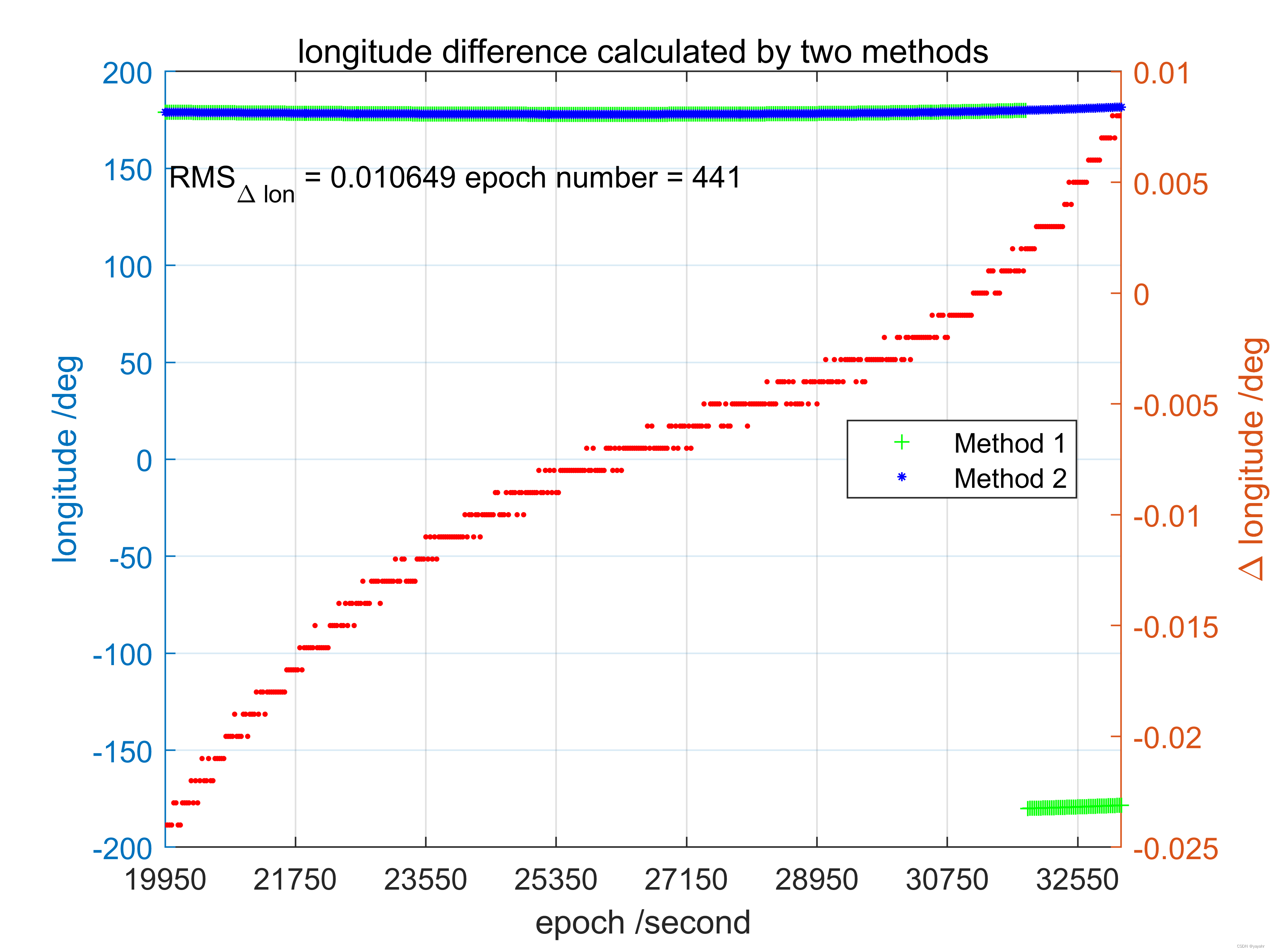
可以看出两种方法计算高度角差异rms在0.1°左右,经纬度计算差异rms值在0.01°以下,认为两种方法计算差异不大。
3. 计算VTEC考虑经度改正对结果的影响
3.1 根据穿刺点通过插值计算GIM 中VTEC方法
大部分程序中采用的方法为:分别计算当前时刻对应GIM和下一张GIM中VTEC,再通过时间长度进行线性插值:
E
(
β
,
λ
,
t
)
=
T
i
+
1
−
t
T
i
+
1
−
T
i
E
i
(
β
,
λ
)
+
t
−
T
i
T
i
+
1
−
T
i
E
i
+
1
(
β
,
λ
)
E(\beta,\lambda,t) = \frac{T_{i+1}-t}{T_{i+1}-T{i}}E_i(\beta,\lambda) + \frac{t – T_{i}}{T_{i+1}-T{i}}E_{i+1}(\beta,\lambda)
E
(
β
,
λ
,
t
)
=
T
i
+
1
−
T
i
T
i
+
1
−
t
E
i
(
β
,
λ
)
+
T
i
+
1
−
T
i
t
−
T
i
E
i
+
1
(
β
,
λ
)
其中,
β
,
λ
\beta,\lambda
β
,
λ
分别为穿刺点的纬度、经度,
t
t
t
为当前插值时刻,
E
i
(
β
,
λ
)
E_i(\beta,\lambda)
E
i
(
β
,
λ
)
表示第
i
i
i
幅GIM图中对应位置计算出的VTEC:
T
i
≤
t
≤
T
i
+
1
T_i\leq t\leq T_{i+1}
T
i
≤
t
≤
T
i
+
1
。
考虑到当前插值时间在两幅GIM图时间间隔内,在计算VTEC时,也需要考虑其和太阳的相对位置变化,即需要对插值计算时穿刺点的经度进行改正:
E
(
β
,
λ
,
t
)
=
T
i
+
1
−
t
T
i
+
1
−
T
i
E
i
(
β
,
λ
i
′
)
+
t
−
T
i
T
i
+
1
−
T
i
E
i
+
1
(
β
,
λ
i
+
1
′
)
E(\beta,\lambda,t) = \frac{T_{i+1}-t}{T_{i+1}-T{i}}E_i(\beta,\lambda^{‘}_{i}) + \frac{t – T_{i}}{T_{i+1}-T{i}}E_{i+1}(\beta,\lambda^{‘}_{i+1})
E
(
β
,
λ
,
t
)
=
T
i
+
1
−
T
i
T
i
+
1
−
t
E
i
(
β
,
λ
i
′
)
+
T
i
+
1
−
T
i
t
−
T
i
E
i
+
1
(
β
,
λ
i
+
1
′
)
其中,
λ
i
′
=
λ
+
(
t
−
T
i
)
\lambda^{‘}_{i}=\lambda+(t-T_i)
λ
i
′
=
λ
+
(
t
−
T
i
)
。
3.2 两种方法计算VTEC的造成的差异
此处,
仍以auck站2014年002天10号卫星,自19950-33150s弧段内数据为例
,不考虑和考虑旋转改正分别记为
NoRotaCorr
和
WithRotaCorr
。


可以发现当考虑经度改正时,在一个连续弧段内计算得到的VTEC出现了不连续的情况,如STEC差异图中的小图所示,不考虑经度改正时,计算得到的STEC连续,而考虑经度改正后在21990时刻出现约0.6TECu大小的跳动。经分析主要原因如下(以10号卫星在21960、21990、22020三个历元为例):
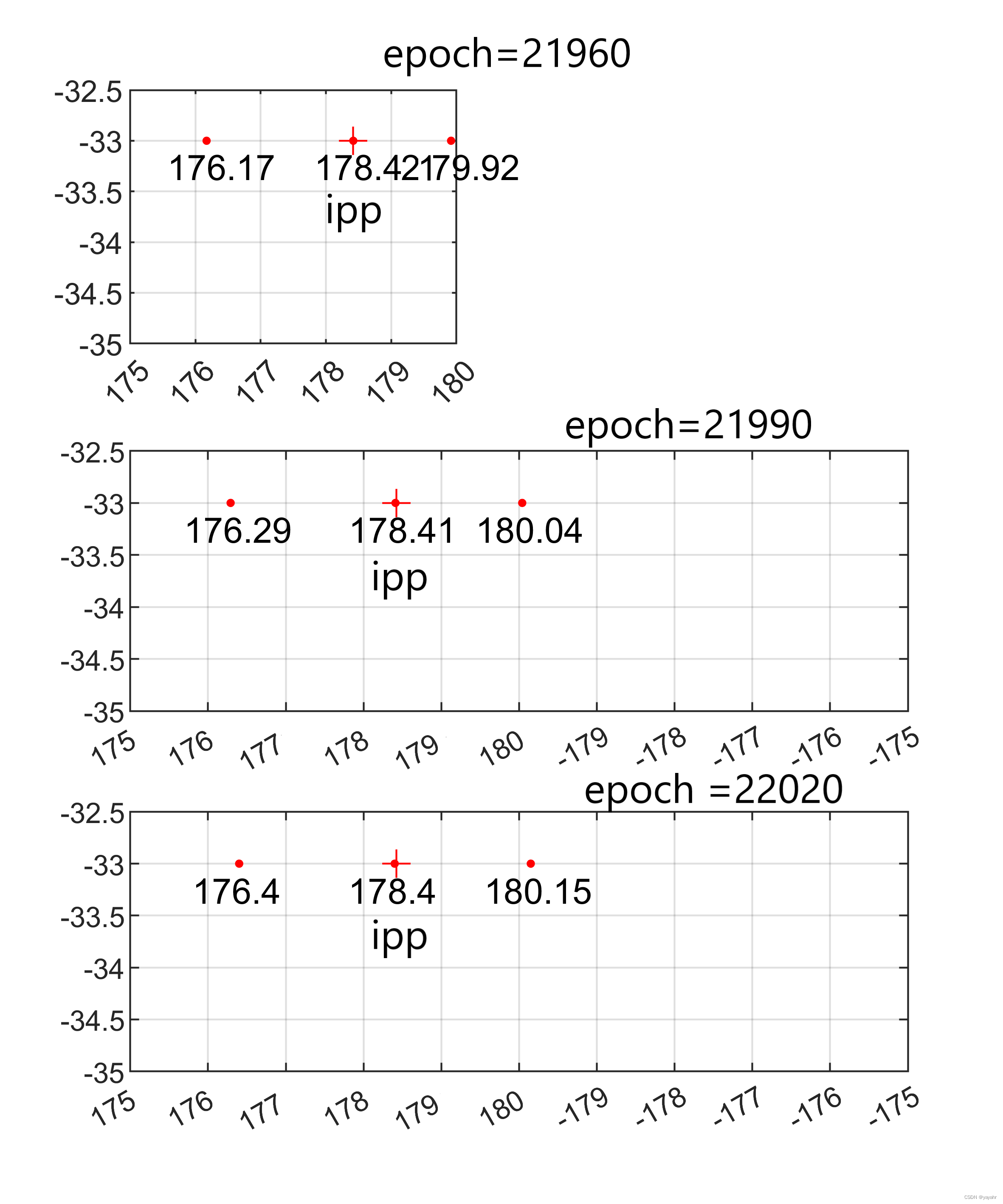
在21990时刻,
λ
=
178.41
\lambda = 178.41
λ
=
1
7
8
.
4
1
,考虑经度改正后
λ
i
′
\lambda^{‘}_{i}
λ
i
′
和
λ
i
+
1
′
\lambda^{‘}_{i+1}
λ
i
+
1
′
分别为180.04和176.29,此时
λ
i
′
\lambda^{‘}_{i}
λ
i
′
已经超出了该穿刺点对应格网的范围,即采用经度改正后的穿刺点计算的VTEC为相邻格网的数据,故此时计算出的VTEC最终结果与前一历元相比出现较大跳动。