1.名词解释 dB (分贝)
dB是一个比值,是一个数值,是一个纯计数方法,没有任何单位标注。
在不同领域有着不同的名称,因此它也代表不同的实际意义。
dB在电子学等领域中是一个很常用的单位。这个单位的特点在于使用对数,对原始数据进行表示。
1贝 = 10分贝 = 10dB
对于一个放大器:
功率放大倍数 Ap = 10 lg(Po/Pi)
电压放大倍数 Au = 20 lg(Uo/Ui)
电流放大倍数 Ai = 20 lg(Io/Ii)
例如:放大器放大倍率为40dB,说明其电压放大为100倍,电流放大也为100倍,故功率放大为10000倍.
2.数据取对数的意义
-
缩小数据的绝对数值,方便计算。
例如,每个数据项的值都很大,许多这样的值进行计算可能对超过常用数据类型的取值范围,这时取对数,就把数值缩小了。 -
取对数后,可以将乘法计算转换成加法计算。
例如,对于一个级联放大器,三级的功率放大倍率分别为10,100,1000,总倍率则为三者乘机,很容易计算和书写出错。但表示成dB形式,分别为10dB,20dB,30dB,总放大倍率为10+20+30=60dB,方便了很多。 -
某些情况下,在数据的整个值域中的在不同区间的差异带来的影响不同。
例如,从log函数的图像可以看到,自变量x的值越小,函数值y的变化越快,同样是相差300的两对数字,log500-log200>log800-log500,也就是说,对数值小的部分差异的敏感程度比数值大的部分的差异敏感程度更高。
这也是符合生活常识的,例如对于价格,买个家电,如果价格相差几百元能够很大程度影响你决策,但是你买汽车时相差几百元你会忽略不计了。 -
取对数之后不会改变数据的性质和相关关系,但压缩了变量的尺度。
例如800/200=4,但log800/log200=1.2616,数据更加平稳,也消弱了模型的共线性、异方差性等。
3.dBm与dBmV单位换算

4.dBm与W换算
dBm是一个表示功率绝对值的值(也可以认为是以1mW功率为基准的一个比值),计算公式为:10log(功率值/1mw)。
将dBm转换为W的口算规律是要先记住“1个基准”和“2个原则”:
-
“1个基准”:
30dBm=1W -
“2个原则”:
1)+3dBm,功率乘2倍;-3dBm,功率乘1/2
举例:33dBm=30dBm+3dBm=1W×2=2W
27dBm=30dBm-3dBm=1W×1/2=0.5W
2)+10dBm,功率乘10倍;-10dBm,功率乘1/10
举例:40dBm=30dBm+10dBm=1W×10=10W
20dBm=30dBm-10dBm=1W×0.1=0.1W
以上可以简单的记作:30是基准,等于1W整,互换不算难,口算可完成。加3乘以2,加10乘以10;减3除以2,减10除以10。
例1:44dBm=?W
44dBm=30dBm+10dBm+10dBm-3dBm-3dBm
=1W×10×10×1/2×1/2
=25W
例2:32dBm=?W
32dBm=30dBm+3dBm+3dBm+3dBm+3dBm-10dBm
=1W×2×2×2×2×0.1
=1.6W
计算技巧:
+1dBm和+2dBm的计算技巧
-
+1dBm=+10dBm-3dBm-3dBm-3dBm
=X×10×1/2×1/2×1/2
=X×1.25 -
+2dBm=-10dBm+3dBm+3dBm+3dBm+3dBm
=X×0.1×2×2×2×2
=X×1.6
在计算中,有时候也可以根据上面的规律变换为-1dBm和-2dBm,达到快速口速的目的,即:
-
-1dBm=-10dBm+3dBm+3dBm+3dBm
=X×0.1×2×2×2
=X×0.8 -
-2dBm=-3dBm+1dBm
=X×1/2×1.25
=X×0.625
例3:51dBm=30dBm+10dBm+10dBm+1dBm
=1W×10×10×1.25
=125W
例4:38dBm=30dBm+10dBm-2dBm
=1W×10×0.625
=6.25W
4. dBw与W的换算
dBw与dBm一样,dBw是一个表示功率绝对值的单位(也可以认为是以1W功率为基准的一个比值
),计算公式为:10log(功率值/1w)。
dBw与dBm之间的换算关系为:0 dBw = 10log1 W = 10log1000 mw = 30 dBm。
如果功率P为1W,折算为dBw后为0dBw。
5. 天线增益与dBi/dBd
通常所说的天线发射或接收信号的能力是用参照全向天线的分贝数来表示的,比如说天线增益有10dBi(10lg(10))不是说这副天线能把信号的功率放大10倍,而是通过控制信号发射的角度,将功率集中到一定的方向上。
**在输入功率相等的情况下,天线增益是指实际天线和全向天线在空间同一点处的功率密度之比,描述的是天线将功率集中辐射的程度,因此与天线方向图密切相关。**一般来说天线方向图主瓣越窄、副瓣越小,则增益越高。
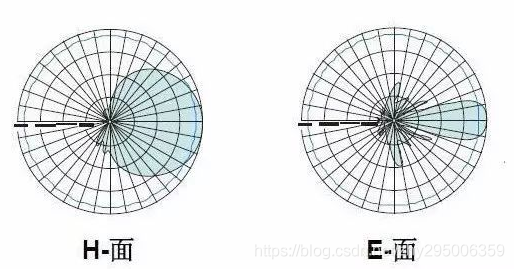
从天线方向图可以看出在空间不同方向有大小不同的增益,天线增益通常是指产生最大增益方向上的增益,单位为dBi或者dBd。这二个单位的参考基准不同,前者是以全方向性天线为基准,后者是以偶极子天线为基准。
在一定的距离上的某点处产生一定大小的信号,用理想的全向天线,假设需要100W的输入功率,而如果改用增益为G=20dBi的某定向天线作为发射天线,输入功率只需100 / ( 10^(20/10) )=1W。
偶极子天线的增益为G=0dBd=2.15dBi。
如果你经常听到有人说天线增益是多少多少dB,其实这是不严谨的,如果听到就当是dBi吧,但是要知道这和说放大器增益多少多少dB完全是不同的概念。
6. dBc
有时候我们也会看到dBc的单位,一般这是相对于载波功率来说的,用以度量和载波功率的相对值,例如同频/互调/交条/带外干扰或杂散等相对量值。
参考文献
1: dB、dBm、dBw和w的换算关系.
2: dBmv,dBm ,W 单位换算.
2: dBi介绍等.