写在前面
博主是23届一战上岸东南大学的考生。专业课920(信号与系统+数字电路)135分。给大家分享一下专业课的笔记,希望能帮到大家。
第一章绪论
1.1信号传输系统
信息传输的任务
将带有信息的信号,通过某种系统由发送者传送给接收者。
通信系统的组成
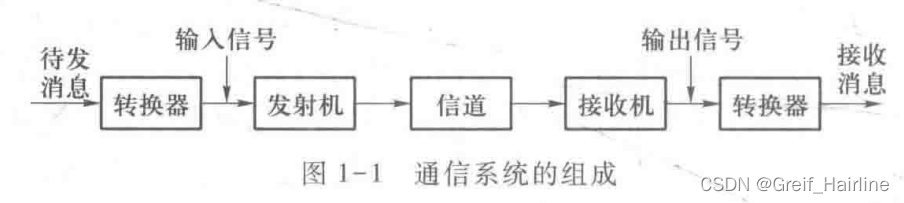
转换器:把消息转换为电信号或者把电信号还原成消息
信道:信号传输的通道,广义上来说。发射机和接收机也可以是信道的一部分
发射机 :把电信号转换成适合传输的大功率射频信号
接收机: 把发射机发射的信号转换成电信号
1.2信号的概念
定义
随着时间变化的物理量。更广义的说,万物皆可为信号。
描述
- 时域法
- 频域法(变换域)
分类
确定与随机信号
- 确定信号:可用确定的时间函数表示
- 随机信号:不可用确定的时间函数表示,只能用统计特性描述
- 联系: 确定信号是一种近似的、理想化的随机信号
连续与离散信号
- 连续信号:时间变量是连续的
- 离散信号:时间变量取离散值
- 数字信号:时间和幅度上都是离散的
- 模拟信号:时间和幅度上都是连续的
周期与非周期信号
- 绝对的周期信号不存在,工程上的周期信号指在较长时间内满足周期性
- 两个周期信号相加/相乘不一定是周期信号
- 连续周期信号抽样后不一定是周期信号(抽样后的离散信号的周期等于整数才可以)
- 因果周期信号不是周期信号如sintε(t),但是是功率信号
能量与功率信号
定义
- 能量信号:信号能量为非零有限值,功率为0
- 功率信号:信号平均功率为非零有限值,能量为无穷
- 非功非能信号:能量和功率都为无限值即为非功非能信号(典型信号:tε(t))
计算
1.能量计算
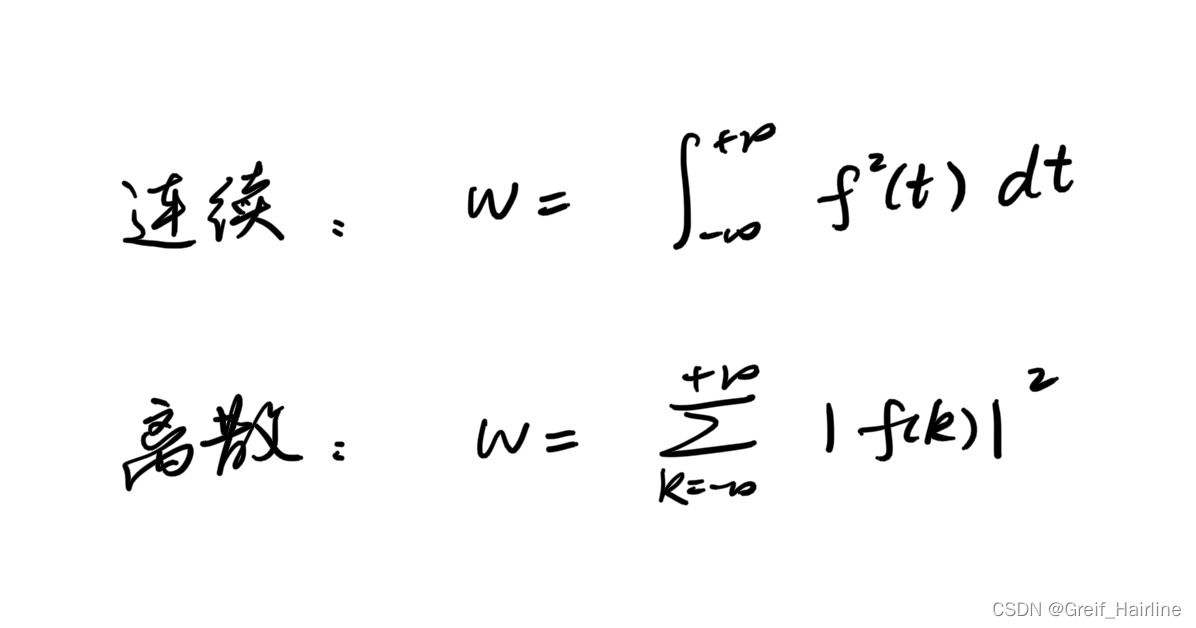
2.功率计算
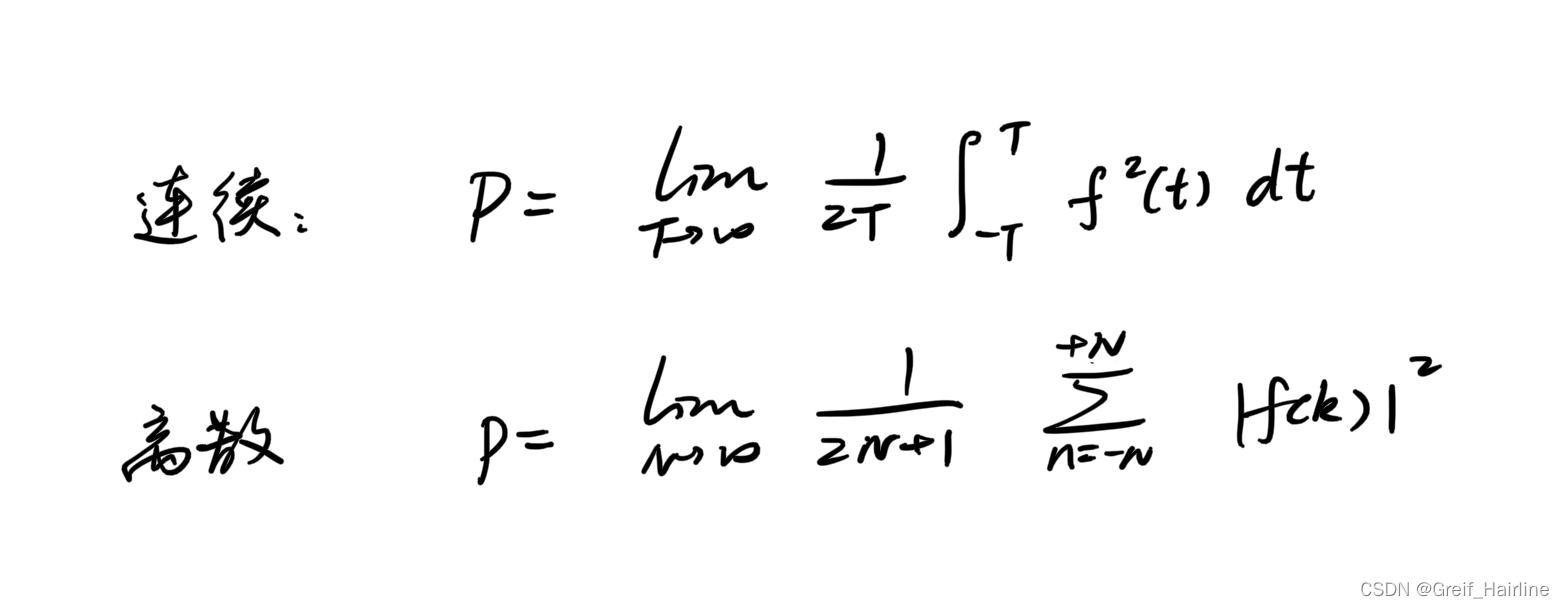
注意点
- 周期信号/周期信号的线性叠加一定是功率信号,非周期信号也有可能是功率信号
- 能量信号一定是非周期信号
- 有限时间信号一定是能量信号
- 因果周期信号也是功率信号如sintε(t)
- 以下说法是错误的
两个功率信号之和/积为功率信号(存在抵消的情况)
能量信号与功率信号乘积必为能量信号
随机信号必然是非周期信号
1.3信号的简单处理
注意:所有的变换针对自变量而言
- 叠加
- 相乘
- 平移(延时)
- 反褶
- 尺度变换
1.4系统的概念
定义
由若干互有关联的单元组成的、具有某种功能、用来达到某些特定目标的有机整体
描述方法
- 输入输出方程
- 框图模型
- 系统函数
- 状态方程
分类
线性和非线性系统
线性系统
定义:同时符合线性性和叠加性的系统
注意点:积分和微分都是线性运算
非线性系统
定义:不符合线性性和叠加性的系统
判定方法
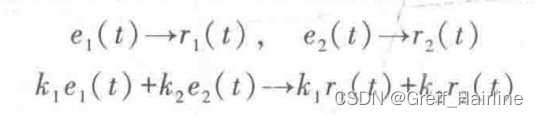
描述方法
线性系统可用线性微分方程或差分方程描述;非线性系统可用非线性微分方程或差分方程描述
非时变和时变系统
定义
非时变系统:系统性质不随时间变化,系统由定常参数元件构成
时变系统:系统性质随时间发生变化
判定方法
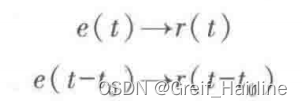
描述方法
非时变系统可用常系数线性微分方程来描述
连续时间和离散时间系统
连续时间系统:处理连续时间信号的系统
离散时间系统:处理离散时间信号的系统
因果和非因果系统
因果系统:符合因果规律的系统,即系统响应不可能出现在施加激励之前
非因果系统:不符合因果规律的系统
稳定和非稳定系统
稳定系统:在有限激励下产生有限响应的系统
非稳定系统:不满足上述条件的系统
1.5线性非时变系统的分析
系统的研究内容
分析:已知系统特性和激励信号,求系统输出
识别:已知输入和输出信号,求系统特性
设计:已知输入和目标输出信号,构造系统
系统分析的步骤
1.建立数学模型
2.进行分析
3.物理解释
系统分析方法
LTI连续时间系统
时域法
经典法:微分方程(直接法)
算子法:近代时域法和卷积法
变换域法
频域法:傅里叶变换
复频域法:拉普拉斯变换
状态方程法
LTI离散时间系统
时域法
经典法
算子法
变换域法:Z变换
状态方程法