本节介绍二阶系统的时域分析,主要介绍欠阻尼情况下的时间响应与动态性能指标
概述
二阶系统时间响应比较重要,因为所有高阶系统都可以使用二阶系统来近似。
二阶微分方程描述的系统称为二阶系统。反映在传递函数上就是闭环传递函数分母为s的2次方程。
二阶系统传递函数的标准形式
典型结构为一个惯性环节和一个积分环节串联


G
(
s
)
=
ω
n
2
s
(
s
+
2
ξ
ω
n
)
G(s)=\displaystyle \frac{\omega_n^2}{_{s(s+2\xi \omega_n)}}
G
(
s
)
=
s
(
s
+
2
ξ
ω
n
)
ω
n
2
Φ
(
s
)
=
ω
n
2
s
2
+
2
ξ
ω
n
s
+
ω
n
2
\Phi(s)=\displaystyle \frac{\omega_n^2}{_{s^2+2\xi \omega_ns+\omega_n^2}}
Φ
(
s
)
=
s
2
+
2
ξ
ω
n
s
+
ω
n
2
ω
n
2
其中
ω
n
\omega_n
ω
n
具有
1
时间
\frac{1}{
{时间}}
时间
1
的量纲,称为
自然频率
ξ
\xi
ξ
是常数,称为
阻尼比
或者
阻尼系数
二阶系统分类:
D
(
s
)
=
s
2
+
2
ξ
ω
n
s
+
ω
n
2
=
0
D(s)=s^2+2\xi \omega_ns+\omega_n^2=0
D
(
s
)
=
s
2
+
2
ξ
ω
n
s
+
ω
n
2
=
0
| 阻尼比 | 系统分类 | 特征根 |
|---|---|---|
|
ξ = 0 \xi=0 ξ = 0 |
0阻尼 |
λ 1 , 2 = ± j ω n \lambda_{1,2}=\pm j\omega_n λ 1 , 2 = ± j ω n |
|
0 < ξ < 1 0<\xi<1 0 < ξ < 1 |
欠阻尼 |
λ 1 , 2 = − ξ ω n ± j 1 − ξ 2 ω n \lambda_{1,2}=-\xi \omega_n \pm j\sqrt{1-\xi^2} \omega_n λ 1 , 2 = − ξ ω n ± j 1 − ξ 2 ω n |
|
ξ = 1 \xi=1 ξ = 1 |
临界阻尼 |
λ 1 = λ 2 = − ω n \lambda_{1}=\lambda_2=-\omega_n λ 1 = λ 2 = − ω n |
|
ξ > 1 \xi>1 ξ > 1 |
过阻尼 |
λ 1 , 2 = − ξ ω n ± ξ 2 − 1 ω n \lambda_{1,2}=-\xi \omega_n\pm \sqrt{\xi^2-1}\omega_n λ 1 , 2 = − ξ ω n ± ξ 2 − 1 ω n |
−
1
<
ξ
<
0
-1<\xi<0
−
1
<
ξ
<
0
,系统震荡发散,
ξ
<
−
1
\xi<-1
ξ
<
−
1
,系统单调发散。不稳定,所以不加讨论。
极点的表示方法
特征根,也就是系统的极点,有以下几种不同的表示方法:
-
直角座标表示
λ1
,
2
=
−
ξ
ω
n
±
j
1
−
ξ
2
ω
n
\lambda_{1,2}=-\xi \omega_n \pm j\sqrt{1-\xi^2}\omega_n
λ
1
,
2
=
−
ξ
ω
n
±
j
1
−
ξ
2
ω
n
其虚部
ωd
=
ω
n
1
−
ξ
2
\omega_d=\omega_n\sqrt{1-\xi^2}
ω
d
=
ω
n
1
−
ξ
2
称为
阻尼震荡频率
-
“极”座标表示
注意,这个不是真的极座标,只是用极座标的方式去理解
把
λ\lambda
λ
写成模值+相角的形式
{∣
λ
∣
=
ω
n
∠
λ
=
β
\left \{ \begin{aligned} |\lambda|&=\omega_n\\ \angle \lambda&=\beta \end{aligned} \right.
{
∣
λ
∣
∠
λ
=
ω
n
=
β

根据几何关系:
{cos
β
=
ξ
sin
β
=
1
−
ξ
2
\left \{ \begin{aligned} \cos \beta&=\xi\\ \sin \beta&=\sqrt {1-\xi^2} \end{aligned} \right.
{
cos
β
sin
β
=
ξ
=
1
−
ξ
2
β\beta
β
角也称
阻尼角
无阻尼响应
此时特征根为共轭纯虚根


临界阻尼响应
此时特征根为两个相同的负实根


没有超调。
调节时间
t
s
≈
4.7
1
ω
n
t_s\approx4.7\frac{1}{\omega_n}
t
s
≈
4.7
ω
n
1
响应时间比过阻尼快。
过阻尼响应
此时特征根为两个不同的负实根

过阻尼情况下时间响应增加比临界阻尼更慢。
过阻尼情况可以等效为两个一阶惯性系统的串联。如果两个特征根绝对值相差很大(3倍以上),则这个二阶系统可以近似用一阶系统来表示。
动态性能指标的计算:
定义时间常数:
T
1
,
2
=
1
ω
n
(
ξ
±
ξ
2
−
1
)
T_{1,2}=\frac{1}{\omega_n(\xi \pm \sqrt{\xi^2-1})}
T
1
,
2
=
ω
n
(
ξ
±
ξ
2
−
1
)
1
系统时间响应:
y
(
t
)
=
1
+
e
−
t
/
T
1
T
2
/
T
1
−
1
+
e
−
t
/
T
2
T
1
/
T
2
−
1
y(t)=1+\frac{e^{-t/T_1}}{T_2/T_1-1}+\frac{e^{-t/T_2}}{T_1/T_2-1}
y
(
t
)
=
1
+
T
2
/
T
1
−
1
e
−
t
/
T
1
+
T
1
/
T
2
−
1
e
−
t
/
T
2
方程很难解,所以一般直接读图:

「图源:胡寿松-自动控制原理」
首先根据
T
1
T
2
\frac{T_1}{T_2}
T
2
T
1
或者
ξ
\xi
ξ
,在曲线上确定出一个点。然后读出这个点对应的
t
s
T
1
\frac{t_s}{T_1}
T
1
t
s
,结合T
1
的值就可以计算t
s
的值了。
通过一个例子来体会一下这个曲线怎么用:

在工程实践中,如果
ξ
≥
1.5
\xi \ge1.5
ξ
≥
1.5
,可以按照一阶系统计算:
t
s
=
(
3
∼
4
)
T
1
=
(
3
∼
4
)
×
1
(
ξ
−
ξ
2
−
1
)
ω
n
t_s=(3\sim4)T_1=(3\sim4)\times \displaystyle \frac{1}{(\xi-\sqrt{\xi^2-1})\omega_n}
t
s
=
(
3
∼
4
)
T
1
=
(
3
∼
4
)
×
(
ξ
−
ξ
2
−
1
)
ω
n
1
欠阻尼响应
此时特征根为共轭复根。
欠阻尼系统的单位阶跃响应


动态性能的三个结论:
{
t
p
=
π
1
−
ξ
2
⋅
ω
n
σ
=
e
−
ξ
π
1
−
ξ
2
t
S
≈
3.5
ξ
ω
n
\left \{ \begin{aligned} t_p&=\frac{\pi}{\sqrt{1-\xi^2}\cdot \omega_n}\\ \sigma&=e^{\frac{-\xi \pi}{\sqrt{1-\xi^2}}}\\ t_S&\approx\frac{3.5}{\xi \omega_n} \end{aligned} \right.
⎩
⎨
⎧
t
p
σ
t
S
=
1
−
ξ
2
⋅
ω
n
π
=
e
1
−
ξ
2
−
ξ
π
≈
ξ
ω
n
3.5
也有教材里面
t
s
≈
3
ξ
ω
n
(
5
%
误差带
)
,
4
ξ
ω
n
(
2
%
误差带
)
t_s\approx\frac{3}{\xi \omega_n}(5\%误差带),\frac{4}{\xi \omega_n}(2\%误差带)
t
s
≈
ξ
ω
n
3
(
5%
误差带
)
,
ξ
ω
n
4
(
2%
误差带
)

再补充几个不太重要的指标,了解即可:
上升时间:
t
r
=
π
−
β
ω
d
,
ω
d
=
ω
n
⋅
1
−
ξ
2
\displaystyle t_r=\frac{\pi -\beta}{\omega_d},\omega_d=\omega_n\cdot\sqrt{1-\xi^2}
t
r
=
ω
d
π
−
β
,
ω
d
=
ω
n
⋅
1
−
ξ
2
震荡次数:
N
=
1.5
1
−
ξ
2
π
ξ
N=\displaystyle \frac{1.5\sqrt{1-\xi^2}}{\pi \xi}
N
=
π
ξ
1.5
1
−
ξ
2
之前说性能指标的时候就已经说过,实际上使用的是单位阶跃响应曲线的包络线。
包络线
是曲线:
y
(
t
)
=
1
±
1
1
−
ξ
2
e
−
ξ
ω
n
t
y(t)=1\pm \frac{1}{\sqrt{1-\xi^2}}e^{-\xi\omega_nt}
y
(
t
)
=
1
±
1
−
ξ
2
1
e
−
ξ
ω
n
t
实际调节时间是不连续的,比如下面这种情况:(
ω
n
\omega_n
ω
n
为常数)

在
ξ
2
\xi_2
ξ
2
的情况下,第二次震荡刚好在误差带之内,所以计算调节之间只需要看第一次震荡进入误差带的时间t
2
就可以了。
但是在
ξ
1
\xi_1
ξ
1
的情况下,第二次震荡刚好超出了误差带,所以必须计算第三次震荡进入误差带的时间t
1
虽然
ξ
1
\xi_1
ξ
1
ξ
2
\xi_2
ξ
2
相差很少,但是反映在调节时间上就相差很大了。
最佳阻尼比
ξ=
0.707
\xi=0.707
ξ
=
0.707
刚好时间响应曲线与误差带相切。这样实际上的调节时间是最短的。
用极座标表示就是
β
=
45
°
\beta=45\degree
β
=
45°
最佳阻尼比下,系统的实际调节时间:
2
ξ
ω
n
\frac{2}{\xi \omega_n}
ξ
ω
n
2
动态性能与极点分布的关系

极点向上移动,超调量增大,但调节时间不变
向左移动,超调量减小,调节时间也减小
沿着某一条倾斜直线远离原点移动,超调量不变,调节时间减小
λ
1
,
2
=
−
ξ
ω
n
±
j
1
−
ξ
2
ω
n
\lambda_{1,2}=-\xi \omega_n \pm j\sqrt{1-\xi^2}\omega_n
λ
1
,
2
=
−
ξ
ω
n
±
j
1
−
ξ
2
ω
n
按照直角座标变化:向上即是仅虚部
1
−
ξ
2
ω
n
\sqrt{1-\xi^2}\omega_n
1
−
ξ
2
ω
n
增大,
β
\beta
β
角增大,对应
ξ
\xi
ξ
减小,
σ
=
e
−
ξ
π
/
1
−
ξ
2
\sigma=e^{-\xi \pi/\sqrt{1-\xi^2}}
σ
=
e
−
ξ
π
/
1
−
ξ
2
增大。
t
s
=
3.5
ξ
ω
n
t_s=\frac{3.5}{\xi \omega_n}
t
s
=
ξ
ω
n
3.5
不变。
向左即是仅实部
−
ξ
ω
n
-\xi \omega_n
−
ξ
ω
n
变小,
ξ
ω
n
\xi \omega_n
ξ
ω
n
变大。
β
\beta
β
角减小,对应
ξ
\xi
ξ
增大。同样代入公式:
σ
\sigma
σ
减小,
t
s
t_s
t
s
也减小。
按照极座标变化:
远离原点即是
ω
n
\omega_n
ω
n
变大,
β
\beta
β
角不变,
ξ
\xi
ξ
不变。代入公式,
t
s
t_s
t
s
减小,
σ
\sigma
σ
不变。
绕原点顺时针转动即是
ω
n
\omega_n
ω
n
不变,
β
\beta
β
角增大,
ξ
\xi
ξ
减小。代入公式,
t
s
t_s
t
s
增大,
σ
\sigma
σ
增大。
例题
欠阻尼二阶系统重点掌握动态性能指标的三个公式就可以了。

除了这种已知系统参数要求性能指标的题,还有已知性能指标倒求系统参数的题:

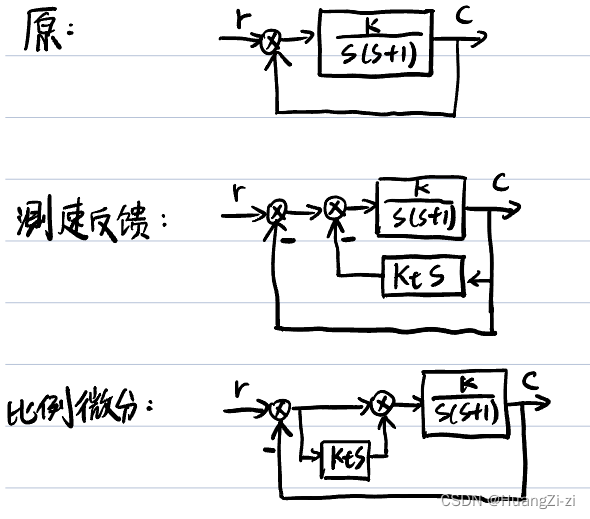
改善二阶系统动态性能的措施
- 测速反馈(增加阻尼)
-
比例+微分(提前控制)