相关系数
一,皮尔逊pearson相关系数
1 pearson相关系数使用条件和检验条件
1) 使用和检验条件
我们常说的相关系数指得就是皮尔逊(pearson)相关系数。
条件一:我们的样本数据必须满足
正态分布
。
条件二:样本数据是
连续
的且数据之间的差异不能太大(不能包含
离群点
或异常值)。
条件三:每组样本之间
相互独立
。
条件四:皮尔逊相关系数有效的前提是两组数据(两个对象)之间呈
线性关系
。
2) 散点图检验
使用EXCEL或者SPSS(对象很多)或者matlab
绘制散点图
来看是否存在线性关系,并看数据是否连续,有无离群点。
3) 正态分布检验
正态分布检验:
雅克‐贝拉检验
(Jarque‐Bera test) 和Shapiro‐wilk
夏皮洛‐威尔克检验
以及
Q-Q图
1)
JB检验
:MATLAB中进行JB检验的语法:[h,p] = jbtest(x,alpha)。
JB检验是大样本检验(
n>30
)
注解:
h返回0或1,1表示拒绝原假设,0表示接受原假设,且H0:该随机变量服从正态分布,H1:该随机变量不服从正态分布。
p返回P值。
x是数据向量。
alpha是显著性水平,一般0.05。
2)
Shapiro‐wilk检验
:Shapiro‐wilk检验是小样本检验(
3≤n≤50
)
SPSS
操作。分析->描述统计->探索->图->含检验的正态图。得到P值,P值<0.05表示拒绝原假设即随机变量不服从正态分布。
3)
Q-Q图
:要利用Q‐Q图鉴别样本数据是否近似于正态分布,只需看Q‐Q图上的点是否近似地在
一条直线
附近。(要求
数据量非常大
)
MATLAB函数
qqplot(x)
:x是数据向量。
2 pearson相关系数如何求?
MATLAB的
corrcoef
函数。
R = corrcoef(A)
返回 A 的相关系数的矩阵,其中 A 的列表示随机变量(指标),行表示观测值(样本)。
R = corrcoef(A,B)
返回两个随机变量 A 和 B (两个向量)之间的相关系数。
3 pearson相关系数假设性检验(显著性检验)
1)
MATLAB
一行代码:[R,P] =
corrcoef
(Test)
R返回的是相关系数表,P返回的是对应于每个相关系数的p值
p值小于0.05说明在95%置信水平上拒绝原假设即相关系数显著异于0。
2)
SPSS
也可生成相关系数表,并且有
显著性标记
步骤:分析->相关->双变量->皮尔逊
二,斯皮尔曼spearman等级相关系数
spearman等级相关系数的定义有两种,MATLAB使用的定义是:斯皮尔曼相关系数被定义成等级之间的皮尔逊相关系数。等级按照从小到大排序。
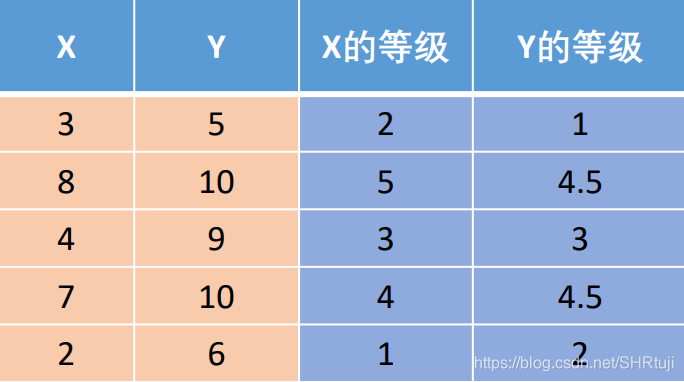
MATLAB使用函数:corr(X , Y , ‘type’ , ‘Spearman’)或corr(X , ‘type’ , ‘Spearman’)分别表示两个
列向量
的spearman等级相关系数和
X矩阵各列之间
的spearman等级相关系数。
1 spearman等级相关系数假设性检验(显著性检验)
分为
小样本
和
大样本
两种情况:
1)小样本
小样本情况,即? <=??时,直接查临界值表即可。
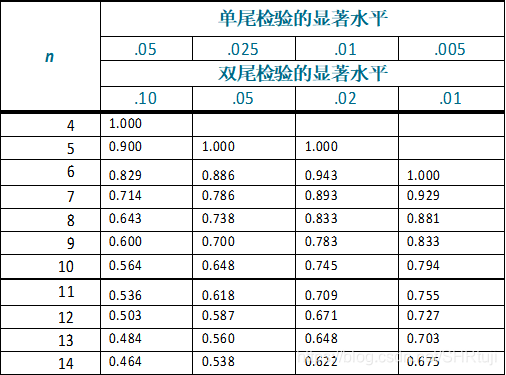
当相关系数
大于
临界值说明相关系数显著异于0即
显著相关
2)大样本
MATLAB函数[R,P]=corr(X, ‘type’ , ‘Spearman’) //直接给出P值
P值
小于
0.05则
拒绝原假设
即 相关系数 和 0 有显著性差异。
三,两种相关系数的选择
满足皮尔逊相关系数的
使用条件
和
检验条件
则使用皮尔逊相关系数。
只要其中一个条件不满足则使用斯皮尔曼等级相关系数。另外两个
定序数据
之间的相关系数求解也用斯皮尔曼。斯皮尔曼相关系数的适用条件比皮尔逊相关系数要广。
//定序数据:其反映在某一指标下观测对象的等级,排名,优劣等,可用数字和文字表示,但不能参与运算,所以只能用斯皮尔曼等级相关系数。
学数学建模可关注B站的清风数学建模,是个较好的途经去了解学习数学建模(亲测)。