马氏链
原理

采样方法
所谓的采样方法,主要就是利用了马氏链的性质
π
n
(
x
)
\pi_n(x)
π
n
(
x
)
为一个离散的概率分布
π
n
(
x
)
=
[
π
n
(
1
)
,
π
n
(
2
)
,
.
.
.
,
π
n
(
m
)
]
\pi_n(x)=[\pi_n(1),\pi_n(2),…,\pi_n(m)]
π
n
(
x
)
=
[
π
n
(
1
)
,
π
n
(
2
)
,
.
.
.
,
π
n
(
m
)
]
当马氏链收敛至平稳分布时(假设第n次转移时收敛),
π
n
(
x
)
,
π
n
+
1
(
x
)
,
π
n
+
2
(
x
)
,
.
.
.
.
\pi_n(x),\pi_{n+1}(x),\pi_{n+2}(x),….
π
n
(
x
)
,
π
n
+
1
(
x
)
,
π
n
+
2
(
x
)
,
.
.
.
.
这些概率分布都是相等的
若随机变量
X
0
∼
π
0
(
x
)
X_0 \sim \pi_0(x)
X
0
∼
π
0
(
x
)
,
X
1
∼
π
1
(
x
)
X_1 \sim \pi_1(x)
X
1
∼
π
1
(
x
)
,…,
X
n
∼
π
n
(
x
)
X_n \sim \pi_n(x)
X
n
∼
π
n
(
x
)
,
X
n
+
1
∼
π
n
+
1
(
x
)
X_{n+1} \sim \pi_{n+1}(x)
X
n
+
1
∼
π
n
+
1
(
x
)
那么这些随机变量
X
n
∼
π
n
(
x
)
X_n \sim \pi_n(x)
X
n
∼
π
n
(
x
)
,
X
n
+
1
∼
π
n
+
1
(
x
)
X_{n+1} \sim \pi_{n+1}(x)
X
n
+
1
∼
π
n
+
1
(
x
)
,…都是服从同一个分布的
对于一个具体的状态,
即一个具体的值
x
i
x_i
x
i
而非随机变量
,从
x
n
x_n
x
n
开始的一系列这样的值
x
n
,
x
n
+
1
,
x
n
+
2
.
.
.
x_n,x_{n+1},x_{n+2}…
x
n
,
x
n
+
1
,
x
n
+
2
.
.
.
就是服从同一个分布
π
(
x
)
=
π
n
(
x
)
\pi(x)=\pi_n(x)
π
(
x
)
=
π
n
(
x
)
的样本点,我们通过这种方式可以
生成某个分布的大量的随机样本点
,这就是传说中的
采样
MH采样
原理

代码
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
np.random.seed(42)
# 正态分布
x_=np.linspace(-20,20,100)
y_=stats.norm.pdf(x_,0,5)# 正态分布
# y_=stats.expon(scale=1).pdf(x_)# 指数分布
# 采样数10000
Samp_Num=10000
result=[]
init=1
result.append(init)
# p=lambda r:stats.expon(scale=1).pdf(r)# 指数分布
p=lambda r:stats.norm.pdf(r,0,5) # 正态分布
# 生成均值为v,标准差为2的正态分布的1个样本
q=lambda v:stats.norm.rvs(loc = v,scale = 2, size = 1)
for i in range(Samp_Num):
y=q(result[i])# 从分布q(y|x_t)中随机采样一个样本点
alpha=min(1,p(y)/p(result[i]))# 接受概率(简化)
u=np.random.rand(1)# 从uniform(0,1)中采样
if u<alpha:
result.append(y[0])# 接受
else:
result.append(result[i])# 拒绝
if i%1000==0:
print(i)
plt.hist(result, 50, density=1, facecolor='blue', alpha=0.5)
plt.plot(x,raw_y)
plt.show()
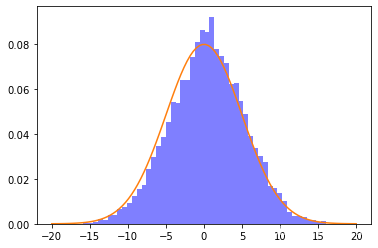
下图为利用MH采样法拟合的高斯分布
Gibbs采样
原理
Gibbs采样是高维采样的推广,用以
生成高维联合概率分布的样本点

代码
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
def p_x_given_y(y, mus, sigmas):
mu = mus[0] + sigmas[1, 0] / sigmas[0, 0] * (y - mus[1])
sigma = sigmas[0, 0] - sigmas[1, 0] / sigmas[1, 1] * sigmas[1, 0]
return np.random.normal(mu, sigma)
def p_y_given_x(x, mus, sigmas):
mu = mus[1] + sigmas[0, 1] / sigmas[1, 1] * (x - mus[0])
sigma = sigmas[1, 1] - sigmas[0, 1] / sigmas[0, 0] * sigmas[0, 1]
return np.random.normal(mu, sigma)
def gibbs_sampling(mus, sigmas, iter=10000):
samples = np.zeros((iter, 2))
y = np.random.rand() * 10
for i in range(iter):
x = p_x_given_y(y, mus, sigmas)
y = p_y_given_x(x, mus, sigmas)
samples[i, :] = [x, y]
return samples
mus = np.array([5, 5])
sigmas = np.array([[1, .9], [.9, 1]])
x,y = np.random.multivariate_normal(mus, sigmas, int(1e5)).T
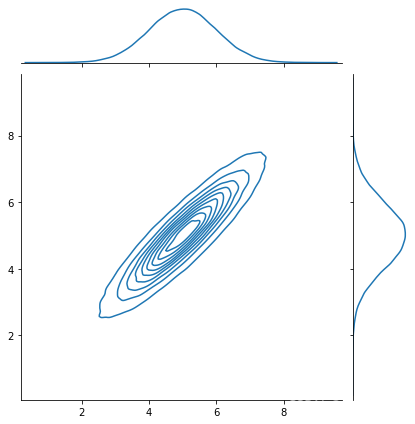
sns.jointplot(x,y,kind='kde')
下图为生成的联合高斯分布图
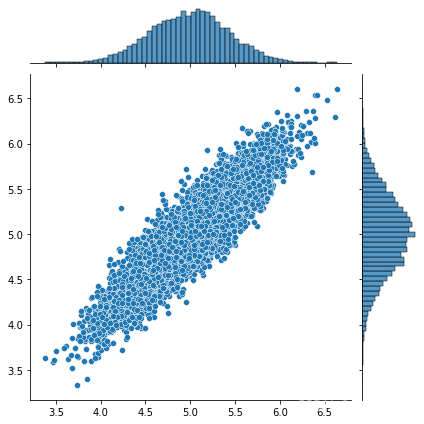
samples = gibbs_sampling(mus, sigmas)
sns.jointplot(samples[:, 0], samples[:, 1])
下图为Gibbs采样得到的分布图