创建名为 prac08.py 的文件,在文件中定义两个类,一个是顶点的结点类,另一个 是图类,该类包含存储连通网的邻接矩阵、广度优先遍历图的方法和求连通网的最小生成树 的方法。请按以下步骤实现连通网的最小生成树算法。
-
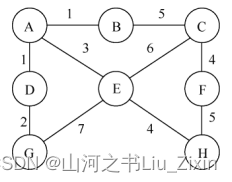
创建一个下图所示的无向网,并使用数组表示法存储它。
-
广度优先遍历该网,判断该网是否连通。
-
使用 Prim 算法构造该网的最小生成树,并将构造过程输出。
-
使用 Kruskal 算法构造该网的最小生成树,并将构造过程输出。
-
比较3和4中构造最小生成树的过程,深入理解 Prim 算法和 Kruskal 算法构造连 通网的最小生成树的差异。
(注:本文所使用的图的写入方法是根据连接作图,也就是无需提前构建节点,直接写连接,涉及到的节点将会自动导入,如上图可表示为:A1B,A3E,A1D等边,用边描述图)
class Vertex(object): # 节点类
def __init__(self, data):
self.data = data # 节点的data属性
class Graph(object): # 新建图
def __init__(self):
self.adjacency_matrix = [] # 邻接矩阵
self.vertex_set = [] # 节点集
self.vertex_counter = 0 # 看看有几个节点
def CreateGraph(self):
list_relation = [] # 临时存储边用的列表
list_vertex = [] # 临时存储节点用的列表
while True:
info = input("请输入一条连接,格式为A,n,B,A、B分别为相连的两个顶点,n为边的权值(或输入“终止”以结束):")
if info != "终止":
try:
relation = info.split(",") # 逗号分隔出两个节点和一个边
relation[1] = int(relation[1]) # 将中间的边的权值转换为数字
relation_reversed = list(reversed(relation)) # 将列表倒序
list_relation.append(relation_reversed) # 通过删除这行、上一行和下一行这三行可以实现转无向网到有向网,这算是编程的时候的意外收获
list_relation.append(relation) # 先后添加入正序和倒序的关系,每两个构成一个无向边(双向边)
except Exception as e: # 捕获异常(主要是防止输入错误之类的)
print(e)
else:
break # 终止
for i in range(len(list_relation)): # 将临时存储边的列表中的节点提取出来存入节点列表
list_vertex.append(list_relation[i][0])
list_vertex.append(list_relation[i][2])
list_vertex = list(set(list_vertex)) # 列表去重(不是最好的,但是代码量最小的)
list_vertex.sort() # 排序(便于下一步即使不用字典也可以轻松地实现两个列表之间的index对照)
for i in range(len(list_vertex)):
self.vertex_counter += 1 # 算节点数的,也可以直接用len
vertex = Vertex(list_vertex[i]) # 新建图节点
self.vertex_set.append(vertex) # 添加入节点集
self.adjacency_matrix = [[0 for j in range(self.vertex_counter)]for i in range(self.vertex_counter)] # 根据之前获得的节点数初始化邻接矩阵
for i in range(len(list_relation)): # 对每一个边写入邻接矩阵
index_j = 0
index_k = 0 # 两个用于把for循环中确定的节点位置取出来的参数
for j in range(len(list_vertex)): # 循环用于确定该边的起始节点是第几号节点,从而确定其位于邻接矩阵的第几行
if list_vertex[j] == list_relation[i][0]:
index_j = j
for k in range(len(list_vertex)): # 循环用于确定该边的终止节点是第几号节点,从而确定其位于邻接矩阵的第几列
if list_vertex[k] == list_relation[i][2]:
index_k = k
self.adjacency_matrix[index_j][index_k] = list_relation[i][1] # 按照获得的坐标写入权值
print("创建完成")
def BFS(self): # BFS算法锦星便利,并获取遍历结果
visited = ["0" for i in range(self.vertex_counter)] # 是否以访问的标签列表(这里就体现出之前排序的作用了)
queue = [[self.adjacency_matrix[0], 0]] # 队列,有点像二叉树的层次遍历,这里存有某个节点的全部连接信息以及这是第几个节点,初始化
while queue: # 是否为空(遍历是否完成)
cursor = queue.pop(0) # 出队
if visited[cursor[1]] == "0": # 如果之前没访问到就访问一下
visited[cursor[1]] = "1"
for i in range(len(self.adjacency_matrix)): # 遍历该节点的全部连接属性
if self.adjacency_matrix[cursor[1]][i] != 0 and visited[i] == "0": # 这个连接是否存在以及对应的另一端的节点是否已访问
queue.append([self.adjacency_matrix[i], i]) # 没有的话就写入准备访问
else:
continue
return visited # 返回访问结果,正常应该全为“1”,不可达的就会出现“0”
def Prim(self, vertex): # Prim算法
arc = [] # 用于存储生成树信息
close_edge = [[] for i in range(self.vertex_counter)] # 临边(最多也不过吧所有的连接一遍,也就是节点数-1)
min_edge = 0 # 最小边
index = 0 # 用于计数的索引
while index < self.vertex_counter: # 初始化close_edge
close_edge[index] = [vertex, self.adjacency_matrix[vertex][index]]
index = index + 1
index = 1 # 不能再赋0了,毕竟自己没法连接自己(在本情境下)
while index < self.vertex_counter:
min_edge = self.GetMin(close_edge) # 获取该条件下权值最小的边,将其处世界店,终止节点和权值存入arc
arc.append([self.vertex_set[close_edge[min_edge][0]].data, self.vertex_set[min_edge].data, self.adjacency_matrix[min_edge][close_edge[min_edge][0]]])
close_edge[min_edge][1] = 0
i = 0
while i < self.vertex_counter:
if self.adjacency_matrix[min_edge][i] < close_edge[i][1]: # close_edge需要更新,不然的话下一次还会访问到这个边
close_edge[i] = [min_edge, self.adjacency_matrix[min_edge][i]]
i += 1
index += 1
print("Prim算法构造的最小生成树的边如下:")
for i in arc:
print(i)
def GetMin(self, close_edge): # 获取最小权值的边
index = 0
min_weight = float("inf")
vertex = 0
while index < self.vertex_counter: # 不断循环根据close_edge中已有的边找到其中最小的一个,原理简单,实现简单
if close_edge[index][1] != 0 and close_edge[index][1] < min_weight:
min_weight = close_edge[index][1]
vertex = index
index = index + 1
return vertex
def LocateVertex(self, vertex): #定位定点在邻接表中位置的方法
index = 0
while self.vertex_set[index].data != vertex and index < len(self.adjacency_matrix):
index += 1 # 就是一个循环查找,遇到一样的事后就终止自加
return index
def GetEdges(self, edges): # 对图中的边进行升序排列和存储
horizontal = 0
while horizontal < self.vertex_counter: # 一层循环(行循环)
vertical = horizontal # 这一步主要是为了考虑到,对于邻接矩阵,其上三角部分和下三角部分完全对称,没有全部遍历的必要(当然,遍历了也不是不行)
while vertical < self.vertex_counter: # 二层循环(列循环)
if self.adjacency_matrix[horizontal][vertical] > 0 and self.adjacency_matrix[horizontal][vertical] < float("inf"):
index = 0
flag = True
while index < len(edges) and flag:
if edges[index][2] > self.adjacency_matrix[horizontal][vertical]:
edges.insert(index, [self.vertex_set[horizontal].data, self.vertex_set[vertical].data, self.adjacency_matrix[horizontal][vertical]]) # 根据行列标以及节点位置写入一个边
flag = False
index += 1
if flag:
edges.append([self.vertex_set[horizontal].data, self.vertex_set[vertical].data, self.adjacency_matrix[horizontal][vertical]]) # 同上
vertical += 1
horizontal += 1
def Kruskal(self, edges):
flag = [[] for i in range(self.vertex_counter)]
index = 0
while index < self.vertex_counter: # 初始化节点标记,用于判断节点是否属于同一连通分量
flag[index] = index
index += 1
index = 0
while index < len(edges): # 遍历每一条边直至所有边均属于同一连通分量
vertex_1 = self.LocateVertex(edges[index][0]) # 初始节点
vertex_2 = self.LocateVertex(edges[index][1]) # 终止节点
if flag[vertex_1] != flag[vertex_2]: # 能够成连接的节点
flag_1 = flag[vertex_1]
flag_2 = flag[vertex_2] # 提出节点
limit = 0
while limit < self.vertex_counter:
if flag[limit] == flag_2:
flag[limit] = flag_1 # 将符合条件的边并入同一个连通分量
limit += 1
index += 1
else:
edges.pop(index) # 将该边删除
print("Kruskal算法构造的最小生成树的边如下:")
for i in edges:
print(i)
if __name__ == "__main__":
graph = Graph()
graph.CreateGraph()
visited = graph.BFS()
flag = True
for i in range(len(visited)):
if visited[i] == "0":
flag = False
print("第%d个节点不可达" % i)
else:
continue
if flag:
print("所有节点可达")
graph.Prim(0)
edges = []
graph.GetEdges(edges)
graph.Kruskal(edges)
版权声明:本文为weixin_61864411原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。