匈牙利算法(Hungarian Algorithm)与KM算法(Kuhn-Munkres Algorithm)都用于求解任务分配问题。我学习这两个算法时阅读了一些文章,KM算法的细节没找到文章介绍得很清楚,这里就自己进行了总结。
目录
基本概念与匈牙利算法
KM算法中用到了匈牙利算法,可以先阅读下面这篇文章。
匈牙利算法
KM算法
算法过程
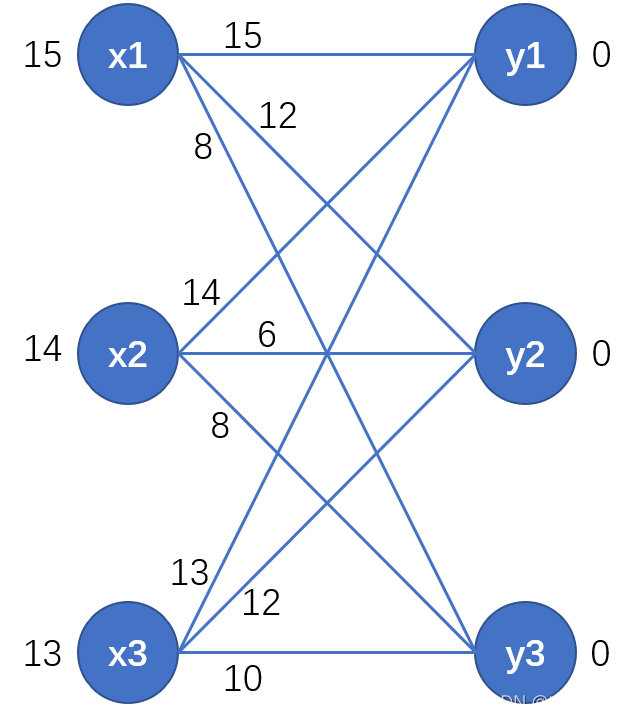
1、初始化顶标
为二分图中每个点赋值,称为这个点的
顶标
。顶标在求解过程中会变化。初始化顶标时,左侧的每个点的顶标都是
和它相连的权重最大边的权重
,像下面这个例子中,
x
1
x_{1}
x
1
、
x
2
x_{2}
x
2
、
x
3
x_{3}
x
3
的顶标分别是15、14、13。右侧的每个点的顶标都置为0。
2、寻找相等子图
在KM算法中,只有
一条边两端的点的顶标相加等于这条边的权重时,两端的点才能通过这条边进行匹配
,由这样的顶标相加等于权重的边组成的图称为原来二分图的
相等子图
。对左侧的任意点
i
i
i
,顶标用
A
[
i
]
A[i]
A
[
i
]
表示;对右侧的任意点
j
j
j
,顶标用
B
[
j
]
B[j]
B
[
j
]
表示。连接点
i
i
i
、
j
j
j
的边,权重用
w
[
i
]
[
j
]
w[i][j]
w
[
i
]
[
j
]
表示。对相等子图中的任意边和边两端的点
i
i
i
、
j
j
j
,都满足
A
[
i
]
+
B
[
j
]
=
w
[
i
]
[
j
]
A[i]+B[j]=w[i][j]
A
[
i
]
+
B
[
j
]
=
w
[
i
]
[
j
]
我们最终要找的匹配结果也是一个相等子图
。我们的例子目前的相等子图如下所示
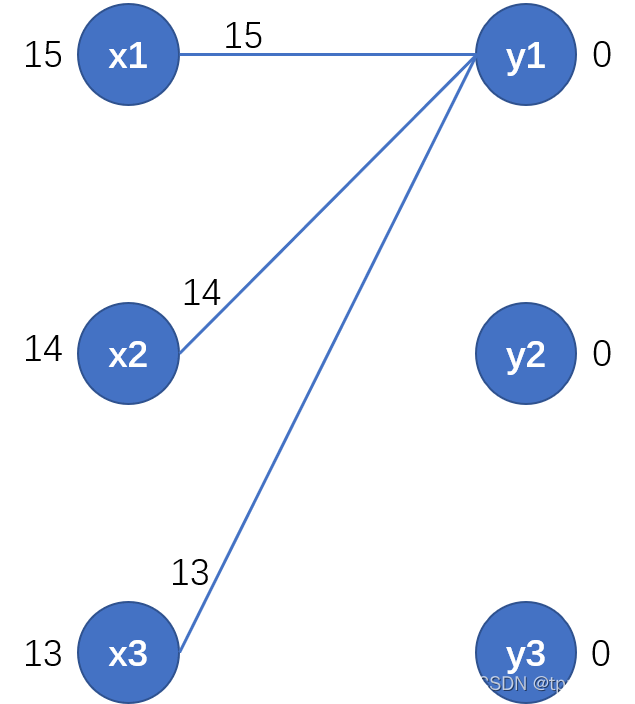
3、在相等子图中找完备匹配
需要
使用匈牙利算法在步骤2的相等子图中找到完备匹配
。注意子图包含原二分图中的所有点,如步骤2的例子中点
y
2
y2
y
2
、
y
3
y3
y
3
虽然没有被边连接,但也属于相等子图,因此该相等子图的完备匹配需要包含3对匹配。但是很显然这个图中我们最多只有1对匹配,说明这个相等子图不是我们要的最终结果,顶标需要修改。修改顶标就属于下一步了,这里我们先找完备匹配。
4、修改顶标
需要在步骤3的子图中找一条“
交替树
”,就是
不完整的增广路径
。交替树就是形如“未匹配边–匹配边–未匹配边–匹配边–未匹配边–…”的路径,未匹配边和匹配边交替出现。交替树和增广路径有相似之处,都是未匹配点作为起始点、未匹配边作为路径的第一条边,但是增广路径最后一条边必须是未匹配边、最后一个点必须是未匹配点,而交替树没有这两个必须。步骤3的例子中
x
2
−
y
1
−
x
1
x2-y1-x1
x
2
−
y
1
−
x
1
就是一条交替树。
我们之所以要修改顶标是因为步骤3没有找到完备匹配,也就是匈牙利算法里某一步找不到完整的增广路径,这一步得到的不完整的增广路径就是我们要的交替树。我们对
交替树中的所有点
进行修改顶标的操作。交替树中
左侧所有点的顶标都减去一个
d
e
l
t
a
delta
d
e
l
t
a
值,右侧所有点都增加一个
d
e
l
t
a
delta
d
e
l
t
a
值
。这个
d
e
l
t
a
delta
d
e
l
t
a
值是
使相等子图出现新的边,左侧顶标所能减去的最小值
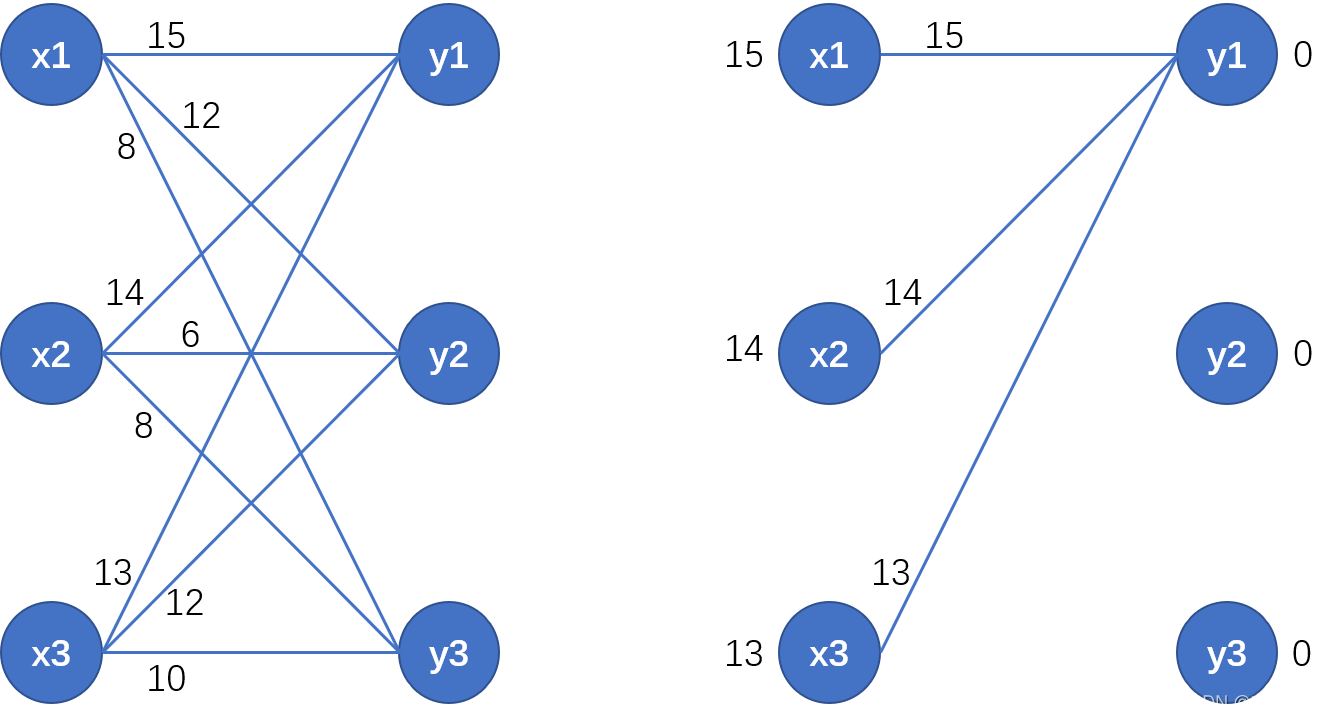
。如我们的例子如下面左图所示,目前的相等子图如下面右图所示,
x
1
x1
x
1
的顶标最少减去3变为12时,才能和右侧的点
y
2
y2
y
2
构成相等子图的新边,而
x
2
x2
x
2
最少要减去6。3和6取最小值为3,交替树
x
2
−
y
1
−
x
1
x2-y1-x1
x
2
−
y
1
−
x
1
左侧的点
x
1
x1
x
1
、
x
2
x2
x
2
都减3,右侧的点
y
1
y1
y
1
加3。
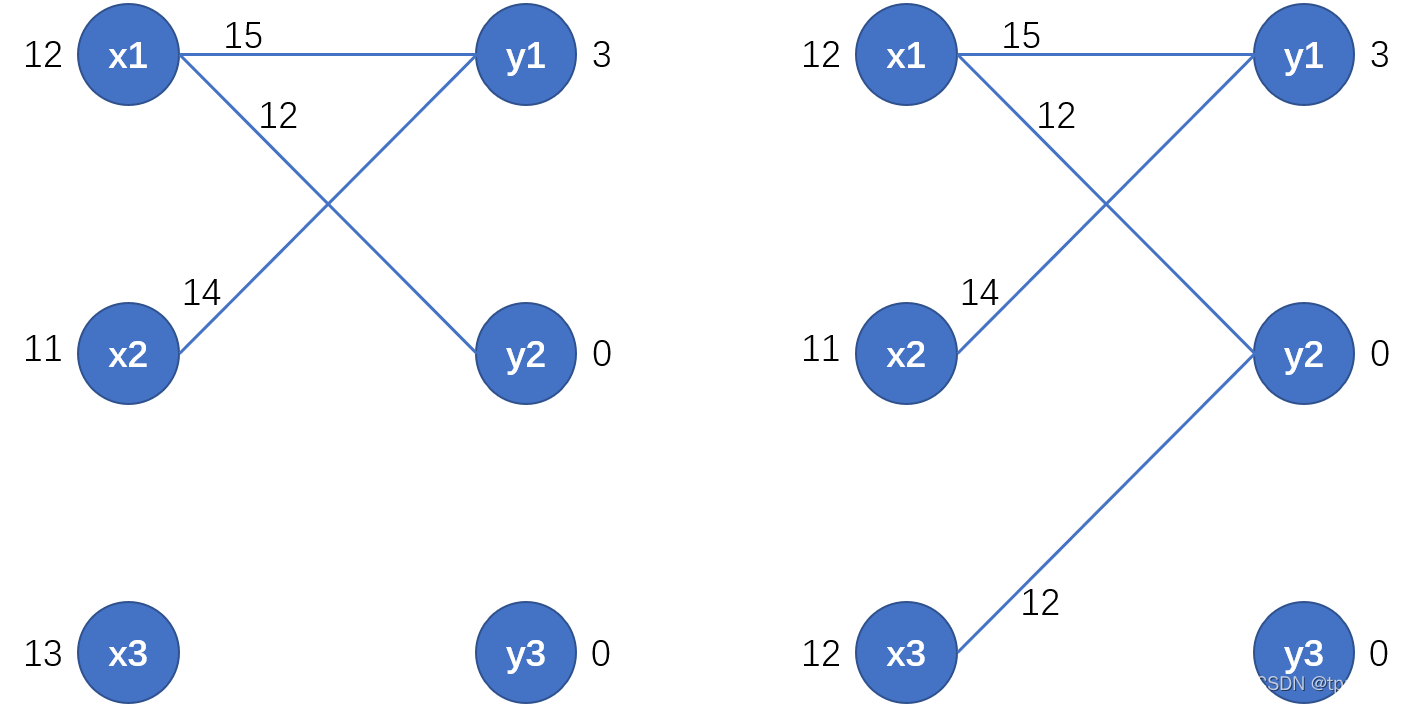
相等子图变为下面左图所示,增加了
x
1
−
y
2
x1-y2
x
1
−
y
2
这条边。但是由于
y
1
y1
y
1
顶标增加,
x
3
−
y
1
x3-y1
x
3
−
y
1
这条边没有了。KM算法每一步的相等子图中,
左侧每个点都要有和它相连的边
(除非出现下文补充部分的情况),
x
3
x3
x
3
就要修改顶标来和右侧点相连。
x
3
x3
x
3
最少减少1变为12时,可以和右侧点产生新的边
x
3
−
y
2
x3-y2
x
3
−
y
2
,于是新的相等子图就变为下面右图所示。接下来返回步骤3,直到在某个相等子图中找到完备匹配就停止算法。
5、
KM算法的完整过程到步骤4就介绍完了,但为了初学者更好理解,第5部分接着描述我们的例子的后续过程。
(1)在相等子图中为
x
1
x1
x
1
找到匹配边
x
1
−
y
1
x1-y1
x
1
−
y
1
。
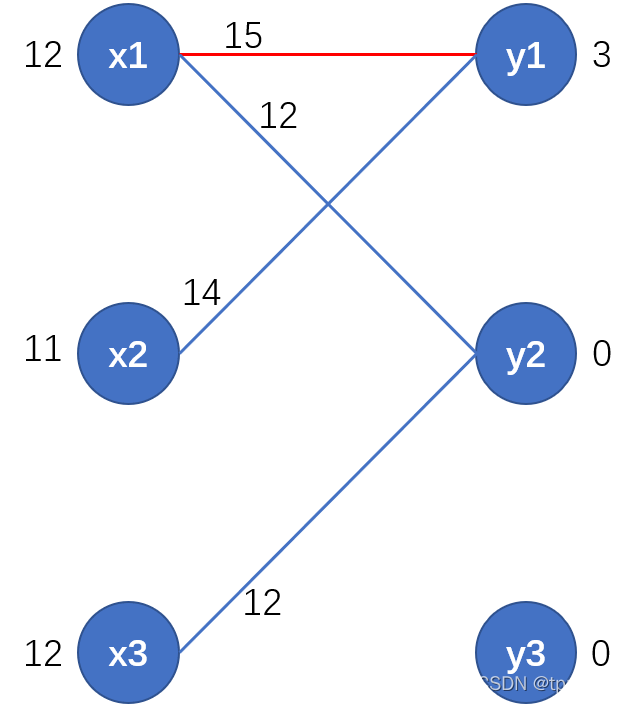
(2)为
x
2
x2
x
2
找匹配边时,找到增广路径
x
2
−
y
1
−
x
1
−
y
2
x2-y1-x1-y2
x
2
−
y
1
−
x
1
−
y
2
,进行匈牙利算法中的
匹配增广
操作,得到匹配边
x
1
−
y
2
x1-y2
x
1
−
y
2
、
x
2
−
y
1
x2-y1
x
2
−
y
1
。
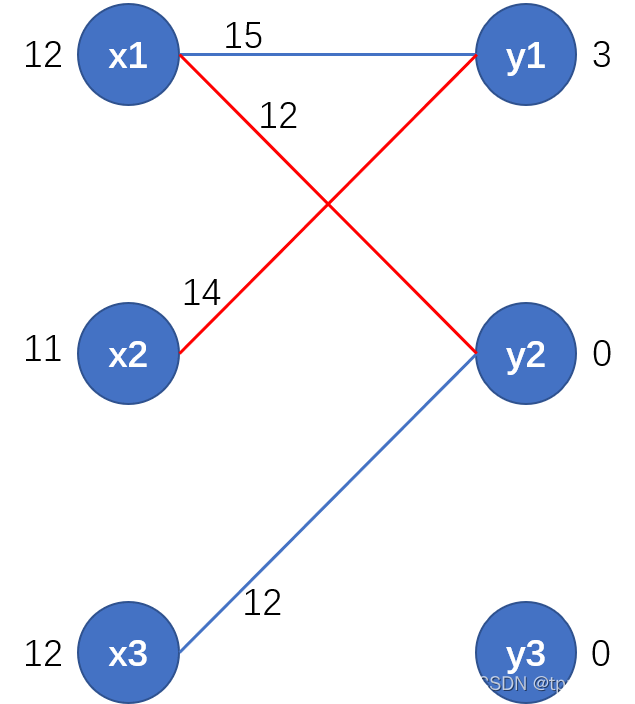
(3)为
x
3
x3
x
3
找匹配边时,没有增广路径,找到交替树
x
3
−
y
2
−
x
1
−
y
1
−
x
2
x3-y2-x1-y1-x2
x
3
−
y
2
−
x
1
−
y
1
−
x
2
。交替树左侧的点中,
x
1
x1
x
1
最少减4可以产生新边,
x
2
x2
x
2
最少减3,
x
3
x3
x
3
最少减2,4、3、2取最小值2,
x
1
x1
x
1
、
x
2
x2
x
2
、
x
3
x3
x
3
分别减2,
y
1
y1
y
1
、
y
2
y2
y
2
分别加2,产生新的相等子图。

(4)该相等子图可以得到完备匹配。最大权重和为36。

补充
KM算法求解要得到的是
权重之和最大的匹配,所以不一定是原二分图的完备匹配
。这里举一个例子进行补充说明。
(1)对下图中的例子初始化顶标,如下面左图。得到相等子图如下面右图。

(2)对(1)的相等子图进行匹配,如下面左图。找到交替树
x
3
−
y
1
−
x
1
x3-y1-x1
x
3
−
y
1
−
x
1
,修改顶标,得到新的相等子图,如下面右图。

(3)对(2)的相等子图进行匹配,如下面左图所示。找到交替树
x
4
−
y
3
−
x
2
x4-y3-x2
x
4
−
y
3
−
x
2
,修改顶标,
x
4
x4
x
4
的顶标减0.2时变为0,如下面右图所示。
左侧点的顶标变为0时,该点就被放弃匹配
。

(4)KM算法最终得到的匹配如下面左图所示,权重和为2.5,
x
4
x4
x
4
、
y
4
y4
y
4
没有被匹配。而原二分图的完备匹配如下面右图所示,权重和为2.0。

总结
KM算法步骤如下:
1、
初始化顶标
。左侧的每个点的顶标都是和它相连的权重最大边的权重,右侧每个点的顶标都是0。
2、
得到相等子图,用匈牙利算法在相等子图中找到完备匹配
。相等子图包含原二分图中的所有点。
3、
如果找不到,就找步骤2中的一条交替树,修改交替树中点的顶标
。交替树左侧所有点的顶标减
d
e
l
t
a
delta
d
e
l
t
a
,右侧点加
d
e
l
t
a
delta
d
e
l
t
a
,
d
e
l
t
a
delta
d
e
l
t
a
是使相等子图出现新的边,左侧顶标所能减去的最小值。
4、
重复步骤2、3,直到找到某个相等子图的完备匹配时停止
。如果过程中左侧某个点的顶标被减到0,该点就被放弃匹配。