源自:系统工程与电子技术
作者:张晔, 侯毅, 欧阳克威, 周石琳
摘 要
单变量序列数据分类涉及现实世界的诸多应用领域,具有重要的研究意义与应用价值。目前,单变量序列数据分类领域的发展处于深度学习逐渐取代传统方法的关键时期,但相关的归纳综述仍然很少。为了促进未来研究, 本文对单变量序列数据分类方法进行了全面的总结, 根据提取分类信息的不同, 将现有分类方法分为基于形状信息、基于频率信息、基于上下文信息以及基于信息融合4种类别。此外, 本文依托公开数据集对典型分类方法进行了对比与分析, 并对未来研究方向进行了展望。
关键词
单变量序列数据分类 ; 形状信息 ; 频率信息 ; 上下文信息 ; 信息融合 ; 深度学习
引言
在大数据时代的背景下, 现实世界的诸多应用领域产生了大量的序列数据, 例如, 图像轮廓数据、生物医疗数据、电气设备监控数据和人体动作识别数据等, 这些序列数据需要得到妥善分析和管理[1-3]。常见的序列数据分析和管理任务包括分类[4-6]、预测[7-8]以及异常检测[9-11]等。作为最基本的任务之一, 分类任务将类别标签分配给未标记的样本[12]。
单变量序列数据作为最简单的序列数据类型, 其分类问题也是其他序列数据分类问题的研究基础。此外, 现实生活产生了大量的单变量序列数据, 对有效的分类方法有着广泛而迫切的需求。近些年来, Dau等[13]收集了来自诸多现实应用领域的128个单变量序列数据分类数据集, 组成加州大学河滨分校(University of California River-side, UCR)序列数据归档, 并持续更新。作为目前最全面的分类数据库, UCR归档使得不同分类算法的整体对比和分析成为可能, 极大地促进了序列数据分类领域的发展。
不同现实应用领域所产生的单变量序列数据存在很大差别, 这些数据在分类时面临的困难也不尽相同。例如, 图像轮廓数据容易受到形状扭曲的影响, 电气设备监控数据包含大量噪声和重复模式, 动作识别数据的不同动作片段之间关联困难等。面向不同类型的数据, 现有方法通常借助变换表示等手段从不同角度提取分类信息, 针对性地克服不同分类任务所面临的困难。考虑到一种分类信息往往不够充分, 新近方法又融合了多种分类信息以提升分类精度和泛化性能。根据提取分类信息的不同, 本文将现有分类方法分为基于形状信息、基于频率信息、基于上下文信息以及基于信息融合4种类别, 进而展开综述。
目前, 单变量序列数据分类领域的发展处于传统方法逐渐被深度学习所取代的关键时期。然而, 目前仅有少数综述工作关注到单变量序列数据分类任务[4-6]。本文全面梳理了近十年的典型单变量序列数据分类方法, 与现有综述工作相比, 本文的主要贡献可以概括如下:
-
(1) 本文是同时覆盖传统和深度学习方法的单变量序列数据分类综述, 并囊括了单变量序列数据分类领域的最新进展;
-
(2) 根据不同方法在分类信息上的区别, 本文对现有的单变量序列数据分类方法进行了全面梳理和细致分类;
-
(3) 作为序列数据分类方法的有效补充, 序列数据增强也在本文中得到了较为系统的回顾;
-
(4) 本文对典型分类方法进行了全面的实验对比, 并根据实验结果做出了较为深刻的讨论与总结。
1 单变量序列数据分类方法
一个单变量序列数据样本xn=(x1n, x2n, …, xTn) (n∈{1, 2, …, N})是由T个观测值组成的有序集合, 这些观测值均为实数, 并通常以相等的采样频率获取。每一个单变量序列数据都与一个类别标签yn相关联, 若存在C个类别标签, 则yn∈{0, 1, 2, …, C-1}。给定一组未标记的单变量序列数据, 分类任务是将这些序列数据一一对应地映射为一组预定义的类标签。
由于本文仅对单变量序列数据分类方法开展综述, 因此在下文中将单变量序列数据简称为序列数据。此外, 单变量序列数据分类也被称为时间序列分类(time series classification, TSC), 这里的“时间”通常代指序列数据的横坐标, 包括但不仅限于时刻点(例如光谱频率、采样序号等)。根据引言中的讨论, 本节将现有分类方法分为基于形状信息、基于频率信息、基于上下文信息以及基于信息融合4种类别, 将在第1.1~1.4节分别展开介绍, 分类方法的分支框架如图 1所示。其中,DTW代表动态时间规整(dynamic time warping, DTW),KNN代表K近邻(K-nearest neighbor, KNN), DFT代表离散傅里叶变换(discrete Fourier transform, DFT),STFT代表短时傅里叶变换(short-time Fourier transform, STFT),DWT代表离散小波变换(discrete wavelet transform, DWT)。
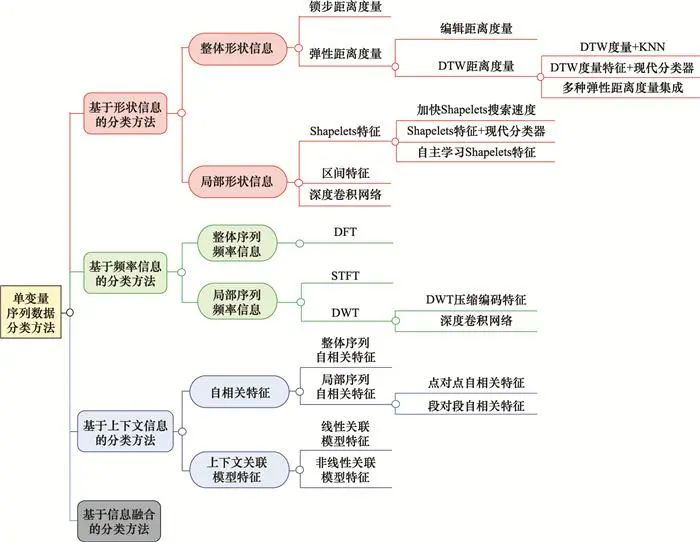
图1 单变量序列数据分类方法框架图
1.1
基于形状信息的TSC方法
序列数据是一组有序的观测值, 这些有序的观测值构成一条曲线, 从而直观地展示了序列数据的形状。不同类别的序列数据往往在形状上也有所区别, 因此诸多方法直接利用形状信息进行分类, 这类思路在TSC领域得到了最广泛的研究。根据分类方法作用范围的不同, 现有工作可以分为基于整体形状信息的分类方法和基于局部形状信息的分类方法两种类别, 下面分别展开综述。
1.1.1 基于整体形状信息的分类方法
序列数据的整体形状指有序幅值曲线的整体形状结构。由于不同类别的序列数据在整体形状结构上存在区别, 基于整体形状信息的分类方法通常通过计算待考察序列和模板序列之间的距离进行分类。根据采用距离度量的不同, 该类方法又可以分为基于锁步距离度量的分类方法和基于弹性距离度量的分类方法, 如图 2所示。
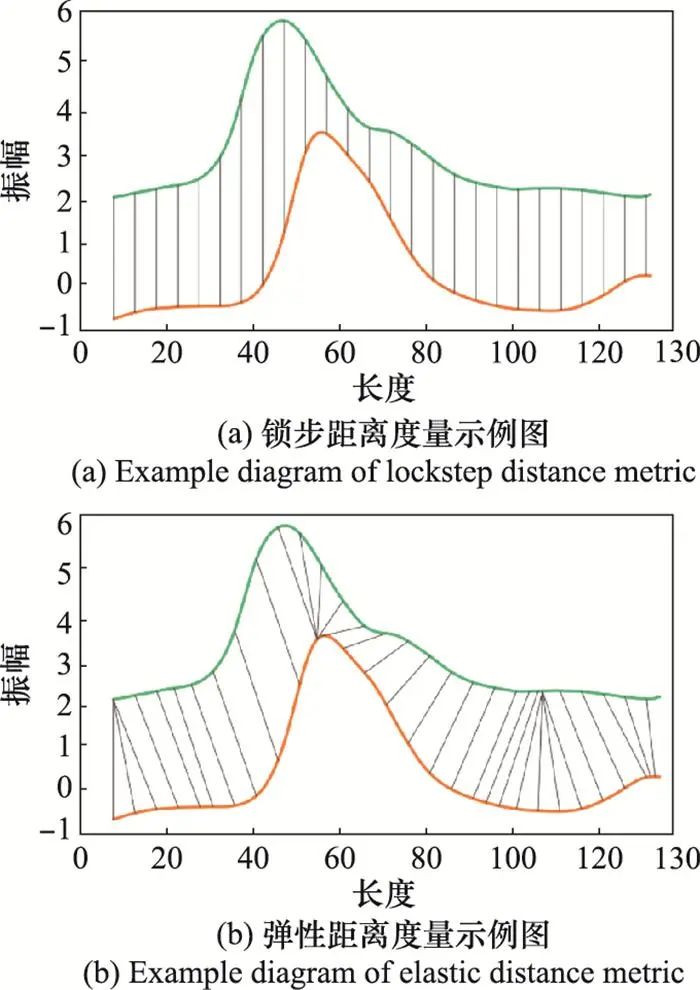
图2 锁步距离与弹性距离度量示例图
(1) 基于锁步距离度量的分类方法
锁步距离度量是最简单的序列数据距离度量方法。该方法首先对待考察序列与模板序列做向量减法运算得到差值向量, 然后计算该差值向量的Lp范数(通常采用L2范数[14]或L∞范数[15]), 从而得到两序列之间的距离。在计算距离的过程中, 由于两条序列需要在时刻点上一一对应, 因此这类方法又被称为“锁步”的距离度量, 如图 2(a)所示。“锁步”的特点虽然带来了计算速度的优势, 但对序列数据在时间维度上的扭曲、平移和幅度上的噪声、缩放非常敏感。
(2) 基于弹性距离度量的分类方法
为了适应序列数据在形状上的扭曲和缩放, 自20世纪90年代以来, 基于弹性距离的度量方法得到了广泛的研究。该类方法在计算距离时不再要求两序列在时刻点上一一对应, 而是可以弹性地适应序列数据的变化, 因此克服了基于锁步距离度量分类方法的缺陷。常用的弹性距离度量可以分为编辑距离度量和DTW距离度量两类。
1) 基于编辑距离度量的分类方法
该类方法将字符串匹配的思想引入TSC, 通过定义类似字符串匹配的操作进行相似性度量。主要的度量方法包括: 最长公共子序列(longest common subsequence, LCSS)距离度量[16-17]、基于实序列的编辑距离(edit distance on real sequences, EDR)[18]度量、基于实惩罚的编辑距离(edit distance with real penalty, ERP)度量[19]以及基于移动-分割-融合(move-split-merge, MSM)的编辑距离度量[20], 这些方法具有很强的渐进关系。
LCSS度量原本用于解决模式匹配中经典的LCSS问题, 在序列分类问题中, 该方法通过设置距离阈值θ判断待考察序列中的点是否与模板序列中的点相匹配, 被判定匹配的点无需在位置上一一对应, 从而“弹性”地搜索两条序列中的LCSS用于衡量两序列的相似度。LCSS度量量化了待考察序列与模板序列的共性, 但未将两者之间的差异计入度量。
EDR度量改进了LCSS的这一缺陷, 该方法参考了字符串匹配中编辑距离的思想, 在设定匹配条件后, 统计待考察序列通过替换、插入和删除3种操作完全匹配于模板序列所需的最少操作次数, 从而得到序列间的距离。EDR度量同时考虑了两序列之间的共性和差异, 但受到编辑距离的限制, 无法量化点与点之间的距离, 因此比较粗糙。
ERP度量对EDR度量进行了改进, 该方法不再统计转化操作次数, 而是直接计算点对之间的欧氏距离, 当点对不匹配时, 在待匹配点对应位置插入零值以示惩罚, 最终累加转换后的两序列所有对应点之间的距离得到序列间的距离。ERP度量更加细致地量化了序列之间的距离, 但零值惩罚的做法引入了较大的偏差。
MSM度量是目前最先进的编辑距离度量, 该方法针对点对不匹配的情况进一步细化了惩罚方式, 在待匹配点及其一近邻点中选取与模板点更近的点插入相应位置, 然后计算转换后的两序列之间的距离。事实上, 这种做法与下文所述的DTW度量已经非常接近。
2) 基于DTW距离度量的分类方法
编辑距离度量虽然允许匹配点在时间轴上进行动态调整, 但模板序列中的未匹配点只能与待考察序列中插入操作所生成的新点相匹配, 其本质依然是一对一的点匹配模式。DTW距离度量与编辑距离度量最大的不同在于, DTW距离度量允许一点对多点的匹配模式, 更加符合序列数据的特点。
DTW算法最早用于语音识别中单词的对齐和匹配。文献[21]最早将DTW引入TSC, 用于度量不同序列之间的距离。当前基于DTW距离度量的分类方法可以分为两类, 第一类方法关注对DTW度量本身的研究与改进, 并通常将DTW度量与简单的KNN分类器进行组合; 第二类方法关注如何借助DTW度量提取高维分类特征, 从而方便与更为先进的分类器结合。
① DTW度量+KNN
在很长时间内, DTW距离度量与KNN的组合所取得的分类效果很难被超越[22]。由于其出色的距离度量性能, 近些年来DTW距离度量已成为TSC领域的研究热点。然而, DTW度量存在对长时间序列效果不佳、计算复杂度较高等缺陷。针对这些缺陷, 现有方法提出了较多改进方案, 下面分别对其展开介绍。
长序列数据可能导致匹配点对在时间轴上发生严重偏移, 进而导致病态的匹配。当前工作主要通过设置约束窗口或设置约束权重两种思路解决这一问题, 典型工作包括加窗DTW(window constrained DTW, WCDTW)[23]和加权DTW(weighted DTW, WDTW)[24]。
WCDTW借助约束窗口限制DTW的匹配路径, 进而缓解上述问题。该方法分别尝试了一种线性约束窗口和一种非线性窗口, 并借助基于训练集的交叉验证(cross validation, CV)技术确定窗口所需参数。图 3展示了两种窗口的示意图, 其中C和Q分别代表两条待匹配的序列数据。实验结果表明, 在面向长序列数据时, WCDTW的分类效果明显优于DTW。

图3 DTW度量的两种约束窗示意图
WDTW认为WCDTW借助约束窗口截断匹配路径的做法拒绝了个例情况, 因此提出了一种更加平滑的匹配路径约束思路。
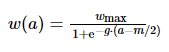
(1)
式中: a为时间距离;wmax为超参数,通常设为1;m为序列总长度;g为控制扭曲的惩罚等级。
该方法通过式(1)为时间距离较远的匹配点对设置小权值, 为时间距离较近的匹配设置大权值, 从而阻止匹配点对在时间上距离过远。WDTW是最先进的DTW改进方法之一。
较高的计算复杂度(O(n2))是DTW度量在大型TSC数据集上应用的主要障碍, 因此大量的研究工作致力于提升DTW的计算效率。目前, 降低DTW计算量的工作可以分为两类, 分别为设置下界距离和压缩匹配模板数量。典型的工作包括构造Keogh下界函数(lower bounding function of Keogh, LB-Keogh)距离[25]及构建DTW平均质心(DTW barycenter averaging, DBA)[26]。
构造下界距离的主要思想是, 下界距离不超过DTW距离, 且计算代价更小, 因此若待匹配序列与模板序列的下界距离大于阈值, 便可以跳过复杂的DTW距离计算。以基于LB-Keogh距离的分类方法为例, 该方法首先分段计算模板序列的上下界, 然后计算待匹配序列与模板序列上下边界的距离便得到下界距离。LB-Keogh距离的计算复杂度为O(n), 大大降低了原始DTW的计算复杂度。
压缩匹配模板数量的主要思想是, 分别找到每一类别的序列数据平均质心作为“原型序列”, 在测试时, 待匹配序列只需与这些“原型序列”进行比对, 从而大大降低算法的计算复杂度。以DBA为例, 该方法应用著名的动态质心平均技术[27]寻找每个类的质心, 这一技术将K均值聚类算法中的欧氏距离替换为DTW距离, 从而增强算法对形状动态扭曲的适应能力。此外, DBA也在类内求取多个质心以适应类内差异。
② DTW度量特征+现代分类器
长期以来, DTW度量与最简单的KNN分类器的组合一直很难被击败[22]。随着对DTW度量的改进逐渐遇到瓶颈, 一个自然的思路是, 利用DTW度量提取特征, 并使用更先进的分类器替换KNN分类器。利用DTW度量提取特征的常规做法是, 计算待考察序列与全体训练集序列数据的DTW距离, 并将这些距离作为待考察序列的特征。这种特征提取方法虽然反映了样本在整个系统中的模式信息, 但也存在提取特征速度慢、信息冗余等缺陷。围绕这些问题, 典型的改进工作包括基于高斯动态扭曲核支持向量机(potential support vector machine with Gaussian dynamic time warping kernel, GDTW-P-SVM)的分类方法[28]、基于增强SVM的DTW快速下界距离特征与SVM(DTW’s fast lower bound function feature classification using enhanced SVM, LBF-SVM)的分类方法[29]及基于AdaBoost原型选择(prototype selection with AdaBoost, PS-AdaBoost)的分类方法[30]。
GDTW-P-SVM最早尝试将DTW特征与更先进的分类器相结合, 该方法使用DTW度量替代高斯核SVM核函数中的欧氏距离度量, 然后训练多个二分类SVM分类器将多分类问题转化为多个二分类问题, 最后通过投票融合各SVM分类器的预测结果。GDTW-P-SVM虽然保留了DTW度量适应形状扭曲的优势和SVM的出色分类性能, 但该方法受限于DTW的计算复杂度而展现出高时间成本。
LBF-SVM降低了特征提取的计算复杂度, 该方法采用前文提到的LB_Keogh快速下界距离替代GDTW-P-SVM使用的DTW距离构建分类特征。这种做法虽然导致分类准确率略有下降, 但却极大地加速了训练和测试过程。
PS-AdaBoost引入了Adaboost分类器[31]进行分类, 该方法在DTW特征的每一维均建立带权值的弱分类器, 并通过训练优化每个分类器的权值, 从而实现对分类器和各特征维度的筛选。通过去除信息冗余, PS-AdaBoost的分类效果和计算速度得到了提升。
3) 集成多种弹性距离度量的分类方法
近些年来, TSC领域涌现出了数目众多的弹性距离度量方法, 这些方法各具优势, 适用于不同的分类场景。然而, 没有任何一种方法在分类精度和通用性两方面同时展现出明显优势[32]。因此, 一些工作考虑集成多种弹性距离度量从而提升分类性能和泛化能力。典型工作包括基于多种弹性距离度量集成(ensembles of elastic distance measures, EE)[33]的分类方法, 以及基于Proximity Forest的分类方法[34]。
EE借助KNN分类器对包括LCSS、MSM、DTW、WDTW等在内的11种常用的弹性距离度量开展了广泛的实验对比, 发现这些距离度量在分类精度上并没有显著差异, 且各自适用于不同的分类问题, 因此对这11种方法进行决策层的加权融合。虽然EE利用了诸多距离度量的互补性, 但也带来了极大的计算量。
Proximity Forest在分类树的每个节点构建R种分支策略, 每种分支策略包含从EE中随机选取的一种弹性距离度量以及从各类别中随机选取的序列数据原型, 然后寻找每个节点对应的最佳分支策略从而递归地生成分类树以及分类森林。Proximity Forest明显提升了EE的分类性能, 加快了EE的运算速度, 是目前性能最好的TSC方法之一。
1.1.2 基于局部形状信息的分类方法
序列数据的局部形状指有序幅值曲线的局部形状结构, 即曲线中“片段”的形状结构。现实生活产生的许多序列数据虽然在整体形状上非常类似, 但决定其类别归属的局部形状却大相径庭, 比如心电图的异常抖动、电气设备的故障监控数据等[13]。这些关键的局部信息在噪声的干扰下, 很难被以DTW度量为代表的基于整体形状信息的分类方法所捕捉。因此, 自2010年以来, 基于局部形状信息的分类方法逐渐成为TSC领域的研究热点。本文将其分为基于Shapelets的分类方法、基于区间特征的分类方法和基于卷积神经网络(convolutional neural network, CNN)的分类方法3个类别, 并分别展开介绍。
(1) 基于Shapelets的分类方法
Shapelets是序列中能够高度区分两种类别的子序列。基于Shapelets的序列分类方法利用一个或多个关键Shapelets与序列数据的距离(即Shapelet与等长子序列的最小距离)构建特征进行分类, 从而将距离度量的思想扩展到了局部序列[35]。使用叶片分类的例子简单说明Shapelets, 图 4给出了两种树木的叶片, 其整体形状极其类似, 主要区别在于叶颈与叶体的角度。将两种叶片的轮廓转换为序列数据表示后, 这种局部的差别很难被弹性度量等利用整体形状进行分类的方法所感知。而Shapelets却可以利用其捕捉局部模式和相位不变性的特点发现并可视化这种区别。
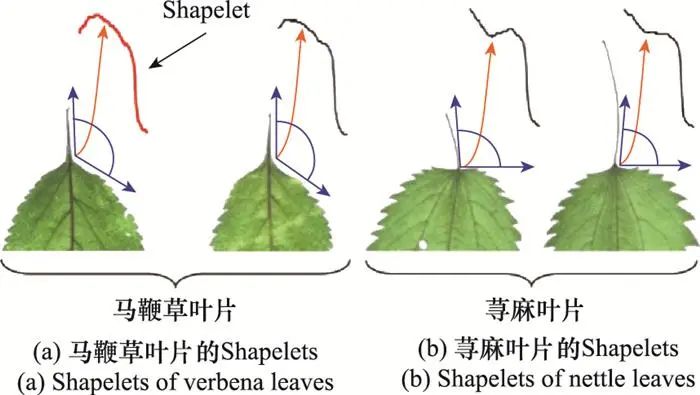
图4 Shapelets示例图
Shapelets最早由文献[36]提出, 该方法遍历训练集寻找所有满足预设长度要求的子序列作为候选Shapelets, 然后初始化一颗决策树, 在决策树的每个节点计算每条候选Shapelet与全部序列样本的最小距离, 并借助阈值dth将序列样本分为两类, 最后使用信息增益为每个节点寻找最佳的Shapelet和阈值dth组合, 从而完成分类决策树的构建。该方法的分类效果接近DTW-1NN, 但计算复杂度高达O(n2m4)(n为训练集中序列的数量, m为序列长度), 不具备实用性。
原始的Shapelets分类方法具备局部形状感知、平移不变性及解释性较强等优点, 但同时也存在计算复杂度高、分类特征与分类器难以解耦等缺陷。由于Shapelets分类方法的优势及存在的问题, 自提出以来迅速成为序列分类领域的研究热点。后续的研究主要集中在加快Shapelets的搜索速度、利用Shapelets提取特征及自主学习Shapelets 3个方向, 这3个方向存在明显的渐进关系, 下面依次展开综述。
1) 加快Shapelets的搜索速度
Shapelets的庞大候选集使该方法难以在现实应用中部署, 如何快速有效地搜索Shapelets成为急需解决的问题。主流方法引入符号聚合近似(symbolic aggregate approximation, SAX)[37]技术将序列数据转换为单词表示, 并从SAX单词表示中寻找Shapelets, 从而极大地加快了搜索速度, 这些工作包括快速Shapelets(fast Shapelets, FS)[38]及基于关键点的FS搜索(FS discovery with key points, FS-KP)[39]等方法。
FS利用SAX技术将原始序列转换为低维度、幅值离散的SAX单词表示, 然后分类别建立单词匹配表, 从而为每个类别寻找最具区分能力的k个SAX单词, 最后将这些SAX单词映射回原数据空间成为候补Shapelets, 进而构建决策树完成分类。该方法在保持分类精度的基础上可以将计算复杂度降至O(nm2)。
FS-KP使用关键点筛选技术进一步加快了FS的搜索速度, 该方法认为Shapelets中包含序列的一些关键点(如拐点、局部最小、最大点), 并使用这些关键点对子序列进行初步筛选, 然后再利用FS从筛选出的子序列中寻找候补Shapelets。FS-KP在保持分类精度的同时将FS的运算速度提高了4倍。
2) Shapelets特征+现代分类器
决策树虽然是成熟的分类器, 但其分类性能已经在许多领域被一些更加先进的分类器(如SVM、随机森林等)所超越。然而, 经典的Shapelets使用方式显然阻碍了这些先进分类器的部署。一个自然的思路是, 利用Shapelets与原始序列之间的距离构造分类特征, 并使用性能更好的分类器对这些特征进行分类。典型的工作包括基于Shapelets变换(Shapelet transform, ST)[40]特征的分类方法及基于FS选择ST(FS selection for ST, FSS-ST)的分类方法[41]。
ST最早使用Shapelets提取分类特征, 该方法首先借助假设检验技术[42]寻找区分性最强的k个Shapelets, 然后使用筛选出的Shapelets从每条序列数据中提取距离特征, 最后使用SVM等分类器对Shapelets特征进行分类。ST明显提升了原始Shapelets方法的分类效果, 并对后续基于Shapelets的分类方法带来启发。
FSS-ST提出了一种双层次的Shapelets快速筛选方法, 该方法首先从每个类别中提取多个原型序列, 然后借助关键点数量对原型序列进行筛选, 最终从筛选出的原型序列中提取Shapelets, 从而完成分类。与ST相比, FSS-ST明显提升了运算速度, 并略微提升了分类精度。
3) 自主学习Shapelets
自主学习Shapelets本质上仍然是一种Shapelets搜索技术, 与常规搜索技术不同的是, 其使用深度网络自动学习Shapelets, 而无需手工设计复杂的搜索流程。此外, 具有最佳判别能力的Shapelets可能不会出现在训练数据中, 自主学习Shapelets实现了对这种可能性的探索。基于上述原因, 自主学习Shapelets成为了TSC领域的研究热点之一。典型的工作包括学习时间序列的Shapelets (learning time-series Shapelets, LTS)[43]、三重Shapelets网络(triple Shapelet network, TSN)[44]及学习可解释的Shapelets (learning interpretable Shapelets, LIS)[45]。
LTS最早提出了自主学习Shapelets的思路, 该方法首先初始化R×K个Shapelets(R代表Shapelets的尺度数量, K代表每个尺度下候补Shapelets的数量), 然后使用初始化的Shapelets提取分类特征, 最后将这些特征输入单层感知机分类器, 通过反向传播实现对Shapelets的学习更新。值得一提的是, 该方法解决了提取Shapelets特征的不可微问题, 最终取得了优于ST的分类效果。
TSNs认为LTS学习到的Shapelets偏向样本数量更多的“大类”, 此外, 学习到的Shapelets不能很好地适应样本的个性差异。针对这些问题, 该方法在LTS的基础上额外增加了两个学习层次, 首先通过建立多个二分类逻辑回归分类器强制各类别的Shapelets数量相等, 维持类间均衡, 然后利用单层神经网络构建Shapelets生成器学习样本的个性差异, 最终构建和融合“整体特定”“类别特定”及“样本特定”3种层次的Shapelets特征进行分类。TSNs是目前最先进的Shapelets分类方法之一。
LIS认为学习到的Shapelets不再与数据集中真实的序列片段相似, 从而丧失了可解释性的优势。该方法因此引入生成对抗技术, 约束学习到的Shapelets更加接近真实子序列, 最终在保证分类准确性的同时, 增加了方法的可解释性。
(2) 基于区间特征的分类方法
基于区间特征的方法将原始序列数据分为若干个区间, 并从这些区间中提取手工特征, 进而完成分类。典型方法包括基于序列数据森林(time series forest, TSF)[46]的分类方法、基于序列数据特征袋(time series bag of features, TSBF)[47]的分类方法及基于SAX向量空间模型(SAX-vector space model, SAX-VSM)的分类方法[48]。
TSF提出了一种基于序列区间特征和随机森林分类器的分类方法, 在随机树的每个节点, TSF从每条序列数据中随机选取多种尺度的子序列, 将这些子序列的均值、标准差和斜率作为特征, 然后寻找每个子序列特征属性的最佳分离点并构建随机树, 最终融合全部随机树的决策进行分类。TSF降低了原始序列数据的特征维度, 提供了多尺度的特征表示, 然而该方法设计的子序列特征仍然比较粗糙。
TSBF拓展了TSF, 该方法首先从每条序列数据中随机选取一定数量的子序列, 提取子序列的区间特征用于构建子序列特征数据集, 然后建立两个随机森林分类器, 第一个分类器对子序列特征的分类过程建立基于类概率估计的密码本特征, 第二个分类器对密码本特征进行分类, 得到最终分类结果。TSBF的缺陷在于, 该方法构造的分类特征不具备平移不变性。
SAX-VSM提出了一种直方图特征表示方法克服上述难题, 该方法首先使用SAX技术将序列数据转换为单词表示, 然后统计各类别特有单词的频数, 得到各类别的直方图表示原型, 最后通过计算待考察序列单词表示与各类别原型单词表示之间的相似度完成分类。SAX-VSM构造的直方图表示具备良好的平移不变性, 此外与TSBF相比, 方法的分类速度得到了提升。
(3) 基于CNN的分类方法
近些年来, CNN在许多应用领域均取得了巨大的成功。在TSC领域, 基于CNN的分类方法已经成为研究热点之一。与Shapelets提取形状特征的方式相似, CNN使用滑动卷积核捕捉形状特征, 因此可以被归类为基于局部形状信息的分类方法。典型的基于CNN的工作包括多尺度CNN (multi-scale CNN, MCNN)[49]、面向TSC的深度神经网络基线[50]以及基于Inception网络的集成分类器InceptionTime[51]。
MCNN被认为是最早将CNN引入TSC领域的工作, 该方法通过尺度变换和频率变换等数据增强手段将单变量序列数据拓展为多变量序列数据, 然后借助多支路CNN分别从每个变量中提取分类特征, 从而完成分类。MCNN设计了一种有效的序列数据增强方法, 但该网络的结构存在冗余。
文献[50]提出了一种基于深度网络的TSC基线方法, 该方法包含多层感知器(multilayer perceptron, MLP)、全卷积网络(fully convolutional network, FCN)和残差网络(residual network, ResNet)在内的3种经典网络结构。其中, FCN是一个仅包含3个卷积层的全卷积结构的神经网络, ResNet借助残差连接将FCN加深至9层[52]。FCN和ResNet被广泛认为是基准的TSC网络, 这两种网络去除池化操作避免时间信息丢失, 使用全卷积结构减轻过拟合等网络结构设计思想为后续TSC网络提供了参考。
InceptionTime设计了一个6层ResNet, 每一层均引入Inception模块(一种包含多种尺度卷积核的并行结构网络模块)[53]用于增强网络的多尺度特征提取能力, 然后将网络重复训练5次, 并融合5个模型的分类决策, 从而缓解对浅层网络进行参数随机初始化时带来的不稳定性[54]。InceptionTime借助多尺度特征提取和决策融合提升了分类性能, 在基于CNN的分类方法中取得了更好的分类效果。
1.2
基于频率信息的TSC方法
频率是序列数据单位时间内完成周期性变化的次数, 序列数据的频率信息描述了整体或局部形状变化的快慢程度。复杂的序列数据被转换为不同振幅和频率的谐振荡(如正弦波)组合, 这种表示方式被称为频谱。频谱变换可以对整个序列数据进行, 例如DFT, 目的是分析整体序列的频率信息, 也可以对序列的局部区域进行, 例如STFT及DWT, 目的是分析局部序列的频率信息。频率信息揭示了序列数据隐藏在形状信息中的关键分类特征, 在TSC中起着极其重要的作用。
1.2.1 基于整体序列频率信息的分类方法
整体序列的频率信息描述了序列整体形状变化的快慢程度, 这些信息从频率构成的角度揭示了隐藏的分类特征, 是序列整体形状信息的有效补充。最为常见的频谱转换技术为DFT, 基于频率信息的分类方法往往将DFT的变换系数作为特征, 或从变换系数中进一步提取分类特征。然而, DFT损失了时间信息和局部信息, 近些年来不再是TSC领域的研究重点。
文献[55]提出了一种基于傅里叶近似符号(symbolic Fourier approximation, SFA)特征的分类方法, 该方法提取序列数据的前M个频谱系数, 并对每个频点的取值范围进行区间划分, 然后为每个区间设置字母代号从而建立多系数箱(multiple coefficient binning, MCB), 最后使用MCB映射表将序列数据转换为字符串特征, 如图 5所示, 从而借助前缀树分类器对这些字符串特征进行分类。SFA有效降低了噪声和相移的影响, 在基于整体频率信息的分类方法中取得了最佳的分类结果。
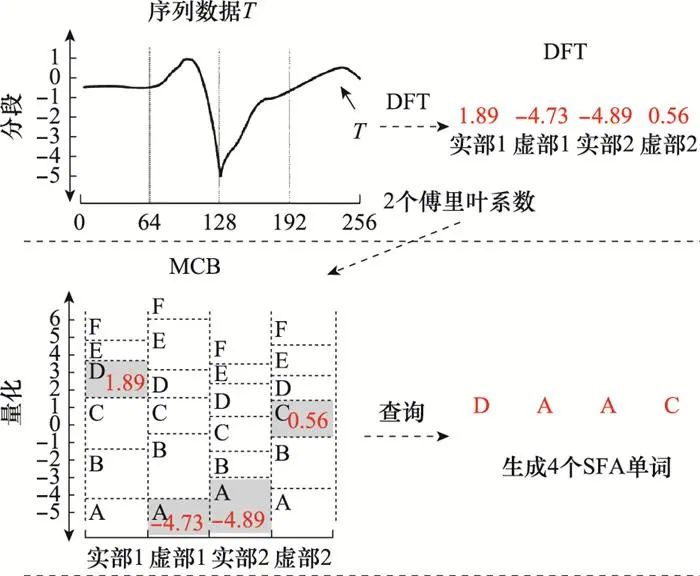
图5 DFT参数与字符串特征映射关系示例图
1.2.2 基于局部序列频率信息的分类方法
局部序列的频率信息描述局部序列形状变化的快慢程度, 这些局部的形状变化有时决定了序列数据的类别。例如, 心脏病病人的心电图异常往往出现在诸多周期中的一个, 强烈外界刺激使得人类脑电波在短时间内产生剧烈变化等。这些短促而关键的信号变化在噪声的掩盖下往往难以在整体序列的频率信息中展现, 却可以被局部序列的频谱所揭示。常用的局部序列频谱转换技术为STFT及DWT, 下面分别展开介绍。
(
1) 基于STFT特征的分类方法
STFT是由DFT拓展的一种数学变换, 用于计算非平稳序列数据的局部区域频率成分。在本节中, 非平稳序列数据指频率随时间变化的序列数据。现实生活产生的序列数据往往是非平稳的, DFT在处理非平稳信号时存在两个主要缺陷: 首先, DFT只能获取序列数据的总体频率成分, 但对各成分出现的时刻并无所知; 第二, DFT不善捕捉序列数据局部区域的频率信息。为克服这两个缺陷, STFT假定序列数据在固定窗函数的时间范围内是近似平稳的, 因此计算各滑动窗口的功率谱(power spectrum, PS), 从而保留了时间信息和局部信息。STFT在TSC领域得到了广泛的探索和应用, 典型方法包括基于SFA字符袋(bag of SFA symbol, BOSS)的分类方法[56]、基于向量空间BOSS(BOSS in vector space, BOSS-VS)的分类方法[57]及基于TSC字符特征(word extraction for TSC, WEASEL)的分类方法[58]。
BOSS使用STFT替换了SFA采用的DFT, 该方法计算序列数据的STFT系数, 通过MCB映射表将STFT系数映射为字符串表示, 进而统计字符串频数得到序列数据的字符串直方图表示, 如图 6所示, 然后构建直方图表示距离度量并使用KNN分类器进行分类, 最后融合多种尺度的STFT的分类结果完成分类。BOSS的分类效果明显优于SFA, 但也存在计算复杂度较高的缺陷。

图6 字符串直方图示意图
BOSS-VS降低了BOSS的计算复杂度, 在BOSS的基础上, 该方法引入文档频率技术[59]从每个类别中筛选出最具辨别力的字符串, 然后将这些字符串转换为直方图表示作为类别原型, 最后计算待考察序列与各类别原型之间的相似度完成分类。与BOSS相比, BOSS-VS的分类精度略有下降, 但明显提升了分类速度。
WEASEL从特征筛选的角度对前述工作做出改进, 该方法首先筛选具备辨别力的STFT系数, 并将这些系数映射为字符串, 然后统计字符串及相邻字符串组合的频数从而将序列数据转换为直方图特征, 最后连接多种尺度的直方图特征, 在去除特征冗余后, 使用SVM分类器进行分类。在基于STFT特征的分类方法中, WEASEL取得了最好的分类效果。
(2) 基于DWT特征的分类方法
由于STFT采用固定尺寸滑动窗, 该技术不能兼顾复杂非平稳序列数据对频率与时间分辨率的需求。DWT因此被引入TSC领域, 继承和发展了STFT局部化的思想, 同时又改进了固定尺寸滑动窗不能灵活适应序列局部变化的缺陷。通过对尺度函数和小波函数的伸缩平移, DWT可以根据时频分析要求聚焦到序列数据的任意细节, 是进行序列数据时频分析和处理的理想工具。基于DWT的TSC方法可以分为两种思路, 分别是构造DWT系数距离度量以及从DWT系数中提取特征, 下面分别对这两种思路展开介绍。
1) 基于DWT系数构造距离度量的分类方法
考虑到DWT出色的去噪性能, 使用平滑的低频DWT系数代替原始序列数据构造距离度量是一种简单而直接的思路。典型的工作是基于DWT特征度量(DWT feature measure, DWT-FM)[60]的分类方法。
DWT-FM对使用DWT系数构造距离度量的思路进行了详尽的探索和分析, 该方法使用Haar、Daubechies-20、Symlets-20和Coiflets-5等7种经典的小波对序列数据进行单次分解, 然后分别将每一种小波的低频变换参数与FastDTW分类器[61]相结合进行分类。该方法在UCR数据集上开展的实验验证结果表明, 大多数DWT低频参数的分类效果优于原始数据, 但不同小波基的变换参数在不同数据集上的分类效果存在很大差异, 最终建议为特定的TSC问题设计特定的小波。
2) 基于DWT系数提取特征的分类方法
① 基于DWT压缩编码技术的特征提取和分类方法
由于DWT在数据压缩领域取得的巨大成功[62], 一些工作将DWT压缩编码技术引入TSC领域, 通过对DWT系数进行压缩编码, 大大降低了分类特征的维度, 去除了冗余信息。
文献[63]分3个层次对DWT系数进行了压缩, 该方法首先通过香浓熵对Haar小波的多尺度变换系数进行初筛, 然后使用压缩编码技术对初筛的DWT变换系数进行降维得到分类特征, 最后设置阈值, 抛弃分类特征中被判定为噪声的部分。该方法在股票价格序列数据集上进行了实验, 分类性能要优于DFT系数度量。
尽管基于Haar小波基所构造的特征取得了不错的分类效果, 但其不平滑的小波基带来的阶梯效应限制了特征提取效率。为克服这一缺陷, 文献[64]引入了压缩性能更加优越的Daubechies-12、Symlets 20等正交或双正交的小波基, 然后利用DWT压缩技术提取分类特征, 并使用决策树进行分类。该方法在湖泊历史水位、股票收盘价格等分类数据集上对比了不同的小波基。实验结果表明, 大多数小波基的分类性能优于Haar小波。
② 基于DWT与CNN的分类方法
虽然神经网络可以自动获取分类知识, 避免复杂的手工特征设计, 但以CNN为代表的神经网络很容易受到噪声的干扰[65]。因此, 将DWT与CNN相结合的思路在近些年得到了探索, 并成为TSC领域的研究热点之一。典型的工作包括基于小波的FCN(wavelet based FCN, Wavelet-FCN)[66]和多级小波分解网络(multilevel wavelet decomposition network, mWDN)[67]。
WaveletFCN融合了多种分辨率的DWT系数深度特征, 该方法首先使用Haar小波对原始序列数据进行多分辨率分解, 然后使用多支路FCN分别从原始序列数据及不同分辨率的DWT系数中提取特征, 最后融合各支路的深度特征得到最终的分类结果。该方法在UCR数据集上开展了实验验证, 最终取得了优于FCN的分类结果。
mWDN将小波分解过程嵌入网络,如图 7所示, 从而自动学习适用于当前分类任务的小波基, 该方法使用Daubechies 4小波基初始化待学习小波基, 然后对输入数据进行3层DWT分解, 并连接每一层的高、低频参数输入对应的分类网络中进行分类, 最后对各分类器进行决策融合得到最终分类结果。mWDN借助CNN自动学习适用于当前任务的小波基, 为DWT与CNN的结合提供了一种新思路, 最终在40个UCR数据集上取得了略优于WaveletFCN的分类精度。
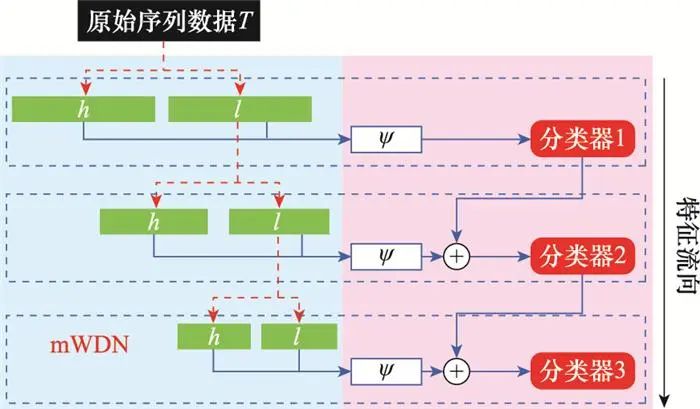
图7 mWDN框架示意图
1.3
基于上下文关联信息的TSC方法
在TSC领域, 上下文信息通常被理解为某些关键时间片段之间对于分类任务具有重要意义的相互关联信息。上下文信息不能从序列数据的单一时间片段中直接提取, 而是通过该片段与其他片段的关联关系中获得。例如, 在行为识别领域中, 不同动作的特定组合决定了行为类别; 在机器翻译领域中, 单词在不同的语境下具备不同的含义。根据上下文特征提取方式的不同, 基于上下文信息的分类方法可以分为基于自相关特征的分类方法和基于上下文关联模型特征的分类方法两类, 前者通过设置特定运算(例如, 向量乘法、距离度量)建立上下文之间的联系, 而后者通过构建复杂的线性或非线性模型自主学习上下文关系。
1.3.1 基于自相关特征的分类方法
基于自相关特征的分类方法通过设置特定运算构建序列数据中不同时间片段之间的关联关系, 并借助这种关联关系进行分类。根据关联作用范围的不同, 基于自相关特征的分类方法可以分为基于整体序列自相关特征的分类方法和基于局部序列自相关特征的分类方法两类, 前者通过自相关函数(auto correlation function, ACF)构建不同滞后时间下序列数据之间的相关关系, 因此是从序列的整体出发所建立的自相关关系; 后者构建不同滞后时间下序列数据的点或片段之间的相关关系, 是从局部出发所建立的相关关系, 下面分别对这两类方法展开介绍。
(1) 基于整体序列自相关特征的分类方法
基于整体序列自相关特征的分类方法通常使用序列数据的自相关系数作为特征进行分类, 自相关系数通过序列数据的ACF变换获取, 用于衡量序列数据在不同滞后时间下观测值之间的相关程度。在TSC领域中, 将自相关系数作为分类特征的思路在平稳序列数据或非平稳序列数据的分类问题中(本节中非平稳序列数据指均值和方差随时间变换的序列数据)均已得到了探索。
文献[68]最早尝试使用自相关系数对人工生成的平稳序列数据进行分类, 该方法借助多种自回归(auto regressive, AR)模型生成不同类别的序列数据, 然后计算这些序列数据的ACF、DFT变换系数以及AR模型参数, 得到原始序列的3种不同的变换表示, 最后使用欧氏距离、DTW等相似度度量分别对原始序列数据及其3种变换表示进行分类。实验结果表明, 自相关系数的分类效果仅次于AR模型系数。
由于现实世界产生的序列数据大多数是非平稳的, 文献[69]进一步探索了自相关系数区分平稳和非平稳序列数据的能力。该方法使用AR滑动平均(AR moving average, ARMA)模型生成大量平稳序列数据, 使用整合移动平均AR(AR integrated moving average, ARIMA)模型生成大量非平稳序列数据, 从而构建包含平稳及非平稳两类序列数据的分类数据集, 然后计算生成数据的ACF、偏ACF(partial ACF, PACF)和PS等变换系数, 最后借助距离度量对这些变换系数及原始序列数据进行分类。实验结果表明, 自相关系数区分平稳与非平稳序列数据的效果优于其他表示, 且分类精度随序列数据长度的增加而增加。
文献[70]将自相关系数作为分类特征引入包含大量现实世界数据的UCR数据集, 该方法首先使用ACF、PS及PCA对原始序列数据进行转换, 然后结合欧氏距离与1NN分类器分别对3种变换系数及原始序列进行分类。实验结果表明, ACF系数对应的分类结果优于另外两种变换表示, 但略差于原始序列数据。
(2) 基于局部序列自相关特征的分类方法
基于局部序列自相关特征的分类方法通过滑窗的方式, 以特定运算关联不同滞后时间下序列数据的点或片段, 从而将ACF构建的整体自相关关系推广到了局部。根据关联范围的不同, 这类方法又可以分为基于点对点自相关特征的分类方法和基于段对段自相关特征的分类方法, 下面分别对这两类方法展开介绍。
1) 基于点对点自相关特征的分类方法
基于点对点自相关特征的分类方法通过构建序列数据中不同时刻点之间的关联关系获取上下文信息。一种有效的构建任意两时刻点之间关系的思路是将序列编码为图像, 这种思路在最近一些工作中得到了探索。典型的转换图方法包括格兰姆角场(Gramian angular fields, GAF)[71-72]及马尔可夫转换场(Markov transition fields, MTF)[73]。GAF首先将序列数据转换为二维反余弦角度场, 然后分别通过余弦和正弦函数将角度场映射为格拉姆和角场(Gramian summation angular fields, GASF)与格拉姆差角场(Gramian difference angular fields, GADF); MTF统计序列中两点之间的转换概率, 从而将序列数据映射至概率场, 然后通过分位数箱对概率场进行转换。GAF反映了序列数据的幅度信息, 而MTF反映了序列数据的趋势变化信息, 两者存在很强的互补性。图 8依次给出了原始序列及其GASF、GADF及MTF转换图(在分类前转换图像通常会被调整为较小的尺寸)。
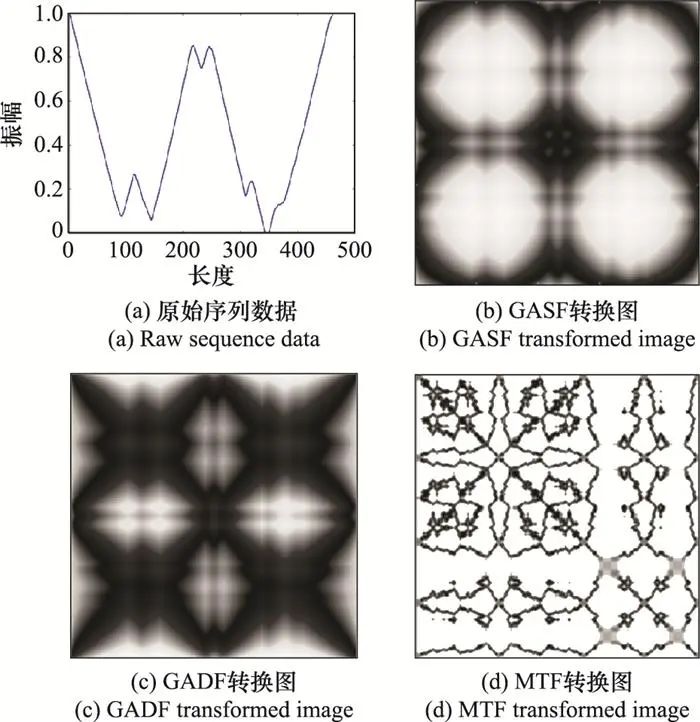
图8 原始序列数据及其GASF、GADF、MTF转换图
利用GASF及MTF的互补性, 文献将序列数据转换为双通道图像, 然后借助平铺CNN(tiled CNN, Tiled CNN)[74]从转换图中提取纹理特征进行分类。该方法在10个UCR数据集上取得了明显优于DTW+1NN的分类效果。
考虑到基于余弦函数构建时刻点关系的GASF图像损失了相位信息, 文献[72]进一步引入GADF, 将序列数据转换为三通道图像, 然后使用Tiled CNNs对转换图像进行分类。该方法在20个UCR数据集上开展了实验验证, 与文献[71]相比, 分类精度得到了提升。
虽然GAF及MTF从序列幅度及变换趋势两个角度生成转换图像的方式为后续工作带来启示, 但由于多通道图像导致的沉重计算量, 以及其较差的分类效果, 近些年来这两种转换图方法不再是TSC领域的研究热点。
2) 基于段对段自相关特征的分类方法
基于段对段自相关特征的分类方法通过构建序列数据中不同时间片段之间的关联关系获取上下文信息。这类方法同样将序列数据转换为图像, 其中最常用的转换方式是递归图(recurrence plot, RP), 一种分析复杂动态系统中序列数据周期性、混沌性和非平稳性的可视化工具[75]。该方法首先将序列数据映射到多维相空间中, 每个相空间状态对应着一个子序列, 然后计算相空间中每一个状态与其他状态之间的欧氏距离, 从而得到转换图中每个像素点的值。图 9给出了两条原始序列数据及其RP转换图。
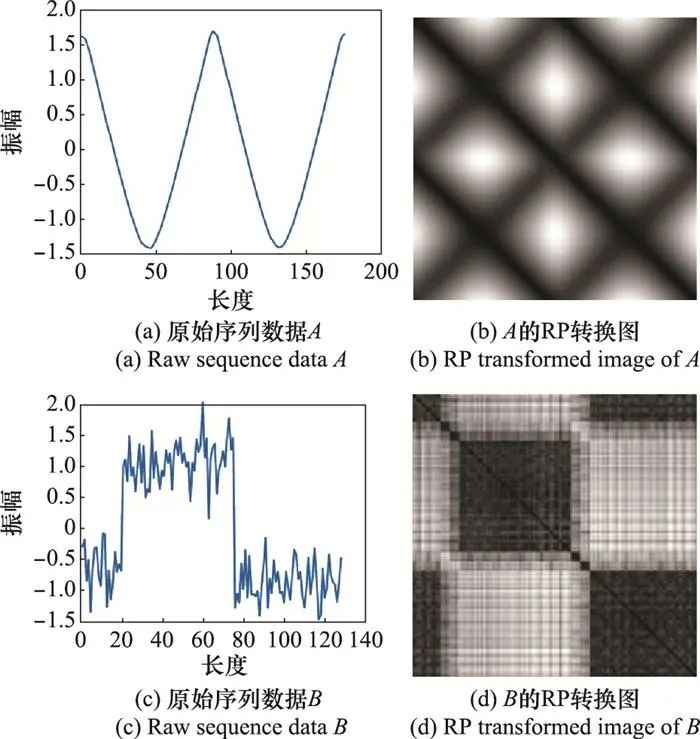
图9 原始序列数据及其RP转换图
目前提出的方法包括基于递归模式压缩距离(recurrence patterns compression distance, RPCD)的分类方法[76]、基于递归模式袋模型(bag of recurrence patterns model, BoR)的分类方法[77]、基于CNN的RP(RP classification using deep CNN, RP-CNN)的分类方法[78]以及基于Inception结构网络的多尺度符号RP(multi-scale signed RP classification using inception architectural networks, MS-RP-Inception)的分类方法[79]。
RPCD最早将RP引入TSC任务, 该方法将序列数据转换为RP图像, 然后使用Campa-Keogh距离[80]构建RP图像之间的距离度量, 最后使用1NN分类器进行分类。由于RP转换图具备更丰富的纹理信息, 该方法在38个UCR数据集的分类性能优于DTW+1NN分类器。
BoR引入了先进的图像特征提取技术, 该方法从每幅RP图中提取K个不同尺寸的图像块, 并使用SIFT技术从每个图像块中提取纹理特征, 然后将提取到的K个特征向量聚类为M簇, 并使用局部约束线性编码技术[81]将这M簇特征向量映射为直方图特征, 最后使用线性SVM对直方图特征进行分类。该方法在45个UCR数据集上取得了明显优于RPCD的分类效果。此外, 还可以引入图像分类领域更加先进的特征提取和分类技术进一步提升分类效果。
RP-CNN采纳了BoR的建议, 并使用CNN对RP转换图进行分类, 该方法构建了包含两层卷积层、两层全连接层及池化层的简单神经网络用于RP图像的分类, 并在20个UCR数据集上开展小规模的实验验证, 取得了优于BoR的分类效果。
MS-RP-Inception从两方面改进了RP-CNN。首先, 由于RP对序列数据尺度变化适应能力不足, 且存在严重的趋势混淆问题, 因此该方法提出了多尺度有符号RP(multi-scale signed RP, MS-RP)进行改进。其次, 由于CNN的多尺度特征提取能力较差, 该方法将Inception模块[53]引入FCN, 加强了网络提取多尺度特征的能力。MS-RP-Inception在85个UCR数据集上取得了基于RP转换图的方法中最佳的分类效果。
1.3.2 基于上下文关联模型特征的分类方法
基于上下文关联模型特征的分类方法通过复杂的线性模型(例如, AR模型、ARMA模型及ARIMA模型)或非线性模型(例如递归神经网络)自动学习上下文关系, 下面分别对这两类模型在TSC领域的相关研究工作展开介绍。
(1) 基于线性模型的上下文关联建模
使用线性模型进行上下文关联建模的方法, 面向平稳序列数据、噪声污染的平稳序列数据及非平稳序列数据3种不同类型的数据, 分别采用AR模型[68]、ARMA模型[82]及ARIMA模型[83]进行建模, 然后求取这些线性模型的参数作为TSC特征。文献[84]给出了计算模型系数的经典步骤如下。
-
步骤1 计算序列数据对应的ACF参数r;
-
步骤2 使用Durbin-Levinson递归估计ACF参数r对应的PACF参数λ;
-
步骤3 利用Akaike信息准则、Bayesian信息准则和Rissanen最小描述长度准则确定合适的模型阶数;
-
步骤4 使用Yule-Walker方程、ACF参数r、PACF参数λ及模型阶数估计模型参数。
前文已经提到, 将AR模型参数作为分类特征能够有效区分不同类别的平稳序列数据, 分类效果优于ACF、PS等变换特征及原始序列数据。
现实世界产生的平稳序列数据往往受到噪声的污染, 例如, 桥梁结构振荡响应信号反映了桥梁的健康程度, 但外部环境中的振动干扰了对桥梁的监测。文献[85]使用ARMA模型对这类数据进行建模, 该方法计算序列数据对应的ARMA模型参数, 然后借助χ2检验技术评估待考察数据对应的模型参数与每一条训练数据对应的模型参数之间的相似度进行分类。实验结果表明, 该方法能够有效区分处于健康状态和各种非健康状态的桥梁结构振荡响应信号。
文献[82]在包含大量现实世界数据的UCR数据集上验证了ARMA模型的分类性能。该方法首先计算序列数据的ACF系数、PACF系数及ARMA模型参数3种不同的变换表示, 然后构建集成分类器分别对上述3种变换表示及原始序列数据进行分类。实验结果表明, ARMA模型参数在4种表示中取得了最差的分类结果, 作者认为这是由于ARMA模型不适合对非平稳序列数据进行建模所导致。
为了应对非平稳信号的建模问题, ARIMA模型应运而生, 该模型可以通过多次差分操作将非平稳序列数据近似转换为平稳信号。文献[83]使用ARIMA模型对序列数据进行建模, 该方法首先计算序列数据的逆ARIMA模型参数, 并寻找训练集中各类别的中心, 然后计算待考察样本与各类别中心之间的欧氏距离, 最后用1NN分类器进行分类。该方法在工业生产指数和窦性心律心电图两个小型数据集上取得了成功, 由于现实生活产生的序列数据大多是非平稳的, 对于TSC任务, ARIMA模型展现出了线性模型中最好的泛化能力。
(2) 基于非线性模型的上下文关联建模
相对于线性模型, 非线性模型具备更好的泛化性能, 使用这类模型构建上下文关联关系时无需考虑序列数据的类型(如平稳信号或非平稳信号)。基于非线性模型的典型工作包括基于学习模式相似度(learned pattern similarity, LPS)的方法[86]、经典循环神经网络(recurrent neural network, RNN)[87]、长短时记忆(long short-term memory, LSTM)网络[88]及时间扭曲不变的回声状态网络(time warping invariant echo state network, TWIESN)[89]。
LPS借助回归森林建模序列片段之间的关联关系, 该方法使用滑动窗口将全部序列数据分为子片段, 按列连接这些子片段, 然后训练随机回归森林构建片段之间的关联, 最后统计每条序列数据落入随机森林的各叶子结点的元素数量作为新的表示, 并基于欧氏距离度量和1NN分类器进行分类。LPS使用回归森林构建适用于全体序列样本的局部非线性关系, 但这种方法构建的非线性关系仍然比较粗糙, 因此分类性能不佳。
近些年来, RNN因其构建上下文关联关系的优势而被引入TSC, RNN通过单个神经元之间的递归连接提取序列数据时间关联特征[90], 序列数据按时间顺序输入网络, 网络递归运作, 最终输出类别标签。经典的RNN因递归模式导致的梯度消失问题而不适用于长序列数据的分类。
LSTM(见图 10)对经典的RNN进行了改进, 该网络通过引入遗忘门、输入门和输出门3种门结构缓解了经典RNN的梯度消失问题, 从而更好地对长序列数据进行建模。

图10 RNN及LSTM结构示意图
TWIESN提出了回声状态网络(echo state network, ESN)[91], 该网络的核心是一个稀疏连接的随机RNN, 称为库空间, 序列数据的每个时刻点均可在库空间中映射至更高维度, 然后训练一个脊分类器判定序列数据在每一时刻点的类别, 最终利用所有时刻点的类别预测分布得到序列数据的最终类别。TWSEIN保留了序列数据内部关联, 并能够在一定程度上适应序列数据的扭曲变形, 但该方法对长序列数据的分类效果不佳。
1.4
基于信息融合的TSC方法
对于大多数TSC任务, 即使选择最优的序列数据变换表示, 单一的变换表示仍然难以提供足够的分类信息[82]。由于不同的变换表示从不同角度反映了序列数据的特点, 融合多种变换表示的分类信息便成为最直接的分类效果提升手段。此外, 考虑到各种变换表示均具备明确的物理意义, 基于信息融合的分类方法通常具备较强的可解释性。典型工作包括基于多变换表示集成(transformation-based ensembles, TE)的分类方法[70]、基于多变换表示决策融合(collective of transformation-based ensembles, COTE)的分类方法[82]、基于转换集成分层投票集合(hierarchical vote collective of transformation-based ensembles, HIVE-COTE)的分类方法[92]以及基于异构和集成嵌入森林(time series combination of heterogeneous and integrated embedding forest, TS-CHIEF)的分类方法[93]。
TE将序列数据中蕴含的分类信息分为时间关联信息、形状信息及频率信息, 该方法引入ACF、PCA及PS, 3种不同的变换表示分别对应上述3种分类信息, 然后使用线性SVM、贝叶斯网络等分类器分别对3种变换表示进行分类, 最后融合3种变换表示的分类决策得到最终分类结果。虽然TE通过融合多种变换表示的分类信息而明显提升了分类效果, 但这3种变换表示并未在物理意义上与3种分类信息准确对应。
COTE引入了Shapelets特征、PS以及ACF 3种变换表示, 从而更好地呼应了TE中的3种分类信息,如图 11所示。该方法首先使用上述3种变换技术对序列数据进行转换, 然后构建3种变换表示-集成分类器(包含KNN、线性SVM等8种经典分类器)组件, 这3种组件与EE[33]分类器组件共同构成COTE集成分类器, 最后通过对COTE包含的35种变换表示-分类器对进行加权融合得到最终的分类结果。COTE在72个UCR数据集上取得了当时最先进的分类效果, 但该方法也存在成员分类器的异构性差、分类决策更偏向整体信息等缺陷。
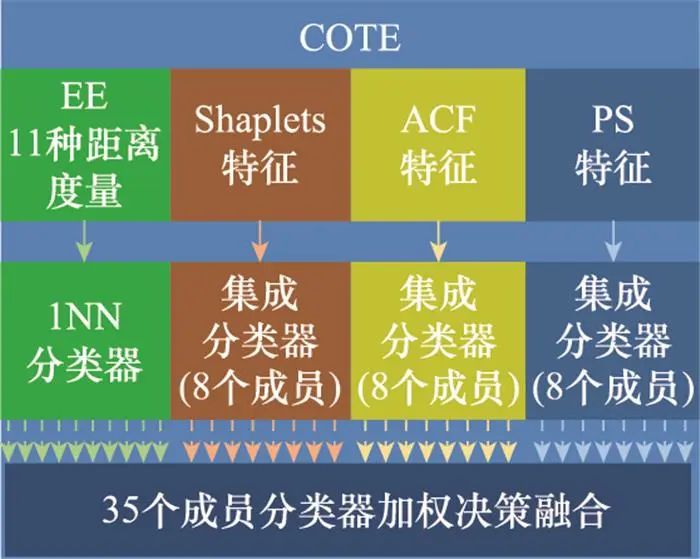
图11 COTE集成分类器组成结构图
HIVE-COTE通过引入异构分类器改善了COTE存在的缺陷, 该方法集成了5种异构组件, 如图 12所示, 分别是基于整体形状特征的EE集成分类器、基于局部形状特征的Shapelets集成分类器(包含8种异构分类器)、基于多尺度形状特征的TSF分类器、基于多尺度频率特征的BOSS[56]分类器以及基于多尺度自相关特征的随机间隔谱集成(random interval spectral ensemble, RICE)分类器。然后, HIVE-COTE分别对上述5种异构集成分类器组件以及各集成分类器内的异构成员分类器进行加权, 形成分层加权决策融合的分类框架进而完成分类。HIVE-COTE取得了优于COTE的分类效果, 但该方法的分类决策过于偏向形状信息, 且因复杂的结构导致极高的计算成本。
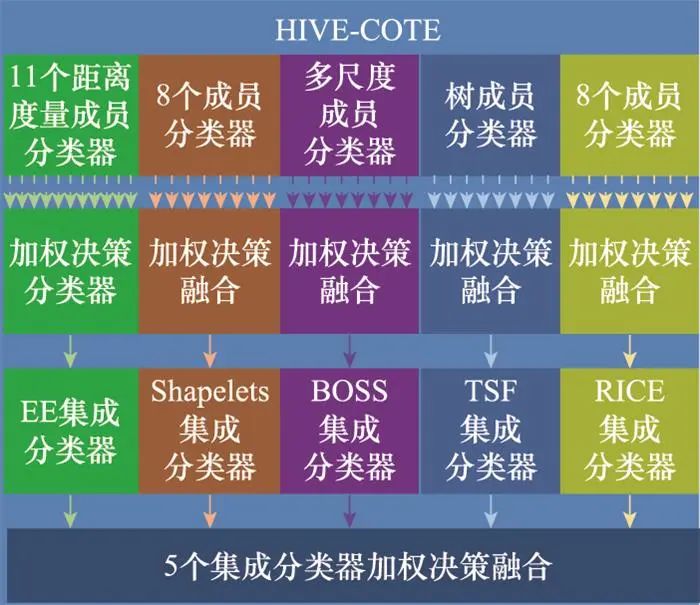
图12 HIVE-COTE集成分类器组成结构图
TS-CHIEF去除了TSF和Shapelets组件, 解决了HIVE-COTE偏向形状分类信息的问题, 并采用与Proxi-mity Forest[34]类似的融合方式以降低计算量。在分类树的每个节点, 该方法随机选取一个类别原型, 并借助EE、BOSS、RICE分别生成ce、cb和cr个分支策略, 然后寻找每个节点的最佳分支策略, 最后递归地生成分类树以及分类森林。实验结果表明, 与HIVE-COTE相比, TS-CHIEF在分类效果和计算速度两方面均得到了提升, 该方法是目前最佳的传统分类方法。
2 单变量序列数据增强方法
对于真实世界的诸多应用领域, 序列数据不仅难以获取(例如, 智能化运维产生的故障序列数据), 而且因专家知识的高昂成本导致标注困难(例如, 医学序列数据的标注)。数据的匮乏严重阻碍了TSC领域的发展。为了缓解这一问题, 数据增强人为地生成新的数据, 从而成为分类方法成功应用的关键因素[94]。因此, 在TSC方法之外, 本文也较为系统地回顾了不同的序列数据增强方法, 并将这些方法分为基于形状变换、基于频域变换、基于多样本混合和基于深度学习的4种类别, 分别展开介绍。
2.1
基于形状变换的序列数据增强方法
基于形状变换的序列数据增强方法直接对原始序列数据进行变换, 通过改变序列数据的形状生成新的样本。这类方法是最直接的序列数据增强方法, 典型工作包括窗口裁剪[95]、时间扭曲[95]、幅度缩放[96]以及增加噪声[96],如图 13所示。
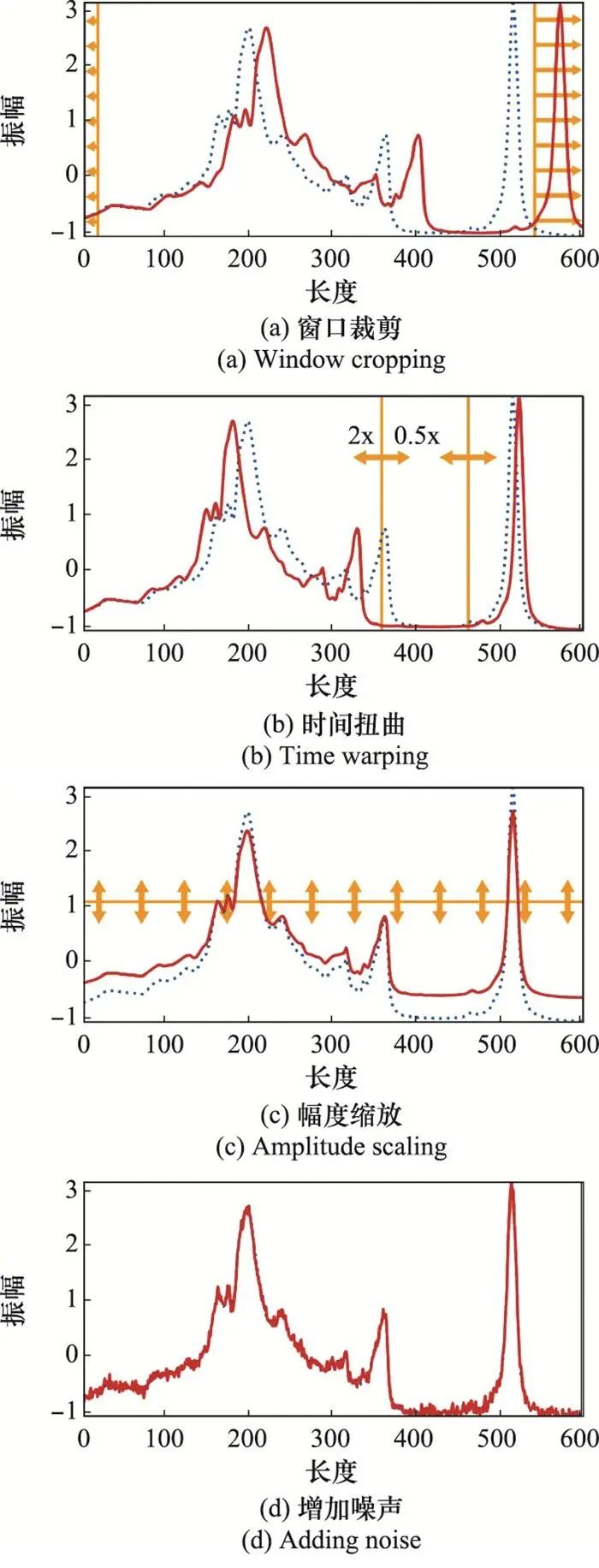
图13 基于形状变换的序列数据增强方法示例图
基于窗口裁剪的数据增强方法通过滑动窗口从原始序列数据中随机抽取多个子样本, 然后在测试阶段对每个切片进行分类, 最后借助多数投票机制得到最终的分类结果。对于该方法, 滑动窗口尺寸是重要的超参数。
基于时间扭曲的数据增强方法在原始序列中选择一个随机的时间范围, 并使用预定义的扭曲函数对其进行拉伸和收缩, 而保持其他时间范围不变。对于该方法, 扭曲函数的选择十分重要。
基于幅度缩放的数据增强方法通过随机标量值对序列数据的振幅进行缩放, 这些随机标量值可以通过不同的统计分布生成。
通过将少量噪声注入序列数据而不改变其标签, 是常用的数据增强方法。常见的噪声包括高斯噪声、尖峰等, 而噪声的均值、方差是重要的超参数。
基于形状变换的序列数据增强方法具备简单、直观的优势。然而, 这类方法对经验主义的超参数设置比较敏感, 方法在通用性方面也存在不足[96]。
2.2
基于频域变换的序列数据增强方法
基于频域变换的序列数据增强方法首先将原始序列数据映射至频域, 然后对频域特征进行变换从而得到新的样本。目前, 对于这类方法的相关研究仍然较少, 典型工作包括基于频谱振幅和相位扰动的数据增强(amplitude and phase perturbations based data augmentation, APP)方法[97]和基于STFT的数据增强(STFT based data augmentation, STFT-Augment)方法[98]。
APP首先对原始序列数据进行DFT, 然后随机地将振幅和相位谱特征中的一些片段替换为高斯噪声, 最后再进行频谱反变换得到新的样本。该方法帮助分类算法在异常检测数据集上取得了更好的分类效果。
STFT-Augment首先借助STFT对序列数据进行变换, 然后在频谱特征上应用局部平均和随机时序调整两种数据增强方法增加频谱多样性, 最后进行频谱反变换得到新的样本。与APP相比, STFT-Augment保留了一定的时间信息。
基于频域变换的序列数据增强方法通常更加适用于周期信号(例如, 心电图和声学信号)[99]。然而, 该方法在面对其他种类的信号时泛化能力不强, 可解释性较差。
2.3
基于多样本混合的序列数据增强方法
基于混合的序列数据增强方法通过混合多个相似的样本产生新的数据。不同方法主要在样本选取方法和融合方式上有所区别。典型工作包括少数类别过采样样本合成技术(synthetic minority over-sampling technique, SMOTE)[100]以及基于DTW曲重心平均的数据增强(DTW barycenter averaging data augmentation, DBA-Augment)[101]。
SMOTE是最经典的样本混合方法之一, 该方法首先在少量样本对应的类别中随机选择一个锚样本, 并在锚样本的KNN中随机选择一个邻居样本, 然后计算两个样本之间的向量差, 最后使用随机权重对向量差进行加权, 加权后的向量差与锚样本相加从而生成新样本。
DBA-Augment将序列数据的时间扭曲因素考虑进来, 从而改进了SMOTE。该方法在随机选择锚样本后, 使用DTW距离代替欧氏距离计算锚样本的KNN, 并进一步利用DTW距离为全部KNN样本进行加权, 最后使用DBA技术计算全部样本的质心, 从而得到新的样本。
基于多样本混合的序列数据增强方法通过混合多个相似的样本使得训练数据的分布更加丰富, 帮助分类算法取得了更好的效果。然而, 这类方法在面对具有多个“簇”的类别时表现不佳[99]。此外, 方法的解释性较差, 计算代价较高。
2.4
基于深度学习的序列数据增强方法
基于深度学习的序列数据增强方法通常采用生成式对抗网络(generative adversarial network, GAN)直接生成与训练样本接近的新样本。用于数据增强的GAN由生成器和判别器组成, 生成器以随机噪声作为输入, 输出生成扩充样本, 判别器则判断样本是否属于真实数据。典型工作包括循环条件GAN(recurrent conditional GAN, RCGAN)[102], 双向LSTM-CNN GAN(bidirectional LSTM-CNN based GAN, BiLSTM-CNN GAN)[103]以及时间序列GAN(time series GAN, TimeGAN)[104]。
由于RNN在构建时间关联方面的优势, RCGAN使用RNN作为生成器, 在每个时刻点均生成一段新的序列数据, 然后将这些序列数据送入判别器进行判别, 最后借助各时刻的决策投票产生最终的判别结果。此外, 该方法还引入条件输入生成特定类别的样本, 从而缓解了类别不均衡问题。
BiLSTM-CNN GAN对RCGAN进行了改进, 该方法使用特征提取能力更强的CNN替换了基于投票机制的判别器, 并将双向LSTM生成器生成的新样本直接送入CNN中进行判别, 从而在不影响准确度的基础上加快了判别速度。
TimeGAN是一个适用于多种应用领域的序列数据生成框架。该框架借助有监督的损失函数指导模型学习每个时刻点的数据条件分布, 并引入嵌入网络降低对抗学习空间的维度, 最终在股票、能源等诸多序列分类数据集上辅助分类模型取得了更好的效果。
基于深度学习的序列数据增强方法具备泛化能力强、无需繁琐的手工设计等优势。然而, 这类方法的解释性不强, 计算量较大, 也很难保证生成样本对应标签的准确性, 因此仍需得到进一步的研究。
2.5
序列数据增强面临的困难
目前, 尽管序列数据增强方法得到了越来越多的关注, 但仍然面临一些困难。首先, 现有数据增强方法在泛化性能方面存在明显缺陷[99, 105], 不同应用任务往往需要设计特定的数据增强方法; 其次, 现有数据增强方法在解释性方面存在不足, 很难判断数据增强是否会导致数据标签发生改变[94]; 最后, 由于不同的数据增强方法可能适配于不同的应用场景或分类模型, 目前依然缺乏针对序列数据增强的统一评价标准[94, 106]。这些困难限制了数据增强成为分类过程中的默认环节。
在序列数据增强以外, 迁移学习也常用于缓解数据匮乏问题。然而, 不同应用领域产生的序列数据存在很大差异, 这为寻找合适的“迁移域”带来困难, 最终导致迁移学习的效果不佳[107-108]。因此, 本文不再对迁移学习的相关方法展开介绍。
3 实验结果与分析
为了系统地对比和分析数量庞大的TSC方法, 本节从前文所述的分类方法中选择性能出色或具备重要意义的方法, 通过对比其在公开数据集上的分类表现, 梳理单变量TSC领域的发展现状和未来趋势。由于当前的序列数据增强方法存在泛化能力差、缺乏统一的评价标准等缺陷, 数据增强未成为分类过程中的默认一环。因此, 本文没有开展相关实验对不同的序列数据增强方法进行对比。
第3.1节首先介绍了本文采用的分类数据集和评价指标; 第3.2~3.5节对基于形状信息、基于频率信息、基于上下文信息和基于信息融合4种分类方法分别进行了对比和分析; 第3.6节对典型的TSC方法进行了整体对比和分析; 为了分析现有方法在不同应用领域的表现, 第3.7节分别在不同类型的数据集上进一步对TSC方法进行了对比和分析。
3.1 数据集、评价指标和模型参数介绍
3.1.1 UCR序列数据归档
UCR序列数据归档[13]是研究与分析单变量TSC问题的专用数据库, 也是目前最全面的数据库。其包含了128个公开、已标注的单变量序列数据集, 每个数据集由预先划分的训练集和测试集组成。UCR归档中的序列数据从现实世界中的诸多应用领域采集而来, 典型的数据类型包括图像轮廓数据、设备监控数据、动作识别数据、生物医疗数据以及其他传感器数据等, 图 14中给出了部分数据示例。近年来, TSC社区的诸多学者为UCR归档贡献了大量数据集, 围绕UCR归档展开的研究也十分广泛。这些研究的主要目的是开发通用的或适用于特定数据类型的TSC方法。
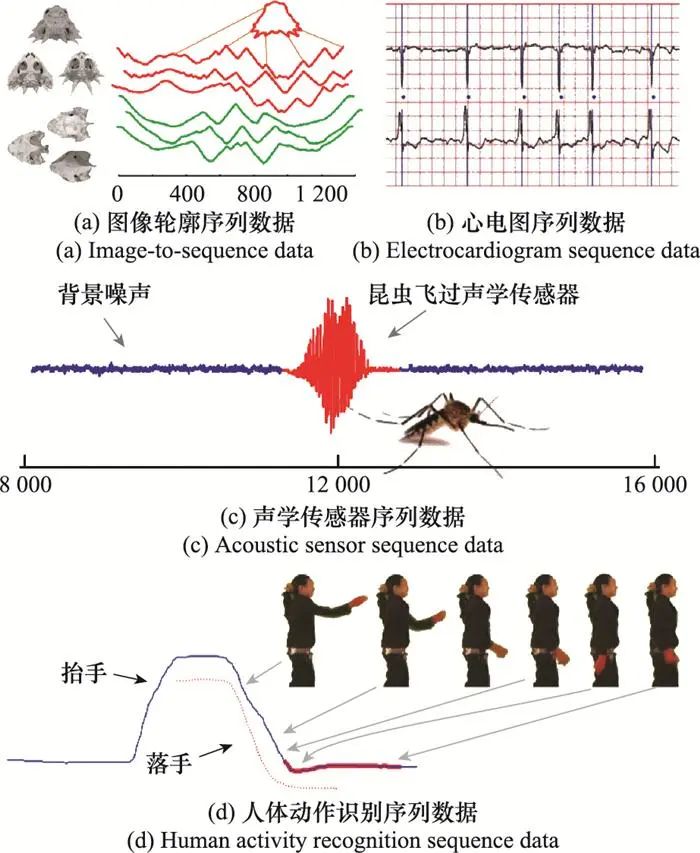
图14 几种常见的序列数据类型示例图
按照领域惯例, 本文从UCR归档中选择85个最常用的数据集[6]用于对比不同的分类方法。在下文中, 若无特殊说明, 参与对比的分类方法均在这85个数据集上进行评估。
3.1.2 评价指标和模型参数
在TSC领域中, 面向单一数据集的常用评价指标包括分类精度、F1分数和加权F1分数等[4]。面向多个数据集的常用评价指标包括平均分类精度、平均类错误率(mean per-class error, MPCE)和算术平均排名等[50]。其中, MPCE在平均错误率的基础上进一步考虑了各数据集的类别数量差异; 算术平均排名是当前算法在各数据集上精度的平均排名。本文采用UCR归档作为基准数据集, 因此使用平均分类精度和平均算术排名两种面向多数据集的评价指标对不同的分类模型进行评估和对比。
为了直观展示不同分类方法的整体分类表现, 按照TSC领域的通常做法, 首先采用弗里德曼检验拒绝原假设[109], 然后利用附带Holm校正的Wilcoxon符号秩检验衡量不同方法分类结果之间差异的显著性[110], 最后使用关键区别图[111]直观显示对比结果, 关键区别图可以同时展示算法的平均分类精度和平均算术排名两个指标, 如图 15所示。
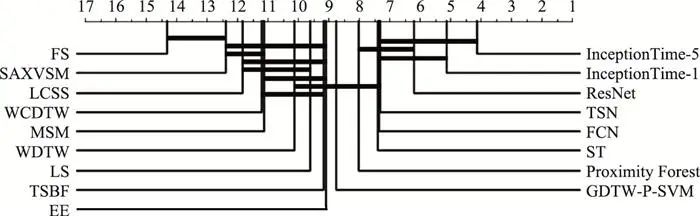
图15 基于形状信息的分类方法的关键区别图
在本节中参与对比的分类模型在不同UCR数据集上的分类精度从对应文献、UCR归档官方网站[13]获取, 或根据公开代码复现而来。对于复现的传统方法, 超参数将严格按照方法原文进行设置。对于复现的深度学习方法, 本文统一使用交叉熵损失函数和Adam优化器[112]对网络进行训练, 其余网络参数严格按照方法原文进行设置。
3.2
基于形状信息的分类方法对比与分析
本节对典型的基于形状信息的分类方法进行对比和分析, 选取的对比方法列举如下。
-
(1) 本节忽略了分类效果较差的基于锁步距离度量的方法;
-
(2) 在基于弹性距离的方法中, 本节选择LCSS、MSM、WCDTW、WDTW、GDTW-P-SVM、EE以及Proximity Fo-rest;
-
(3) 在基于Shapelets的方法中, 本节选择FS、ST、LTS以及TSN;
-
(4) 在基于区间特征的方法中, 本节选择SAX-VSM和TSBF;
-
(5) 在基于深度学习的方法中, 本节选择FCN、ResNet、InceptionTime-1(单一Inception网络)以及InceptionTime-5(多个Inception网络集成)。
整体分类效果如图 15所示, 图中最上方的刻度轴表示方法的分类效果排名, 加粗横线表示对于alpha=0.05的Wilcoxon符号秩检验, 同一条横线内的方法在整体分类精度上没有显著区别(后文同)。在基于形状信息的分类方法中, 基于局部形状信息的方法优于基于整体形状信息的方法; 基于特征提取的方法优于基于各种距离度量; 集成方法优于单一方法; 值得注意的是, 基于深度学习的分类方法展现出了最先进的分类性能。对于基于弹性距离度量的分类方法, 首先, DTW度量(WCDTW, WDTW)取得了对编辑距离度量(LCSS, MSM)的微弱优势, 这是由于在计算待匹配点对之间的距离时, DTW度量采用的欧氏距离相对于编辑距离更加精确, 而且一对多的点匹配模式相对于一对一的点匹配模式更具泛化性; 其次, 不同的距离度量展现出的互补性同样值得关注, 这种互补性是集成类方法(EE, Proximity Forest)的主要动机; 最后, 弹性距离度量特征与先进分类器的组合(GDTW-P-SVM)也取得了可观的分类效果。不同的距离度量在点匹配模式和动态路径规划上区别较大, 因此如何根据分类任务选择合适的度量模式, 以及如何更高效地提取“弹性”分类特征仍然值得探索。
对于基于Shapelets的分类方法, 早期的Shapelets方法(FS)已被基于Shapelets特征的方法(ST, LS, TSN)所超越。其中, 自主学习Shapelets(LS, TSN)借助神经网络强大的特征提取能力取得了出色的分类效果, 并成为最近的研究热点。在未来, 基于Shapelets的分类方法仍然需要考虑如何更高效地与深度学习相结合, 然而, 考虑到这类方法与CNN的相似性, 寻找新的增长点十分困难。
对于基于区间特征的分类方法, 基于重复模式直方图特征的方法(SAX-VSM)在分类效果上明显弱于基于手工区间特征的方法(TSBF), 这是由于, 受到噪声和个体差异的影响, 原始数据表示很难直接用于发掘重复模式特征。因此, 如何设计更有效的手工特征仍然值得探索。
对于基于深度学习的方法, 这类方法取得了在基于形状信息的方法中最先进的分类效果。考虑到当前仅有少数的经典网络结构(FCN, ResNet, Inception)得到了验证, 基于深度学习的方法仍具备较大的研究潜力。潜在的研究方向在于, 更广泛的经典网络结构应该得到验证, 以及如何借助传统方法的思想指导网络结构的设计。
3.3
基于频率信息的分类方法对比与分析
本节对基于频率信息的分类方法进行对比和分析, 选取的对比方法列举如下。
-
(1) 在基于整体序列频率信息的方法中, 本节选择SFA;
-
(2) 在基于STFT特征的方法中, 本节选择BOSS和WEASEL;
-
(3) 在基于DWT特征的方法中, 本节选择Wavelet-FCN和mWDN-FCN-RCF。
上述方法的对比实验在40个UCR数据集上开展, 与文献保持一致, 实验结果如图 16所示。

图16 基于频率信息的分类方法的关键区别图
从分类结果中可以发现, 首先, 基于整体序列频率信息的方法(SFA)取得了最差的分类效果; 其次, 与基于形状信息的SAX-VSM等方法相比, BOSS与WEASEL同样建立了基于重复模式的直方图特征, 却取得了更好的分类效果, 这说明频域表示更适合提取重复模式特征; 最后, DWT与CNN的结合(mWDN, WaveletFCN)取得了最先进的分类效果, 这验证了DWT表示的优越性, 以及DWT与CNN的互补性。考虑到不同应用领域所产生的序列数据具备个性化特征, 如何借助神经网络学习适合当前分类任务的小波基将是未来的研究方向之一。
3.4
基于上下文信息的分类方法对比与分析
本节对基于上下文信息的分类方法进行对比和分析, 选取的对比方法列举如下。
-
(1) 在基于序列自相关系数的分类方法中, 本节选择了基于ACF距离度量的分类方法;
-
(2) 在基于局部序列自相关特征的分类方法中, 本节忽略了效果较差的基于点对点自相关特征的方法, 选择RPCD、BoR、RP-CNN、MS-RP-FCN以及MS-RP-Inception等基于段对段自相关特征的方法;
-
(3) 在基于上下文关联模型特征的分类方法中, 本节忽略了效果较差的基于线性模型特征的方法, 选择LPS和TWIESN等基于非线性模型特征的分类方法。上述方法的对比实验在39个UCR数据集上开展, 与文献[76]保持一致, 实验结果如图 17所示。

图17 基于上下文信息的分类方法的关键区别图
从图 17的实验结果中可以发现, 首先, 基于整体序列自相关特征的分类方法弱于基于局部序列自相关特征的分类方法; 其次, 基于非线性模型特征的方法取得了较差的分类效果, 这是由于以RNN为代表的非线性模型难以对长序列数据进行建模; 最后, 基于段对段自相关特征的方法展现出了最好的分类效果, 在这类方法中, 相对于基于RP的手工特征, CNN从RP中提取的深度特征取得了更好的分类效果, 这是由于CNN所提取的纹理特征更为有效。考虑到转换图带来的庞大计算量, 如何通过网络结构的设计将转换图构建的上下文关系“网络化”, 形成“端对端”的网络结构, 仍然值得探索。
3.5
基于信息融合的分类方法性能对比与分析
在基于信息融合的分类方法中, 本节选择COTE、HIVE-COTE和TS-CHIEF, 忽略性能较差的HCF-TSC以及TE。
从图 18的分类结果中可以发现, 异构分类信息层面的融合方法(HIVE-COTE)优于分类器层面的融合方法(COTE), 这验证了形状信息、频率信息以及上下文信息对于TSC任务的互补性; 此外, 不同于上述两种方法, TS-CHIEF从特征层面融合分类信息, 以相对较小的计算代价取得了更好的分类效果, 展示了特征融合思路的研究潜力。未来的研究趋势是, 需要继续提升各组件分类器的性能, 并探索特征层面的融合技术, 从而更好地去除信息冗余, 降低计算量。

图18 基于信息融合的分类方法的关键区别图
3.6
TSC方法的整体对比与分析
第3.2~3.5节已经对基于形状信息、基于频率信息、基于上下文信息以及基于信息融合的4类分类方法分别开展了对比和分析。本节将进一步从上述4类方法中筛选更具性能优势的方法进行对比和分析, 从而整体地展示和分析TSC领域的发展现状。
-
(1) 由于基于形状信息的分类方法得到了最为广泛的研究, 在这类方法中, 本节选择TSN、Proximity Forest和TSBF 3种传统方法, 以及InceptionTime-5、ResNet和FCN 3种深度学习方法;
-
(2) 在基于频率信息的分类方法中, 本节选择WaveletsFCN和WEASEL;
-
(3) 在基于上下文信息的分类方法中, 本节选择MS-RP-Inception、MS-RP-FCN以及LPS;
-
(4) 在基于信息融合的分类方法中, 本节选择HIVE-COTE以及TS-CHIEF。
从图 19的实验结果中可以发现, 对于传统方法, 基于单一分类信息的方法(TSN, Proximity Forest, TSBF, WEASEL, LPS)在分类精度上难以与信息融合的方法(HIVE-COTE, TS-CHIEF)竞争。然而, 即使深度网络仅从单一表示中提取分类信息, 这些工作依然展现出了很强的竞争力。
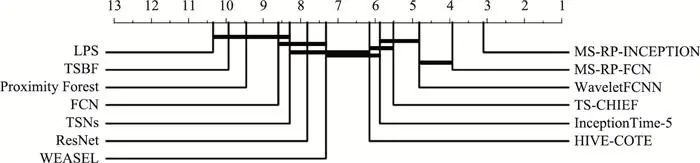
图19 不同TSC方法的关键区别图
如果说基于信息融合的方法从“宽度”上拓展了分类信息, 神经网络则提升了分类信息的“深度”。对过去取得成功的传统方法稍作总结, 可以发现这些方法往往具备平移不变性、局部信息发掘能力以及高效的手工特征等共性优点, 这些优势对TSC任务的重要意义已经得到了广泛验证[6]。幸运的是, 以CNN为代表的深度学习方法几乎全部具备了上述优点, 并在分类特征的提取能力上更胜一筹, 这些因素是深度学习在TSC领域取得成功的主要原因。考虑到基于信息融合的方法以及深度学习在TSC领域取得的成功, 一种思路是利用深度网络从序列数据的多种变换表示中提取和融合分类信息。然而, 哪些变换表示更适合与深度网络相结合, 如何将这些变换“网络化”从而形成“端对端”的网络结构, 这些问题仍需探索。
3.7
TSC方法在不同应用领域的性能对比与分析
为了分析现有分类方法在不同现实应用领域的表现, 本节从85个UCR数据集中提取出4种主要类别, 分别是图像轮廓类数据集、传感器类数据集、电气设备类数据集以及人体动作类数据集。在这些数据集上, 两组分类方法的对比实验如下。
-
(1) A组分类方法由WCDTW[23, 113]以及COTE的两个组件分类器PS和ACF[82]组成, 这3种方法分别基于形状信息、频率信息和上下文信息进行分类, 且在85个UCR数据集上的分类精度没有显著差异;
-
(2) B组分类方法由第3.6节中的13种分类方法组成。
-
从物理意义出发, 本文作出的假设是, 基于形状信息的方法在图像轮廓类数据集上占据优势; 基于频率信息的方法在具有大量噪声和重复模式的传感器类、电气设备类数据集上占据优势; 基于上下文信息的方法在人体动作类数据集上占据优势, 因为不同的动作片段在时间上的关联是重要的分类依据。
从图 20~图 23的实验结果中可以发现, A组方法在图像轮廓类、电气设备类以及人体动作类数据集上的表现符合预期假设, 但这种规律并不明显, 因为在这3类数据集上, A组方法的整体分类精度没有显著差异。然而, A组方法在传感器类数据集, B组方法在全部4类数据集上的表现不符合预期假设。这些现象说明, 大多数TSC任务并不严重倾向于某一种分类信息, 这可能是由于大多数分类任务所面对的困难往往是多样化的。
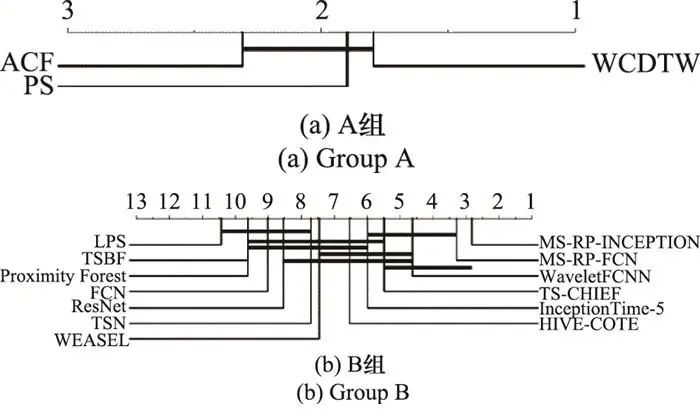
图20 两组分类方法在图像轮廓类数据集的关键区别图

图21 两组分类方法在传感器类数据集的关键区别图
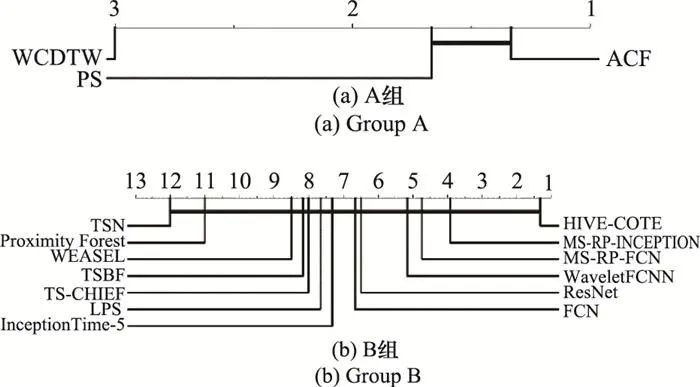
图22 两组分类方法在电气设备类数据集的关键区别图
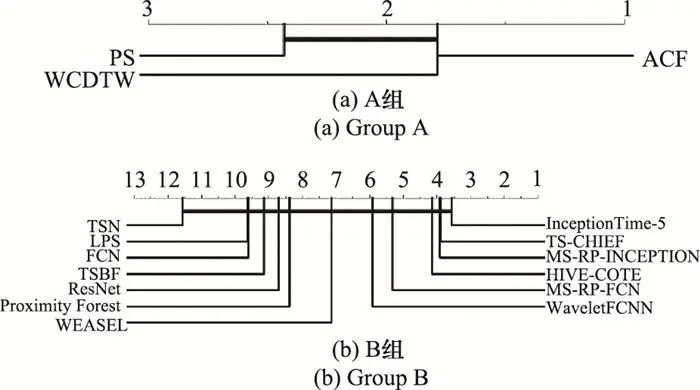
图23 两组分类方法在人体动作类数据集的关键区别图
另外一个发现是, 基于信息融合的方法和基于深度学习的方法在上述4种类型的数据集上均取得了较好的分类效果。这些现象不仅进一步验证了融合多种信息对TSC任务通常是有益的, 同时也证明了深度学习对于TSC任务的良好泛化性能。
4 未来研究方向
4.1
在线分类技术
现实世界的诸多TSC应用, 例如人体动作识别、工业自动控制, 通常需要以数据流的形式, 在算力有限的移动平台上开展在线分类, 这对算法的实时性提出很高的要求。然而, 目前效果较好的分类方法因计算复杂度较高而很难在现实应用中部署。因此, 未来的研究方向是在不显著降低分类精度的基础上, 大幅降低分类方法的计算量, 从而满足在线分类的需求。此外, 对于某些需要在线学习的分类任务[114], 在算法轻量化之余, 如何应对数据流的“概念漂移”问题[115-116], 尚需进一步的研究。
4.2
数据扩充技术
TSC算法的性能很大程度上依赖于大量的训练数据以避免过度拟合。然而, 对于许多现实应用, 例如临床医学、电气设备故障诊断, 相关数据难以获取。因此, 数据扩充技术成为分类算法在这些应用中取得成功的关键因素之一。然而, 正如第2.5节所述, 当前的数据扩充方法存在泛化性能差、解释性不强以及缺乏统一评价标准等缺陷。这些缺陷严重限制了数据扩充在TSC中的成功应用。因此, 序列数据增强技术将是一个值得关注的未来方向, 这方面的工作虽已起步, 但面临的挑战仍然很大。
4.3
基于无监督学习的特征表示技术
在大数据时代, 现实世界中的诸多应用虽然产生了大量的序列数据, 但是这些序列数据通常很不直观, 导致类别标注工作困难。由于标注数据不足, 大量的未标注数据需要得到有效利用。新近的机器学习方法通过无监督学习和数据增强技术从大量未标注数据中学习通用的特征表示, 然后借助有限的标注数据对特征表示进行微调。这种思路在计算机视觉和自然语言处理领域已经取得了广泛成功[117-120], 但在TSC领域还未得到充分探索。因此, 如何借助大量未标注序列数据以无监督的方式学习有效的特征表示, 从而辅助提升有监督学习的性能, 将是未来非常值得关注的方向之一。
4.4
算法的可解释性
可解释性指人类对算法内部机制和输出决策的理解。在实际应用中, 虽然算法的性能指标更值得关注, 但较好的可解释性有利于更加透明地了解模型做出的决策, 从而有效地评估模型在不同场景下的可靠性, 进而支撑对模型的改进。与图像数据相比, 序列数据并不直观, 尽管以Shapelets为代表的可视化技术致力于提升分类算法的可解释性, 然而, 这些技术仍不成熟。此外, 以深度学习为代表的新方法具备明显的黑箱属性, 这些因素为TSC算法的可解释性带来挑战。因此, 增强分类算法的可解释性将是一个值得关注的未来方向, 也是TSC领域的难点之一。
4.5
传统范例启发的深度网络设计
尽管深度学习在TSC领域已取得初步成功, 然而现有工作仅引入了计算机视觉领域的经典网络结构或成熟网络模块, 在网络结构设计方面缺乏对序列数据特性的思考。借助对序列数据的深入理解, 传统分类方法做出了大量的经典手工设计, 这些思想可以启发深度网络的设计。例如, 考虑到一般的卷积核很难适应数据的形状扭曲, 新近工作引入弹性度量的思想有效增强了网络对扭曲形变的适应能力。将传统方法的思想融入深度网络, 有利于增强网络对数据的适应能力, 进而提升网络的分类性能和鲁棒性, 是未来非常值得研究的方向之一。
5 结论
本文对单变量TSC方法进行了综述。首先, 现有的分类方法被分为基于形状信息、基于频率信息、基于上下文信息以及基于信息融合4种类别, 进而分别得到了介绍; 然后, 作为分类算法成功应用的关键因素之一, 序列数据增强也在本文中得到了较为系统的回顾; 最后, 为了对比不同的分类算法, 本文开展了广泛的实验, 并根据实验结果进行了较为深刻的讨论。此外, 本文对单变量TSC领域的下一步研究方向进行了总结和展望。
本文仅用于学习交流,如有侵权,请联系删除 !!