梳理了前面三角基本概念,单位制,扇形与弧长公式,相信大家对三角的学习有了一个好的开始,要想真正的理解三角函数的内涵,还需要从一些口诀来入手,今天我们就来谈谈三角函数和诱导公式;
第一、三角函数的定义
三角函数的定义分初中(锐角三角比)高中(任意角三角函数),不同的学习阶段,对应不同的领悟层次需要。高中阶段主要研究的是正余弦正切函数,因此这三者定义以及函数图像及性质需要完全透彻的理解。
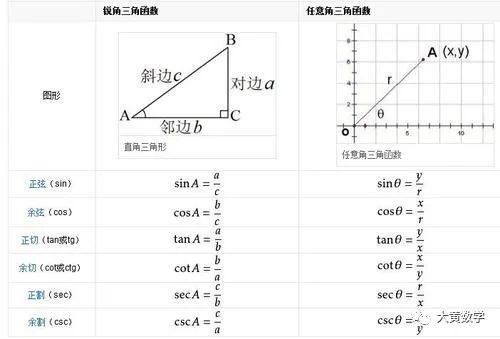
这些三角函数值在各个象限的符号如下图所示,
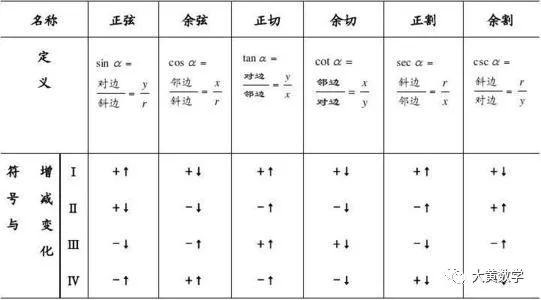
记忆的过程中可以结合三角函数函数线的定义以及动态来观察角α变化的过程中三角函数线的增长趋势。
第二、三角函数线
角α的三角函数值可以用单位圆的有向线段表示:sinα=MP,cosα=OM,tanα=AT.
有向线段MP,OM,AT分别叫做角α的正弦线,余弦线,正切线。
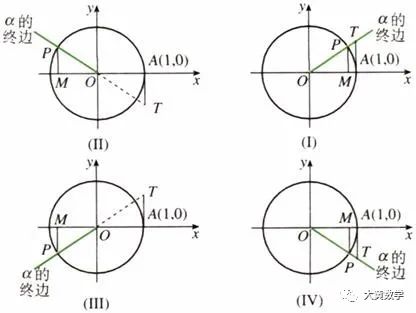
对于三角函数线的认知,我们需要关注以下几点:
(1)结合象限角以及有向线段在各个区间内分别讨论,而且需要注意三角函数线中的字母顺序不可颠倒,与坐标轴方向一致的有向线段为正,此时相应的三角函数值为正,与坐标轴方向相反的有向线段为负,对应的三角函数值为负。
(2)当角α的终边在x轴上时,正切线、正弦线变为一个点,角α的终边在y轴上时,余弦线变为一个点,正切线不存在。
(3)若果01。
第三、同角三角基本关系式
针对同一个角,结合三角比的定义,我们会发现,他有如下三种关系:

针对上述正六边形,结合6个三角比,我们借助:“上弦,中切,下割,左正,右余,中间1”,这十三字,我们可以很快做好定位,不清楚的同学,可以评论区里留言。
具体如何应用这正六边形辅助记忆呢?
首先我们来看平方关系,上图3个红色阴影部分,大家可以视为3个倒三角,上底边的2个三角比的平方之和等于下底角的平方。
其次我们来看商数关系,看相邻三点,如下图,再结合上图,无论ABC,还是ABF,底边上的2个端点之任意一个端点,都等于中间顶点去除另外一个底点,如:tanα=sinα/cosα,cosα=sinα/tanα,secα=tanα/sinα,cscα=secα/tanα等等;
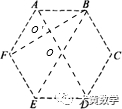
最后我们再看倒数关系,我们来找正六边形的对角线,对角线的两个端点的乘积就是中间1,构成了我们的倒数关系。
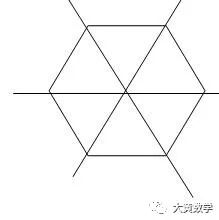
以上3个点,我们也可以用一段话来诠释:
对角线上两函数之积为1,任一角的函数等于与其相邻的两个函数的积,阴影三角形,顶角的两个函数的平方和等于底角函数的平方。
熟悉了同角三角关系式,在应用的过程中,我们还需要注意以下几点:三角函数值间的知一求二,或者求式子的值;化简三角函数式,证明三角恒等式等等。
第四、诱导公式:奇变偶不变,符号看象限
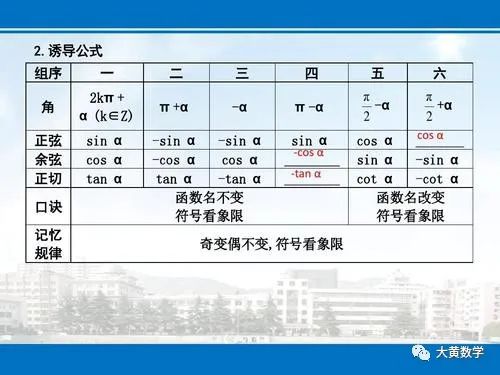
看了上图的表格,相信大家依然懵懂,不要紧,我们看看这个
奇和偶,他是针对π/2,而言的,符号看的是左边原始式子,对于α,无论大小,均视为锐角,
了解了这些,相信大家对于以下式子理解起来倍感轻松。

最后就诱导公式在强调一下这个变,指的是正余弦互变,正余切互变。
第五、学法指导
我们在学了这些知识之后,针对他们的题型主要有如下三种:
第一、求值题型,已知一个角的一个三角函数值,求这个角的其他三角函数值;
这类问题,我们需要关注,角的象限或者终边位置已知,只有一解,角的象限或者终边需要判断;也或者,角的三角函数值含有字母,亦或是另一角的三角函数来表示,我们的解法是合理选择公式,一般思路是按照:“倒-平-倒-商-倒”的顺序很容易求解;在开平方的时候,应注意“±”的取舍,有时根据需要分类讨论。
第二、化简题型,目的是简化运算,要求项数尽量少,次数尽量低,尽量不含分母,尽量不带根号,尽量为数值。
以上是原则要求,需要关注的是,化简过程中,不要忽视三角函数的定义区间。
第三、证明题型,本质上是三角恒等式。
常用方法是:
1、从一边开始,证的另一边,由繁到简。
2、左右归一,证明左右两边都等于同一个式子。
3、凑合法,针对题设与结论间的差异,有针对性的变形,以消除差异,即化异为同。
4、比较法,即证明“左边-右边=0”,或者“左边÷右边=1”
5、分析法,从被证的等式出发,逐步探求使等式成立的充分条件,一直到已知条件或者明显的事实为止,就可以断定原等式成立。
常用的技巧:
1、负角化正角,大角化小角,化异为同,常用诱导公式;
2、切割化弦,弦切互化;
3、1的代换,1=sin²α+cos²α=sec²α-tan²α=csc²α-cot²α=tanπ/4;
4、消元和降次;
5、sinα±cosα、sinαcosα,三个式子中,已知其中一个式子,可求其他两个式子,他隐藏一个条件是:弦的平方和为1。
以上是任意角的三角函数与诱导公式,熟练记忆透彻理解,就在这些口诀上和要点上,相信大家熟读以上,必定会为三角的学习奠定坚实的基础。加油!
就以上知识,大家不清楚的地方欢迎大家评论区留言,大黄必将竭尽全力为您解答。感谢!

