引言
最近碰到一个项目需要用到PID控制算法,于是在网上找了一些资料学习了一下,发现网上对于PID算法的Matlab仿真方面的内容比较少,所以我就把我自己所学习到的内容分享给大家。本次博文主要介绍了位置式和增量式PID控制算法的原理和Matlab的仿真分析。
1、模拟PID控制算法
在工程实际中,应用最为广泛的调节器控制规律为比例、积分、微分控制,简称PID控制,又称PID调节。PID控制器的基本结构如下图所示,G(s)为被控对象的系统传递函数。
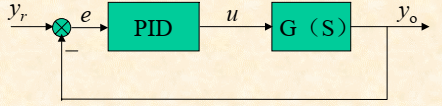
PID控制算法可分为三种,分别是P调节算法(比例调节算法),PI调节算法(比例-积分调节算法)和PID调节算法(比例-积分-微分调节算法),下面从模拟领域来介绍一下以上三种算法的数学原理。
- P调节算法
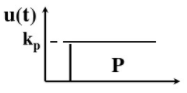
比例控制是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。偏差一旦产生,控制器立即就发生作用即调节控制输出,使被控量朝着减小偏差的方向变化,偏差减小的速度取决于比例系数Kp, Kp越大偏差减小的越快,但是很容易引起振荡,尤其是在迟滞环节比较大的情况下, Kp减小,发生振荡的可能性减小但是调节速度变慢。但单纯的比例控制存在稳态误差不能消除的缺点,这里就需要积分控制。P调节算法的控制规律和阶跃响应如下图所示:
![]()
- PI调节算法
在积分控制中,控制器的输出与输入误差信号的积分成正比关系。对一个自动控制系统,如果在进入稳态后存在稳态误差,则称这个控制系统是有稳态误差的或简称有差系统。为了消除稳态误差,在控制器中必须引入“积分项”。积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。因此,比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。实质就是对偏差累积进行控制,直至偏差为零。积分控制作用始终施加指向给定值的作用力,有利于消除静差,其效果不仅与偏差大小有关,而且
还与偏差持续的时间有关。PI调节算法的控制规律和阶跃响应如下图所示:


- PID调节算法
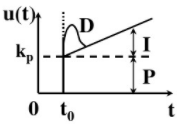
在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。其原因是由于存在有较大惯性组件(环节)或有滞后组件,具有抑制误差的作用,其变化总是落后于误差的变化。解决的办法是使抑制误差的作用的变化“超前”,即在误差接近零时,抑制误差的作用就应该是零。这就是说,在控制器中仅引入“比例”项往往是不够的,比例项的作用仅是放大误差的幅值,而目前需要增加的是“微分项”,它能预测误差变化的趋势,这样,具有比例+微分的控制器,就能够提前使抑制误差的控制作用等于零,甚至为负值,从而避免了被控量的严重超调。所以对有较大惯性或滞后的被控对象,比例+微分(PD)控制器能改善系统在调节过程中的动态特性。它能敏感出误差的变化趋势,可在误差信号出现之前就起到修正误差的作用,有利于提高输出响应的快速性,减小被控量的超调和增加系统的稳定性。但微分作用很容易放大高频噪声,降低系统的信噪比,从而使系统抑制干扰的能力下降。PID调节算法的控制规律和阶跃响应如下图所示:

2、数字PID控制算法
要想让PID算法投入到实际的工业应用中,就必须将其离散化,然后借助如DSP,FPGA等处理器件来完成,因此模拟PID算法就变成了数字PID算法,数字PID算法又分为两大类,分别是位置式PID算法和增量式PID算法。
- 位置式PID算法
模拟PID到数字PID的基本变换过程如下图所示。


我们根据位置式PID的基本原理,运用Matlab做了一个简单的算法仿真。
% 位置式PID算法仿真
clear;
clc;
%% 参数定义
Ts = 1e-3;% 采样时间
e_sum = 0;% 多次误差和
% PID参数(可根据实际情况调节)
kp = 0.32;% 比例
ki = 0.15;% 积分
kd = 0.12;% 微分
%% 建立被控系统
% 假设被控对象的系统传递函数为0.88/(0.05s + 1.5)
s_sys = tf(0.88,[0.05 1.5]); % 根据传递函数建立被控系统的模型
z_sys = c2d(s_sys,Ts,'z'); % 拉氏变换-->z变换
[m,n] = tfdata(z_sys,'v');
%% 开始PID控制
T = 2000;% 设置仿真运行时间
r = 800;% 期望输出值
% 预先分配内存
u = zeros(1,T);% PID输出初始值
y = zeros(1,T);% 被控系统响应输出
e = zeros(1,T);% 误差信号
for k=2:1:T
y(k) = -n(2)*y(k-1) + m(1)*u(k) + m(2)*u(k-1);% 计算被控系统输出
e(k) = r - y(k); % 计算误差
u(k) = kp*e(k) + ki*e_sum + kd*(e(k)-e(k-1)); %根据误差调整PID控制量输出
e_sum = e_sum+e(k);% 计算多次误差和
end
% 绘制过渡过程的曲线
t = 1:1:T;
figure('Color','White');
plot(t,y,'r-','LineWidth',1.2);
title('pid-pos')
xlabel('t');
ylabel('y');
grid on;
set(gca,'FontSize',12,'LineWidth',1.2,'Fontname', 'Times New Roman','FontWeight','Bold')
仿真的过渡过程曲线如下图所示。

- 增量式PID算法
模拟PID到数字PID的基本变换过程如下图所示。

![]()
我们根据增量式PID的基本原理,运用Matlab做了一个简单的算法仿真。
% 位置式PID算法仿真
clear;
clc;
%% 参数定义
Ts = 1e-3;% 采样时间
% PID参数(可根据实际情况调节)
kp = 0.32;% 比例
ki = 0.15;% 积分
kd = 0.12;% 微分
%% 建立被控系统
% 假设被控对象的系统传递函数为0.88/(0.05s + 1.5)
s_sys = tf(0.88,[0.05 1.5]); % 根据传递函数建立被控系统的模型
z_sys = c2d(s_sys,Ts,'z'); % 拉氏变换-->z变换
[m,n] = tfdata(z_sys,'v');
%% 开始PID控制
T = 2000;% 设置仿真运行时间
r = 800;% 期望输出值
% 预先分配内存
u = zeros(1,T);% PID输出初始值
y = zeros(1,T);% 被控系统响应输出
e = zeros(1,T);% 误差信号
d_u = zeros(1,T);% PID输出增量
for k=3:1:T
y(k) = -n(2)*y(k-1) + m(1)*u(k) + m(2)*u(k-1);% 计算被控系统输出
e(k) = r - y(k); % 计算误差
d_u(k) = kp*(e(k)-e(k-1))+ki*e(k)+kd*((e(k)-e(k-1))-(e(k-1)-e(k-2)));% 根据误差获取PID增量
u(k) = u(k-1) + d_u(k);% 根据PID增量计算PID控制输出
end
% 绘制过渡过程的曲线
t = 1:1:T;
figure('Color','White');
plot(t,y,'r-','LineWidth',1.2);
title('pid-incre')
xlabel('t');
ylabel('y');
grid on;
set(gca,'FontSize',12,'LineWidth',1.2,'Fontname', 'Times New Roman','FontWeight','Bold')
仿真的过渡过程曲线如下图所示。

后续我还将推出整个PID算法的FPGA实现,敬请关注。