在信号或者图像的降噪研究中,很多学者采用高斯白噪声添加到干净的样本中,来模拟含有噪声的样本,并以此来验证提出模型的降噪效果(比如降噪自编码器——Denoising Autoencoder)。有一次投稿,一个审稿人问为什么采用高斯白噪声? 如何保证添加噪声后,样本有指定的信噪比(Signal to Noise Ratio)?
对于第一个问题,我自己一时回答不上来,于是就去网上查找资料。我相信这两个问题也是初次接触降噪研究的人需要了解的,所以将这两个问题的答案记录如下,首先我们来回答第二个问题。
1、如何在样本中添加噪声,使样本具有指定的信噪比
1.1 合成具有指定信噪比的噪声样本
首先,我们要知道信噪比的定义。信噪比是指信号功率和噪声功率比值的对数,如下式所示:
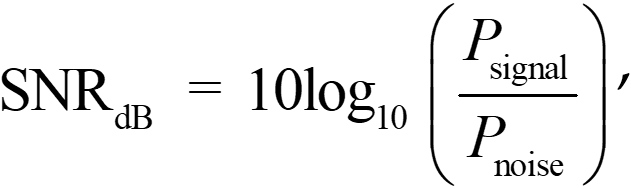
通常,我们获取的信号是离散的,而且可以直接计算信号的功率。假设我们有一离散信号为 S= {s1, s2, …, sn},那么,可以计算出信号功率 P_signal 为:
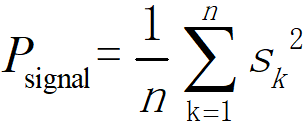
有了信号功率后,假如我们想要添加完噪声后样本的信噪比为SNR(比如-2 dB,0 dB …),那么,我们可以通过这两者计算出噪声的功率:
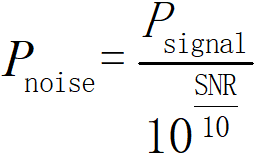
获得噪声的功率之后,我们可以先生成一个标准高斯分布(均值为0,标准差为1)的噪声序列(和信号长度一样),然后再通过转换得到我们最终想要的高斯噪声。在Python程序中,通过Numpy.random 的randn,我们可以生成一个标准高斯分布序列(在matlab 中也是如此,用 randn 函数产生标准正态分布)。接下来,我们用python 程序来说明获得我们想要的噪声的过程。
import numpy as np
def gen_gaussian_noise(signal,SNR):
"""
:param signal: 原始信号
:param SNR: 添加噪声的信噪比
:return: 生成的噪声
"""
noise=np.random.randn(*signal.shape) # *signal.shape 获取样本序列的尺寸
noise=noise-np.mean(noise)
signal_power=(1/signal.shape[0])*np.sum(np.power(signal,2))
noise_variance=signal_power/np.power(10,(SNR/10))
noise=(np.sqrt(noise_variance)/np.std(noise))*noise
return noise我们用程序来验证一下,假设我们有一个样本,样本为正弦波形,总共包含2000个点:
x=np.linspace(1,6,2000)
signal=np.sin(x)我们在该样本上添加高斯噪声,使得添加噪声后的样本的信噪比为-2 dB,程序如下:
noise = gen_gaussian_noise(signal,-2)获得我们想要的噪声之后,合成含噪样本也很简单,直接将原始信号和噪声相加即可:
noisy_signal=signal+noise至此,我们已经合成了信噪比为 -2 dB 的含噪样本。
1.2 验证噪声样本的信噪比
在上文中,我们已经合成了信噪比为 -2 dB 的正弦信号,接下来我们来验证一下,合成信号的信噪比是否确实为 -2 dB:
def check_snr(signal,noise):
"""
:param signal: 原始信号
:param noise: 生成的高斯噪声
:return: 返回两者的信噪比
"""
signal_power=(1/signal.shape[0])*np.sum(np.power(signal,2))# 0.5722037
noise_power=(1/noise.shape[0])*np.sum(np.power(noise,2)) # 0.90688
SNR=10*np.log10(signal_power/noise_power)
return SNR
SNR= check_snr(signal,noise)
print (SNR) # 输出 -1.999999999999991 dB,由于计算机数值计算的问题,存在极小的误差。可以看出,生成的噪声符合我们的要求。
2 为什么降噪研究采用高斯白噪声?
关于这部分的问题,我觉得知乎上的 Bihan Wen 的回答非常具有参考价值,下文均引自他的回答,原链接如下:
https://www.zhihu.com/question/67938028
谢邀。这个问题很好,我认为做降噪的同学都应该思考一下。
然而,我觉得已有的回答没有答到这个问题的本质。我认为题主的问题,需要通过以下三个子问题来说明:
为什么要做仿真噪音synthetic noise的实验?在所有的synthetic noise里,为什么大家都用高斯白噪声,而不太常用其他distribution的噪声?基于synthetic noise,比如高斯噪音的算法,可以适用于真实噪音吗?
以下回答,我尽量不引用论文,不安利自己的工作,先说结论,后说论据,以方便阅读。
问题一:Why synthetic noise?
先说结论:相对于real noise,用synthetic noise的好处是便于分析问题/设计算法,便于量化和评价算法效果。
便于对降噪问题的分析/算法的设计:降噪的本质是对数据本身的重建,以起到排除污染(corruption)的作用。这里面涉及到需要对(1)数据,(2)污染(噪音)的模型和分析。数据的模型就是我们一般常用的那些,比如稀疏表达(sparse coding),统计(probabilistic),低秩(low-rankness),collaborative filtering之类的。这些都是基于一定的数学假设。说穿了,事实上没不存在对数据100%精确的model,或者所谓的true model。再来说噪音模型,我们一般把noise这种污染定义为一个additive或者multiplicative的随机变量。那么这个随机变量的随机分布是什么?如果知道了这个,我们就可以设计出对应的合理的算法。
那么如果是real noise,他是什么分布呢?没有人知道,因为real就意味着未知。噪音可以是unstructured的,也可以是structured的。real的数据里面的噪音,可以是consistent的,也可以是变动的。甚至一幅图,一个视频里的real noise在不同位置都是不一样的。那这种情况下的问题分析就是极难的,或者说这个问题本身就是untrackable的,not well defined的。
所以科研或者工程设计里面,都会对这类问题做出合理的假设,比如这里的:噪音是高斯白噪声。基于这个假设再来分析问题。
便于量化和评价算法效果:评价一个降噪算法的效果,需要采用一定的评价标准(metric)。我们一般把评价标准分为客观(objective)和主观(subjective)的:
客观标准很好理解:给我一个数学计算方式,算出这个降噪过后的数据,到底有多好。这样做清晰明了,一般没有什么好争议的。常见的这样的metric有Peak Signal-to-Noise Ratio (PSNR),Mean Square Error(MSE),Structured Similarity(SSIM),等等。你经常可以在降噪论文里面看到这三个家伙的身影。他们这些metric的绝对数值的高低,直观地反应方法效果的好坏。
虽然我知道也有一些工作,试着propose一些不需要ground truth的objective quality metric,但最常用的这类经典metric无一例外地需要图片的无噪音真实值(ground truth)作为参考。如果你是使用仿真噪音,你自然是有ground truth的。但如果是真实噪音,你确一般不知道ground truth是什么。
所以一般对于真实噪音的降噪实验,我们都只好算法一些subjective的metric:让人眼来辨认降噪出来的图效果是否好。这不同的人,可能对图的喜好也会不一样,这样就经常会产生评价的个体差异,产生争议。就算想要组织一大批人来做测试,成本会很高,不利于科研的高效性。
问题二:Why Gaussian noise?
先说结论:相比于其他的synthetic noise distribution,高斯噪音确实有他的合理性。在真实噪音的噪音源特别复杂的时候,高斯噪音可能算是最好的对真实噪音的模拟。
其实不光是深度学习的降噪算法,传统方法(好吧,自从有了深度学习以后,什么sparse coding,GMM,low-rank,collaborative filtering都变成传统方法了…)也大多喜欢用高斯白噪声来做仿真实验。那么大家不约而同地都玩儿高斯噪音可能有背后的原因。我觉得这个可能才是题主最关心的问题。
那这里的答案就是,采用高斯噪音,是为了更好地模拟未知的真实噪音:在真实环境中,噪音往往不是由单一源头造成的,而是很多不同来源的噪音复合体。假设,我们把真实噪音看成非常多不同概率分布的随机变量的加合,并且每一个随机变量都是独立的,那么根据Central Limit Theorem,他们的normalized sum就随着噪音源数量的上升,趋近于一个高斯分布。
基于这种假设来看,采用合成的高斯噪音,是在处理这种复杂,且不知道噪音分布为何的情况下,一个既简单又不差的近似仿真。
问题三:Can it work for real noise?
先说结论:在高斯噪音试验下效果的算法,不一定在真实噪音下效果也同样地好。这个要看真实噪音具体长啥样,还要看算法本身的设计是否对噪音分布有一定的鲁棒性。
在搞清楚了问题一和二之后,相信问题三应该就很好理解了:因为Gaussian noise只是对real noise的一个近似和仿真,没有任何的保证说,设计的算法在处理real noise的时候就一定要表现得同样得好。但由于问题二我们讲了,Gaussian noise test有一定的合理性,所以这类算法在real noise的情况下都会有一定的降噪功用。
最近有一些新的数据库,包括了真实噪音图片以及他们捕捉到的ground truth。我认为这类数据库将会带来一波专注于真实噪音除去的工作。
最后再来说说深度学习,在降噪问题上的特殊性:
深度学习之类算法,模型本身是高度data-driven,而不是rule-based的。换句话说,深度学习算法的设计,或者说网络结构的设计,并不强烈依赖于噪音的概率分布。这对于降噪算法的generalization是很好的。
然而这并不是说,深度学习的降噪算法,是对所有噪音类型通吃的。深度学习算法一般需要supervised training。这样在训练数据上的选择,确实往往依赖于噪音的概率分布:如果我们要做Gaussian noise removal,那训练数据就应该是添加了Gaussian noise的结果。那么如果我们要做真实噪音的denoising,要怎么准备训练数据?你的训练数据的噪音分布,和你的测试数据是一样的吗?这些都没有保证,或者说不一定说是consistent的。
但是我个人看法是,可能相对于传统方法而言,深度学习算法在从一种特定噪音的处理,generalize到未知噪音,鲁棒性应该会更高。虽然没有理论上的证明(深度学习上搞这种证明,臣妾确实办不到…),我们近期的工作也证实了这一点。这一段都是私货,如果有其他大神有对这个更好的看法,欢迎讨论。
3、在样本中添加真实的噪声
假如你想在样本中添加真实的噪声,但是你又没有条件做这样的实验,或者说由于噪声的复杂性,你做的实验同行未必认可。实际上,在工业界有标准的噪声库,比如
NOISEX-92
,其中带有白噪声、办公室噪声、工厂噪声、汽车噪声、坦克噪声等等,在研究中也可以选用合适的噪声叠加到信号中去,但是噪声的采样频率与信号的采样频率往往不一致,需要采样频率的校准。具体的方法请参考
这篇文章
。