本文实现目标:
实现 step1/SeqStack.cpp 中的
SS_IsFull
、
SS_IsEmpty
、
SS_Length
、
SS_Push
和
SS_Pop
五个操作函数,以实现判断栈是否为满、是否为空、求栈元素个数、进栈和出栈等功能。
栈是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算,这一端被称为栈顶。栈既可以采用顺序存储,也可以采用链接存储来实现。下面给出了一种基于顺序存储的栈的实现方案:

如图 1 所示:该栈存储了 4 个元素 {56,77,15,12} ,其中 12 是栈顶元素。
这种实现方案将栈元素存储在一片连续的空间中,栈相关的三个属性元素
data
、
top
和
max
介绍如下:
-
data
: 给出栈存储空间的起始地址; -
top
: 存放栈顶元素的位置编号; -
max
: 指明栈存储空间中最多可存储的数据元素个数。
栈结构的定义(C)
基于
data
、
top
、
max
组织成的栈结构如下所示:
-
struct SeqStack{
-
T* data; // 数据元素指针
-
int top; // 栈顶元素编号
-
int max; // 最大结点数
-
};
为了讨论简单,我们假设栈元素的数据类型为整数:
typedef int T; // 栈元素的数据类型
据此,只要给定指向该结构的一指针 ss ,就可对栈进行进栈出栈操作。
- 进行进栈操作时,新进栈的元素保存在 top+1 位置,进栈后 top 加 1 ,这时的状态则如图 2 所示。

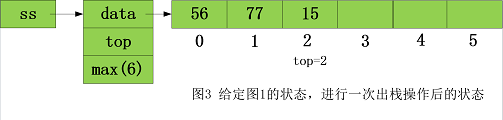
- 进行出栈操作时,将位置编号为 top 的元素出栈,出栈后 top 减去 1 ,这时的状态则如图 3 所示。
顺序栈的操作
以顺序存储的栈为例,我们定义如下操作:
-
创建栈:创建一个最多可以存储 maxlen 个元素的顺序栈。具体操作函数定义如下:
SeqStack* SS_Create(int maxlen)
; -
释放栈空间:释放栈所占用的空间。具体操作函数定义如下:
void SS_Free(SeqStack* ss)
; -
清空一个栈:将栈中元素清空。具体操作函数定义如下:
void SS_MakeEmpty(SeqStack* ss)
; -
判断栈是否为满:若栈为满,则返回
true
,否则返回
false
。具体操作函数定义如下:
bool SS_IsFull(SeqStack* ss)
; -
判断栈是否为空:若栈为空,则返回
true
,否则返回
false
。具体操作函数定义如下:
bool SS_IsEmpty(SeqStack* ss)
; -
求栈元素个数:获取栈元素个数。具体操作函数定义如下:
int SS_Length(SeqStack* ss)
; -
将元素 x 进栈:将 x 进栈,若满栈则无法进栈,返回
false
,否则返回
true
。具体操作函数定义如下:
bool SS_Push(SeqStack* ss, T x)
; -
出栈:出栈的元素放入 item 。若出栈成功(栈不为空),则返回
true
;否则(空栈),返回
false
。具体操作函数定义如下:
bool SS_Pop(SeqStack* ss, T &item)
; -
获取栈顶元素:获取栈顶元素放入 item 中。若获取失败(空栈),则返回
false
,否则返回
true
。具体操作函数定义如下:
bool SS_Top(SeqStack* ss, T & item)
; -
打印栈中元素:从栈底到栈顶打印出所有元素。具体操作函数定义如下:
void SS_Print(SeqStack* ss)
。
相信大家对于栈已经有了很深的理解,下面给出C/C++语言实现的代码(仅供参考):
#include <stdio.h>
#include <stdlib.h>
#include "SeqStack.h"
/*创建一个栈*/
SeqStack* SS_Create(int maxlen)
{
SeqStack* ss=(SeqStack*)malloc(sizeof(SeqStack));
ss->data=(T*)malloc(maxlen*sizeof(T));
ss->top=-1;
ss->max=maxlen;
return ss;
}
/*释放一个栈*/
void SS_Free(SeqStack* ss)
{
free(ss->data);
free(ss);
}
/*清空一个栈*/
void SS_MakeEmpty(SeqStack* ss)
{
ss->top=-1;
}
/*判断栈是否为满*/
bool SS_IsFull(SeqStack* ss)
{
if (ss->top==ss->max-1)
return true;
else
return false;
}
/*判断栈是否为空*/
bool SS_IsEmpty(SeqStack* ss)
{
if (ss->top==-1)
return true;
else
return false;
}
/*获取栈元素个数*/
int SS_Length(SeqStack* ss)
{
return ss->top+1;
}
/*将x进栈,满栈则无法进栈(返回false)*/
bool SS_Push(SeqStack* ss, T x)
{
if (ss->top==ss->max-1)
return false;
else
{
ss->top++;
ss->data[ss->top] = x;
return true;
}
}
/*出栈,出栈的元素放入item,空栈则返回false*/
bool SS_Pop(SeqStack* ss, T &item)
{
if (ss->top==-1)
return false;
else
{
item = ss->data[ss->top];
ss->data[ss->top] = NULL;
ss->top--;
return true;
}
}
/*获取栈顶元素放入item中,空栈则返回false*/
bool SS_Top(SeqStack* ss, T & item)
{
if (SS_IsEmpty(ss)) {
return false;
}
item = ss->data[ss->top];
return true;
}
/*从栈底到栈顶打印出所有元素*/
void SS_Print(SeqStack* ss)
{
if (SS_IsEmpty(ss)) {
printf("stack data: Empty!\n");
return;
}
printf("stack data (from bottom to top):");
int curr=0;
while(curr<=ss->top) {
printf(" %d", ss->data[curr]);
curr++;
}
//printf("\n");
}
通过以上代码,我们可以实现对于顺序存储的栈的一系列基本操作,并可以以此为基础去解决一些相关的实际问题。
欢迎大家留言评论指出一些地方的改进方法!