百度2019年暑期实习生面试的一道大题,就是解释相机成像的原理以及相机的内参矩阵和外参矩阵,以及相机拍摄中会产生什么畸变以及畸变的矫正方法。
参考资料:
https://blog.csdn.net/liuqinglong110/article/details/42076895
http://www.cse.psu.edu/~rtc12/CSE486/lecture12.pdf
http://www.cse.psu.edu/~rtc12/CSE486/lecture13.pdf
下面按照给出的PPT详细解释。相机成像原理中涉及到4个坐标系的转换,分别是:
| 维度dimension | 含义 | |
| 世界坐标系(world coordinate) | 3D,(U,V,W) | 世界坐标系可以由用户任意给定,表示在真实的3D物理世界中给定一个坐标系以描述物理世界中的3D点,世界坐标系通常以所感兴趣的物体object为中心建立(意味着所感兴趣的物体不同,建立的世界坐标系位置也不一样) |
| 相机坐标系(camera coordinate) | 3D,(X,Y,Z) | 相机坐标系由相机的位置唯一确定,一旦相机的光轴和光心确定后,相机坐标系的3个轴就给定了,它也是用来描述真是物理世界中的点在相机坐标系下的坐标 |
| 成像坐标系/感光器件坐标系(film coordinate) | 2D ,(x,y) | 成像坐标系由相机的成像平面唯一确定,表示将相机坐标系中的点(3D)投影到感光器件上成像得到2D坐标点 |
| 像素坐标系(pixel coordinate) | 2D ,(u,v) | 进行图像处理算法时用到的图像所在的2D像素坐标系 |
在将世界坐标系中的3D真实点转换到通常进行图像处理时所使用的以像素为单位的2D图像上,通常的前向投影过程如下:
(1)通过外参矩阵(包括旋转矩阵R和平移矩阵T)将世界坐标系中的点转换到相机坐标系中。
(2)通过相机内参f:相机的焦距(成像平面到光心的距离,在相机主轴上计算)参数,将相机坐标系中的点转换到成像坐标系上。
(3)通过相机内参Ox,Oy(平移,从成像坐标系的中心点平移到像素坐标系的中心点上)和Sx、Sy(对于成像平面/感光器件成像后的图像进行的采样,表示x和y轴方向上的采样率),将成像坐标系转换到图像像素坐标系上。





一、世界坐标系到相机坐标系(相机外参R和T)





那么平移矩阵和旋转矩阵中的数值如何确定呢?先假设已经将世界坐标系的原点和相机坐标系的原点平移到了同一点,接下来只考虑旋转变换。假设在世界坐标系中有一个点的坐标是(1,0,0),它在相机坐标系中的点的坐标是(a,b,c),则旋转矩阵的第一列就表示在世界坐标系中坐标为(1,0,0)的点投影到相机坐标系后的坐标,同理:旋转矩阵的第2列表示在世界坐标系中坐标为(0,1,0)的点投影到相机坐标系后的坐标.


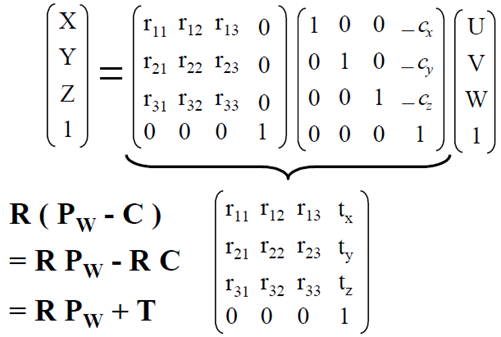
从世界坐标系中的点转换到相机坐标系中的变换是刚体变换,故而旋转矩阵必然是正交矩阵并且是对称矩阵(转置之后等于原来的矩阵)。这一变换是在相机外部完成的,故而使用的旋转矩阵和平移矩阵中的参数属于相机外参。
tx=-r(11)*c(x)-r(12)*c(y)-r(13)*c(z)
二、相机坐标系到成像坐标系(相机内参f)

从相机坐标系3D到成像坐标系2D,使用的是透视变化 (利用相似三角形原理),注意图中给出的成像平面本身应该在光心O左边的f位置处(才是正确的小孔成像原理),但是这里为了简便就直接对称过来了。


三、成像坐标系到像素坐标系(相机内参Ox,Oy,Sx、Sy)



四、相机成像原理总结



五、相机成像过程中可能发生的畸变