【全文翻译】Composite Adversarial Attacks

复合对抗攻击

1、 Abstract

对抗性攻击是一种欺骗机器学习模型的技术，它提供了一种评估对抗性鲁棒性的方法。在实践中，攻击算法是由人类专家人工选择和调整的，以破坏ML系统。然而，手动选择攻击者往往是次优的，导致对模型安全性的错误评估。本文提出了一种新的过程，称为复合对抗攻击（CAA），用于从32个基本攻击者的候选池中自动搜索攻击算法及其超参数的最佳组合。我们设计了一个搜索空间，将攻击策略表示为一个攻击序列，即前一个攻击者的输出作为后继攻击者的初始化输入。采用多目标NSGA-II遗传算法，以最小的复杂度寻找最强的攻击策略。实验结果表明，CAA在11种不同的防御方式下，以较短的时间（比自动攻击快6倍）击败了10名顶级攻击者，在

∞

l_∞

$l_{\infty}$

,

l_2

$l_{2}$

和无限制的对抗性攻击。

2、Introduction

DNNs 容易受到对手攻击，这种攻击的目的是通过产生不易察觉的扰动样本来愚弄训练有素的模型。这种严重的安全隐患很快引起了机器学习界的广泛关注。通过对对抗样本的深入研究，提出了多种攻击算法来验证对抗的鲁棒性。同时，一些开源工具箱，如Cleverhans1（Papernot et al.2016）、FoolBox2（Rauber、Brendel和Bethge 2017）或AdverTorch3（Ding、Wang和Jin2019）正在开发并集成大多数现有的攻击算法。为方便快捷地攻击模型提供了友好的用户界面。

然而，即使开发了设计良好的工具箱，攻击一个模型仍然需要大量的用户体验或手动调整攻击的超参数，尤其是当我们无法了解目标模型的防御机制时。这种依赖于用户的特性也使得对抗性攻击的工具化变得困难。另一方面，手动选择攻击者有一定的倾向性和次优性。它可能会引起对模型安全性的错误评估，例如，众所周知的错误安全感是梯度模糊，这会导致对基于梯度的攻击的虚假防御。

为了实现更全面、更强的攻击，我们首先提出了通过从一系列攻击算法中搜索有效的攻击策略来实现攻击过程的自动化。我们将此过程命名为复合对抗攻击（CAA）。为了说明CAA的关键思想，图2中给出了一个示例。假设有两种候选攻击方式，即空间攻击（Engstrom et al.2019）和FGSM攻击（Goodfello，Shlens和Szegedy 2014），目标是选择其中一种或多种来组成更强的攻击策略。在图2（b）中，最简单的方法是选择最佳的单个攻击作为最终策略。然而，正如以前的工作（Tram`er和Boneh 2019）所示，单个攻击者总是不够强大和通用。一个更具潜力的解决方案（Croce和Hein 2020）是找到多个攻击者，然后通过不断选择能够成功欺骗模型的最佳输出来集成它们（图2（c））。集成攻击虽然可以获得较高的攻击成功率，但只提供输出级的聚合，没有考虑不同攻击机制之间的互补性。

在这里插入图片描述

在我们的复合对抗攻击中，我们将攻击策略定义为攻击者的串行连接，其中前一个攻击者的输出作为后继攻击者的初始化输入。在图2（d）中，两个攻击者可以生成四种可能的排列。通过使用搜索算法来寻找最佳排列，我们证明了空间攻击之后的FGSM攻击可以获得比它们的集合高26%的错误率。我们政策的好处在于两个方面：1）通过引入身份攻击（即无攻击），我们的CAA可以表示任何单个攻击。集合攻击也可以用CAA的策略集合来表示。因此，CAA是更广义的表述。2）一个强大的攻击可以通过渐进的步骤产生。以前的工作（Suya et al.2020）发现，在优化攻击方面，一些接近决策边界的起点比原始种子更好。类似地，在CAA中，我们使用前面的攻击者创建一个距离原始种子足够远、距离边界足够近的样本，以便后续的攻击更容易找到一个更强的对手样本。

具体地说，CAA是通过包含多个选择和攻击操作顺序的搜索空间来实现的。对于每个攻击操作，有两个超参数，即幅值和迭代步长。我们采用NSGA-II遗传算法（Deb等人，2002）来寻找能够以最高的成功率突破目标模型但复杂度最小的最佳攻击策略。大量实验表明，CAA在两个用例中取得了很好的改进：1）CAA可以直接应用于感兴趣的目标模型上，以找到最佳攻击策略（

CAA_{dic}

$C A A_{d i c}$

）；2）学习策略可以在不同的任务下保持较高的成功率转移到攻击多模型体系结构（

CAA_{sub}

$C A A_{s u b}$

）。我们评估了

CAA_{dic}

$C A A_{d i c}$

和

CAA_{sub}

$C A A_{s u b}$

最近提出的11项关于

∞

l_∞

$l_{\infty}$

,

l_2

$l_{2}$

和无限制设置。结果表明，我们的复合对抗攻击在白盒场景中达到了最新的水平，大大降低了攻击时间开销。

3、Preliminaries and Related work（准备工作和相关工作）

Adversarial Attack

定义和概念

设

∈

[

]

→

∈

F:x∈ [0, 1]^D → z∈ R^K

$F : x \in [0, 1]^{D} \to z \in R^{K}$

是K类图像分类器，其中

x

$x$

是

D

$D$

维图像空间中的输入图像，

z

$z$

代表logits。假设

F

$F$

执行得很好，并且正确地将

x

$x$

分类为它的基本真值标签

y

$y$

。对抗性攻击的目的是找到一个在一定距离度量下接近原始

x

$x$

的对抗性样本

x_{adv}

$x_{a d v}$

，但它会导致模型的错误分类：

（

）

≠

F（x_{adv}）\not=y

$F （ x_{a d v} ） \neq = y$

。

常规对抗样本

常规的对抗样本具有有限的扰动幅度，这通常是通过在输入

x

$x$

周围的

\epsilon

$ϵ$

半径

l_p

$l_{p}$

球内限定扰动来实现的。它可以由

(

)

≠

F(x_{adv})\not=y

$F (x_{a d v}) \neq = y$

受限于

∣

−

∣

≤

||x_{adv}-x||_p≤ λ

$∣ ∣ x_{a d v} - x ∣ ∣_{p} \leq λ$

。快速梯度符号法（FGSM）是一种经典的

∞

l_∞

$l_{\infty}$

对抗式攻击方法沿损失函数梯度方向对原始样本

x

$x$

进行单步更新。使用基于动量的多步优化（Dong et al.2018）或扰动的随机初始化（Madry et al.2017），FGSM有许多改进版本。基于

l_2

$l_{2}$

的攻击，如DDNL2（Rony et al.2019）和C&W（Carlini and Wagner 2017）发现

x_{adv}

$x_{a d v}$

与原始样本的

l_2

$l_{2}$

距离最小。基于

l_1

$l_{1}$

的攻击者保证了扰动的稀疏性，例如EAD（Chen等人，2017）。然而，

l_1

$l_{1}$

攻击在实际攻击环境中并不常用。因此，本文没有在

l_1

$l_{1}$

约束下实现CAA。

无限制对抗样本

无限制对抗性样本是一种新型的不受范数有界小扰动限制的对抗性样本。在这种情况下，攻击者可能会在不更改语义的情况下显著更改输入(Brown等人（2018）首先引入了无限制对抗样本的概念，并提出了一个两人无限制攻防比赛。最近，有许多工作旨在利用生成模型（Song et al.2018）或空间变换（Engstrom et al.2019）构建这种更强的无限制攻击。在本文中，我们还使用最大的搜索空间（总共19次攻击）。我们发现，即使应用非常简单的基本攻击者来形成搜索空间，我们的CAA搜索的策略在不受限制的设置下仍然产生令人惊讶的攻击能力。

Automated Machine Learning

我们的方法受到AutoML及其子方向（如神经结构搜索（NAS）和超参数优化（HPO））的最新进展的启发。在AutoML中，搜索算法用于自动选择算法、特征预处理步骤和超参数。另一个类似的方向是AutoAugment（Cubuk et al.2018），它自动搜索改进的数据增强策略。这些自动化技术不仅使人们摆脱了算法繁琐的过程微调的同时，也大大提高了学习系统的效果和效率。在本文中，我们采用了AutoML中的一些搜索技术，证明了搜索更好的算法和参数也有助于对抗性攻击。

Composite Adversarial Attacks（复合对抗攻击）

Problem formulation（问题描述）

假设我们有一个带注释的数据集

，

{X，Y}

$X ， Y$

和一组带有一些未知超参数的攻击算法。本文将每种攻击算法看作一个操作

∈

[

]

→

∈

[

，

]

A:x∈ [0, 1]^D → x_{adv}∈ [0，1]^D

$A : x \in [0, 1]^{D} \to x_{a d v} \in [0 ， 1]^{D}$

，将输入

x

$x$

转换为图像空间上的对抗性

x_{adv}

$x_{a d v}$

。A在不同的攻击设置下有不同的选择。例如，在白盒对抗攻击中，A直接优化输入

x

$x$

周围

\epsilon

$ϵ$

半径球内的扰动

δ

$δ$

，以使分类误差最大化：

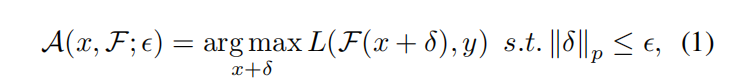
在这里插入图片描述

其中，

L

$L$

通常指交叉熵损失，

∣

||.||_p

$∣ ∣ . ∣ ∣_{p}$

表示

l_p

$l_{p}$

范数，并且

\epsilon

$ϵ$

是

l_p

$l_{p}$

范数的界。

\epsilon

$ϵ$

可以看作

A

$A$

的超参数。此外，还有许多其他攻击设置，例如黑盒攻击（Uesato et al.2018；Andrishchenko等人，2019年），无限制对抗性攻击（Brown等人，2018年）。我们以统一的方式将它们表示为攻击行动。

假设我们有一组基本攻击操作，表示为

A

$A$

={

，

…

A_1，A_2…A_k

$A_{1} ， A_{2} \dots A_{k}$

}，其中

k

$k$

是攻击操作的总数。复合对抗攻击的目标是通过搜索攻击操作的最佳组合和每个操作的超参数，实现对抗攻击过程的自动化，从而实现更一般、更强大的攻击。在这项工作中，我们只考虑攻击算法中两个最常见的超参数：1）攻击幅度

\epsilon

$ϵ$

（也相当于扰动的最大

l_p

$l_{p}$

范数）和2）攻击的优化步骤t。为了限制两个超参数的搜索范围，给出了两个区间：

\epsilon

$ϵ$

∈ [0，

\epsilon_{max}

$ϵ_{m a x}$

]和t∈ [0，

t_{max}

$t_{m a x}$

]，其中

\epsilon_{max}

$ϵ_{m a x}$

和

t_{max}

$t_{m a x}$

是用户预定义的每次攻击的最大幅度和迭代次数。在本文中，我们不搜索攻击步长，因为它与优化步长t有关。相反，所有需要步长参数（如PGD）的攻击都会根据以前的方法修改为无步长版本（Croce和Hein 2020）。因此，可以基于优化步长自适应地改变步长。然后我们可以将策略定义为各种攻击的组合，由N个连续的攻击操作组成：

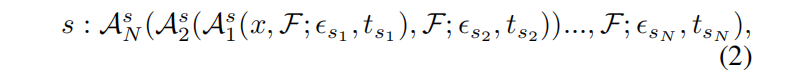
在这里插入图片描述

其中 {

∈

∣

A^s_n ∈ A | n = 1, …, N

$A_{n}^{s} \in A ∣ n = 1, . . ., N$

}是从单独的攻击中采样的攻击者，{

{

\epsilon_{sn}

$ϵ_{s n}$

,

t_{sn}

$t_{s n}$

} |

n = 1, …, N

$n = 1, . . ., N$

}是每个攻击的超参数。结合不同的攻击操作和超参数，我们可以得到上千种可能的策略。

Constraining lp-Norm by Re-projection（重投影约束lp范数）

式2中给出的攻击策略是一种一般形式，对全局扰动没有约束。当攻击序列变长时，每个攻击算法的计算扰动会累积，导致对原始输入的最终扰动变大。为了解决这个问题，我们在两个连续的攻击算法之间插入一个重投影模块。在图3中，重投影模块首先确定先前攻击者上累积的

\epsilon

$ϵ$

是否大于策略的

\epsilon_{global}

$ϵ_{g l o b a l}$

。如果是，则对累积扰动进行剪裁或重新缩放，使

l_p

$l_{p}$

范数在

\epsilon_{global}

$ϵ_{g l o b a l}$

中有界。通过这种修改，我们可以对任何

l_p

$l_{p}$

范数条件使用复合对抗攻击。

在这里插入图片描述

Search Objective（搜索目标）

搜索对象以往的工作通常以攻击成功率（ASR）或鲁棒精度（RA）作为目标来设计算法。然而，这些目标可以以花费更多的时间为代价来实现。例如，最近提出的工程（Gowal等人，2019年；Tashiro 2020）使用随机重启或多目标等技巧，以获得更高的成功率，同时牺牲运行效率。这使得他们的算法非常慢（甚至比一些黑盒攻击更耗时）。在这项工作中，我们强调一个好的和强大的攻击者应该是既有效又高效的。为了达到这个目标，我们设计了两个最小化的目标，即鲁棒精度和复杂性。

接下来，我们将阐述这两个客观条件。第一项RA（鲁棒精度）是目标模型对生成的对抗样本的准确性。这也反映了攻击者的实力。对于第二项复杂度，我们使用梯度评估的次数作为复杂度度量。对于常规攻击算法，梯度求值次数表示攻击算法在攻击过程中计算目标模型梯度的次数，通常等于优化步骤t。因此，我们可以将总体目标函数表述为：

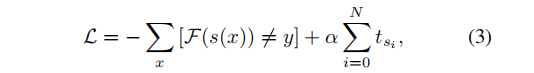
在这里插入图片描述

其中

（

）

s（x）

$s （ x ）$

表示针对输入

x

$x$

的攻击策略的输出，

N

$N$

是攻击策略的长度，

α

$α$

是权衡攻击强度和复杂性的系数。然后，我们可以应用搜索算法，通过最小化目标

L

$L$

，从数千个可能的策略中找到最优攻击策略

∗

s^*

$s^{*}$

：

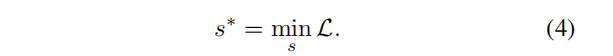
在这里插入图片描述

Search Space（搜索空间）

我们的搜索空间分为两部分：1）搜索攻击操作的选择和顺序；2）搜索每次攻击行动的幅值

\epsilon

$ϵ$

和步数

t

$t$

。对于由

N

$N$

个基本攻击操作组成的攻击策略，攻击操作搜索形成了

∣

||A||^N

$∣ ∣ A ∣ ∣^{N}$

个可能性的问题空间。此外，每个操作还与它们的幅度和步长相关联。我们将

\epsilon

$ϵ$

和

t

$t$

的大小范围离散为8个值（均匀间距），这样就可以将复合对抗攻击搜索简化为一个离散优化问题。最后，整个搜索空间的总大小为

∗

∣

)

(8*8*||A||^N)

$(8 * 8 * ∣ ∣ A ∣ ∣^{N})$

。

本文研究了三类策略空间，即构建了

∞

S_{l_∞},S_{l_2}

$S_{l_{\infty}}, S_{l_{2}}$

和

S_{unrestricted}

$S_{u n r e s t r i c t e d}$

。我们分别空间

∞

S_{l_∞},S_{l_2}

$S_{l_{\infty}}, S_{l_{2}}$

实施六个

∞

l_∞

$l_{\infty}$

-攻击者和六个

l_2

$l_{2}$

-攻击者。在不受限制的情况下，我们使用了更大的搜索空间和19个实现的攻击算法。另外，所有的

∞

S_{l_∞},S_{l_2}

$S_{l_{\infty}}, S_{l_{2}}$

和

S_{unrestricted}

$S_{u n r e s t r i c t e d}$

也采用身份攻击来表示身份操作。图4示出了每个搜索空间中的攻击策略的输出可视化。

在这里插入图片描述

Search Strategy（搜索策略）

搜索策略在寻找最佳攻击策略中起着重要的作用。在我们的问题设置中，搜索空间的规模相对较小。而且策略评估的成本比NAS等其他任务要低得多。这允许我们使用一些高性能的搜索算法。我们比较了三种广泛使用的方法，即贝叶斯优化（Snoek、Larochelle和Adams 2012）、强化学习（Zoph和Le 2016）和NSGA-II遗传算法（Deb等人，2002）。详细的实现和比较见附录B。虽然贝叶斯优化和强化学习在AutoML领域被广泛认为是有效的，但是在这个问题中，我们发现它们更耗时，收敛速度也更慢。相比之下，NSGA-II更快，因为在搜索期间不需要额外的模型优化过程。它只需要对种群更新进行几次迭代就可以快速找到最优解。

在这里插入图片描述

详细地说，NSGA-II需要维护所有可能的策略的有限集和将每个策略

∈

s ∈ S

$s \in S$

映射到实数R集的策略评估函数。在这项工作中，我们使用公式3作为政策评估函数。NSGA-II算法分三步探索潜在攻击策略的空间，即种群初始化步骤，生成具有随机策略的种群

P_0

$P_{0}$

；探索步骤，包括攻击策略的交叉和变异，最后是一个开发步骤，利用存储在整个评估策略历史中的隐藏有用知识，找到最优策略。整个过程如Alg1所示。在本文的剩余工作中，我们采用了NSGA-II算法进行策略搜索。

4、Experiments

Experiment Setup

为了验证CAA的性能，在11个开源防御模型上对

∞

S_{l_∞},S_{l_2}

$S_{l_{\infty}}, S_{l_{2}}$

和

S_{unrestricted}

$S_{u n r e s t r i c t e d}$

的搜索攻击策略进行了评估。我们在CIFAR-10（Krizhevsky，Hinton等人，2009）和ImageNet（Deng等人，2009）数据集上进行了

∞

l_∞

$l_{\infty}$

和

l_2

$l_{2}$

攻击实验。我们对Bird&Bicycle（Brown et al.2018）数据集执行无限制攻击。稳健的准确度被记录为测量，以与最近10名顶级攻击者进行比较。在执行过程中，我们将政策的所有中间结果与（Croce和Hein 2020）相似地进行整合。

Details of Search Space

（搜索空间的详细信息）CAA的候选池由32个攻击操作组成，即6个

∞

l_∞

$l_{\infty}$

-攻击、6次

l_2

$l_{2}$

攻击、19次无限制攻击和最后一次身份攻击（即身份操作）。已实现的攻击算法的详细摘要如表1所示。1.我们借用了开源攻击工具箱中的一些算法的代码，比如Foolbox（Rauber，Brendel，Bethge 2017）和Advertorch（Ding，Wang，Jin 2019）。每个基本攻击者的实现和引用可在附录A中找到。

在这里插入图片描述

Data configuration

（数据配置）对于CIFAR-10，我们在一个小的子集上搜索最佳策略，该子集包含从序列集中随机选择的4000个样本。测试集中总共有10000个样本用于评估搜索到的策略。对于ImageNet，由于整个验证集比较大，我们分别从训练和测试数据库中随机选取1000张图像进行策略搜索和1000张图像进行评估。对于Bird&Bicycle，我们使用所有250个测试图像进行评估，并随机选择1000个训练图像进行攻击策略搜索。

Summary of Experiments

（实验摘要）我们调查了四种情况：1）最佳攻击，在候选池中搜索最佳单个攻击者；2）诱捕攻击，搜索多个攻击者的合谋；3）

CAA_{dic}

$C A A_{d i c}$

，直接搜索给定数据集上的CAA策略；4）

CAA_{sub}

$C A A_{s u b}$

，通过攻击对抗性训练CIFAR10模型作为替代进行搜索，并转移到其他模型或任务中。为了公平起见，我们将我们的方法与之前最先进的攻击者在11个收集的防御模型上进行了比较：Advtrain（Madry et al.2017）、TRADES（Zhang et al.2019）、AdvPT（Hendrycks、Lee和Mazeika 2019）、MMA（Ding et al.2019）、JEM（Grathwohl et al.2019）、PCL（Mustafa et al.2019）、Semi Adv（Carmon et al.2019）、FD（Xie et al.2019），AdvFree（Shafahi等人，2019年），贸易24和LLR5。接下来，我们利用多种体系结构（VGG16（Simonyan 2014）、ResNet50（He et al.2016）、Inception（Szegedy et al.2015）和数据集（MNIST（LeCun et al.1998）、CIFAR-100、SVHN（Netzer et al.））来研究CAA在黑盒和白盒设置下的可转移性。最后，研究了不同策略搜索算法和攻击策略长度N的影响。分析了非目标攻击和目标攻击搜索策略的区别。在这些烧蚀实验中可以发现一些见解。

Comparison with State-of-the-Art

（与最新技术的比较）表2表示

∞

l_∞

$l_{\infty}$

-基于四种变体的攻击结果，即：

CAA_{sub}

$C A A_{s u b}$

、

CAA_{dic}

$C A A_{d i c}$

、EnsAttack和BestAttack对CIFAR-10的攻击数据集。大多数的研究工作都是在这种情况下研究模型的稳健性，因此我们可以收集更多的防御来进行评估。比较的攻击者是150步ODI-PGD（10步ODI和20次重启），100步PGD和APGD（10次重启），FAB和AA。FAB和AA的超参数与原论文（Croce和Hein 2020）一致。所有这些攻击者的梯度评估总数（复杂度）都大于1000。相比之下，我们的CAAsub具有较低的复杂度（800），并且以较高的错误率破坏了模型。这意味着即使是替换攻击策略也可能具有较高的时间效率和可靠性。直接搜索感兴趣的任务可以进一步提高性能。从表的最后一行可以看出，

CAA_{dic}

$C A A_{d i c}$

建立了更强的攻击策略，鲁棒精度平均下降了0.1%。除了CAA之外，我们还评估了图2中的两个可选方案：BestAttack和EnsAttack。BestAttack的最终搜索策略是MT LinfAttack，在

∞

S_{l_∞}

$S_{l_{\infty}}$

条件它是中最强的攻击者。然而，结果表明，最好的单个攻击者在现有方法面前并不具有竞争力。EnsAttack搜索包含MT-Linf、PGD-Linf和CW-Linf攻击的策略。与BestAttack相比，EnsAttack融合了多个攻击，取得了更好的效果。但这仍然比民航局的政策更糟糕。这意味着CAA在经验上比攻击者的集合更好。对于CIFAR-10上基于

l_2

$l_{2}$

的攻击，我们的方法也有很好的性能。

在这里插入图片描述

ImageNet上的结果显示在表3。我们证明了这一点与CIFAR-10相比，CAA在ImageNet上获得了更大的改进，尤其是

CAA_{sub}

$C A A_{s u b}$

在攻击

∞

l_∞

$l_{\infty}$

对抗训练模型时，准确率达到了38.30%，比最先进的模型提高了2%左右。这意味着CAA更适合攻击复杂的分类任务。ImageNet分类有更多的分类和更大的图像输入大小。此外，我们还发现，在ImageNet上，由基础攻击者生成的对抗性示例更加多样化。对于这样一个复杂的任务，攻击策略的设计有更大的空间。

在这里插入图片描述

对于无限制攻击，我们选择了在无限制对抗示例竞赛（Brown et al.2018）中提出的Bird&Bicycle基准。排名前两位的防御模型LLR和TRADESv2用于评估。为了公平起见，我们只使用竞赛中的热身攻击作为搜索空间

S_{unrestricted,}

$S_{u n r e s t r i c t e d,}$

，避免了防御模型从未见过的攻击。LLR和TRADESv2对腐败、空间攻击和SPSA攻击的鲁棒准确率接近100%。但在CAA合成这些攻击后，LLR和TRADESv2的鲁棒精度迅速下降到零左右。结果表明，现有的无限制对抗防御模型对单个测试攻击者的适应性严重过强。在不受限制的攻击环境中，我们无法很好地防御CAA。因此，我们认为要实现真正的无限制对抗健壮性，还有很多工作要做。

Analysis of searched policy

（搜索策略分析）我们将搜索到的关于

∞

S_{l_∞},S_{l_2}

$S_{l_{\infty}}, S_{l_{2}}$

和

S_{unrestricted}

$S_{u n r e s t r i c t e d}$

的最佳策略可视化到Tab2。在CIFAR-10分类任务中，通过攻击敌方训练模型来搜索策略。在所有

∞

l_∞

$l_{\infty}$

和

l_2

$l_{2}$

和无限制攻击场景中，CAA都倾向于选择强攻击。以

∞

S_{l_∞}

$S_{l_{\infty}}$

策略为例，CAA选择最强的MT-LinfAttack作为第一和第二位置攻击，放弃较弱的攻击者，如一步FGSM。因此，我们认为一个良好的候选攻击池对CAA的性能至关重要。另一个基础是CAA喜欢一些不同的基础攻击者组合的策略。这意味着由MI-Linf和PGD-Linf攻击形成的策略通常不会有什么改进，因为它们之间的差别很小（原理和目标函数相同）。相比之下，在

∞

S_{l_∞}

$S_{l_{\infty}}$

的最佳策略中，CAA选择了更为多样化的基于边缘丢失的CW-Linf攻击来辅助基于交叉熵丢失的攻击者，从而提高了攻击性能。

Attack transferability

（攻击可转让性）我们研究了CAA在两种情况下的可转移性：1）黑盒设置和2）白盒设置。在黑盒设置下，我们无法得到目标模型的梯度。相反，我们使用CAA搜索替代模型上的策略，并生成对抗样本来攻击目标模型。在白盒设置中，允许梯度评估，因此在替代任务或模型上搜索的策略用于直接在目标模型上生成对抗性样本。

Black-box Transferability of CAA

（CAA的黑盒可转移性）这里我们讨论CAA是否可以用于搜索黑盒转移攻击。为了满足这一要求，我们对原来的CAA做了一些修改。具体来说，在对抗性样本生成阶段，我们使用攻击策略s来攻击替代模型。然后在目标模型上对这些对抗样本进行了测试。以目标模型的鲁棒精度作为策略的评价分数。除此之外，整个搜索过程保持不变。我们把这个变体命名为

CAA_{trans}

$C A A_{t r a n s}$

。在攻击可转移性实验中，我们使用了三种不同体系结构的模型（VGG16、Inceptionv3和ResNet50），并通过标准对抗训练进行防御。结果记录在Tab中4.第一列显示实验设置。例如，R→V意味着我们使用ResNet50作为替代模型来攻击VGG16。

在这里插入图片描述

结果表明，在大多数转移攻击环境下，CAA都能获得更好的性能。特别是采用VGG16作为替代模型时，攻击强度明显提高，目标模型精度下降3%。结果表明，自动搜索过程也有助于发现更黑盒可转移的攻击策略，而不限于白盒情况。通过对附录D中搜索到的可转移策略的可视化，我们发现

CAA_{trans}

$C A A_{t r a n s}$

没有采用某些“强”攻击，因为此类攻击可能具有较差的可转移性。相反，策略中选择了FGSM或MI-Linf攻击作为更好的可转移组件，这解释了

CAA_{trans}

$C A A_{t r a n s}$

可以提高攻击可转移性的原因。

White-box Transferability of CAA

（CAA的白盒可转移性）在这里，我们试图了解是否有可能在白盒情况下转移攻击策略，即在替代任务或模型上搜索的策略用于攻击目标模型。详细的实验见附录C。从结果来看，我们强调CIFAR-10上搜索到的策略仍然可以很好地转移到许多模型体系结构和数据集。因此，我们相信CAA不会“过度适应”数据集或模型体系结构，它确实找到了抓住真正弱点的有效策略，并且可以应用于所有此类问题。但是，不能保证攻击策略在防御系统之间传输。提高防御系统间可转移性的一个经验做法是在候选池中使用更强、更多样化的攻击算法。引用位于表2。通过在

∞

S_{l_∞}

$S_{l_{\infty}}$

中使用6个强攻击者，

CAA_{sub}

$C A A_{s u b}$

在多种防御模型上都取得了令人满意的效果。

5、Ablations

Analysis of the policy length N

（策略长度N的分析）我们进行了一系列的实验，以探讨一个较长的策略是否具有更强的攻击能力，该策略可以采用更多、多样的基攻击者。我们选择了长度为1、2、3、5和7的五个策略。图5显示了鲁棒精度随策略长度的曲线。当N=1时，CAA等于在候选池中找到最佳的基攻击者，因此在这种情况下性能最差。随着N的增加，攻击策略在所有

∞

l_∞

$l_{\infty}$

、

l_2

$l_{2}$

和无限制设置下都变得更强。我们发现策略长度对

l_2

$l_{2}$

攻击设置的影响最小。基本攻击越多，二级攻击的优化步骤就越多，这是合理的。相比之下，N对无限制攻击的性能影响很大。当使用大于3的搜索攻击策略时，在不受限制的设置下，准确率迅速下降到零左右。

在这里插入图片描述

Different Search Methods

（不同的搜索方法）表5介绍了随机搜索、贝叶斯优化、强化学习和NSGA-II遗传算法四种优化方法的性能和搜索时间。每种方法的详细实现见附录B。随机搜索是以100个随机策略进行试验并选出最佳策略作为基线。与基线相比，所有启发式算法都能找到更好的策略。虽然贝叶斯优化和强化学习在大空间搜索中被广泛认为是有效的，但是在这个问题中，我们发现它们更耗时，更容易陷入局部最优。相比之下，NSGA-II以3gpu/d的低成本找到更好的策略，并获得更好的性能。

在这里插入图片描述

Target vs. Non-target attack

（目标与非目标攻击）目标攻击是一种特殊的应用场景，攻击者通过欺骗模型来输出他们想要的目标标签。否则，没有给出目标标签就称为非目标攻击。我们在附录C中的目标攻击设置下对CAA进行了实验。对于目标攻击，CAA搜索随机初始化较少的策略。这表明没有随机初始化的攻击者更适合目标设置。此外，与边际损失相比，交叉熵损失的基攻击者更受CAA的青睐。CAA搜索的策略在目标攻击方面也得到了改进。

6、Conclusion

我们提出了一个自动学习攻击策略的过程，该过程是由一系列基本攻击者组成的，用于破坏ML系统。通过将我们的搜索策略与10个最近的攻击者在11种不同防御方式下的搜索策略进行比较，表明我们的方法在较短的运行时间内获得了较好的攻击成功率。经验证明，搜索更好的算法和超参数也有助于对抗性攻击。

我们认为我们工作的最重要的扩展是如何防御能够自动搜索最强攻击算法的攻击者。从这个角度出发，我们将在今后的工作中研究基于CAA的对抗性训练方法

原文链接：https://blog.csdn.net/weixin_43682519/article/details/118569717

复合对抗攻击

1、 Abstract

2、Introduction

3、Preliminaries and Related work（准备工作和相关工作）

Adversarial Attack

Automated Machine Learning

Composite Adversarial Attacks（复合对抗攻击）

Problem formulation（问题描述）

Constraining lp-Norm by Re-projection（重投影约束lp范数）

Search Objective（搜索目标）

Search Space（搜索空间）

Search Strategy（搜索策略）

4、Experiments

Experiment Setup

5、Ablations

6、Conclusion

你可能也喜欢