贪心算法 之 哈夫曼编码
1.最优二叉树:(哈夫曼树)
1>结点的权:赋予叶子结点以个有意义的值;
2>结点的路径长度:从根结点到当前结点的的长度
结点的带权路径长度:W*L (W:权 L:路径长度)
3>二叉树的带权路径长度:一颗二叉树的所有叶子结点的带权路径长度之和
4>最优二叉树:一颗二叉树的带权路径最小,就是最优二叉树
2.哈夫曼树的特点:
1>没有单分支;
2>当叶子为n时,双亲为n-1;
构造一颗哈夫曼树:
(1)根据给定的n个权值{w1, w2,…,wn},构成n棵二叉树的集合F= {T1, T2,…,Tn},其中每棵二叉树Ti中只有一个带权为wi的根节点,其左右子树均空。
在F中选取两棵权值最小的二叉树作为左、右子树构造一棵新的二叉树,置新 构造二叉树的根节点的权值为其左、右子树根节点的权值之和。
从F中删除这两棵树,同时将新得到的二叉树加入到F中。
重复(2)、(3),直到F中只含一棵树时为止。这棵树便是最优二叉树(哈夫曼树)。 从以上叙述可知,哈夫曼树中权值最小的两个节点互为兄弟节点。
例子:
设有一英文文章,共有A,B,C,D四种字符,它们的出现频率依次为F{9,3,6,4},
算法一:链式哈夫曼树
思想:
1>从森林{9,3,6,4}中选取最小和次小的两颗二叉树构成一颗新的二叉树,并放回森林。(左子女最小,右子女次小)
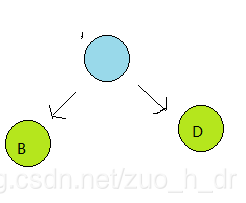
2>重复第一步,直到森林中只剩一颗二叉树;
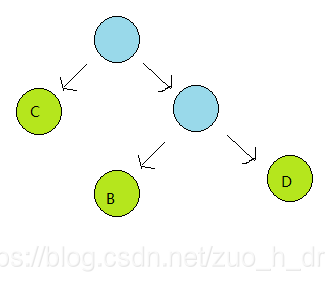
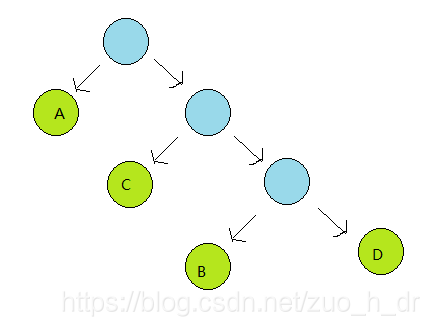
算法描述:实现链式哈夫曼树:
数据结构:结点:

typedef struct node{
char word;
int weight;
struct node *left,*right;
}HufNode;
森林:
有N个叶子结点的初始森林(数组)

1>定义森林:
HufNode **F;
F=(HufNode**)malloc(n*sizeof(HufNode*));2>初始化森林:
HufNode *p;
char a[]={A,B,C,D};
int b[]={9,3,6,4};
for(int i=0;i<n;i++){
p=(HufNode*)malloc(sizeof(HufNode));
p->word=a[i];
p->right=p->left=^;
F[i]=p;
}实现最优二叉树:
for(int loop=1;loop<n;loop++){ //找n-1次最小次小
复习:找最小次小;
min=0;
minx=1;
for(int i=1;i<n;i++){
if(a[i]<a[min]){
minx=min;
min=i;
}
else if(a[i]<a[minx])
minx=i;
}
}实践 1 //第一种 找最小次小,解决重复值,含^的情况
for(int i=1;i<n;i++){
int min,minx,t; //最小,次小
for(min=0;min<n&&(!F[min]);min++); //找到第一个非空元素
for(minx=min+1;minx<n&&(!F[min]);minx++); //找到第二个非空元素
for(t=minx;t<n;t++){ //找最小次小
if(F[t]){
if(F[t]->weight<F[min]->weight){
minx=min;
min=t;
}
else if(F[t]->weight<F[minx]->weight){
minx=t;
}
}
} 生成二叉树;
p=(HufNode*)malloc(sizeof(HufNode)); //生成双亲结点
p->word=‘x’;
p->weight=F[min]->weight+F[minx]->weight;
p->left=F[min]; //最小
p->right=F[minx]; //次小
F[min]=p; //放回数组
F[minx]=^;
}
哈夫曼树的输出:
算法二:以数组实现哈夫曼树
1.存储:
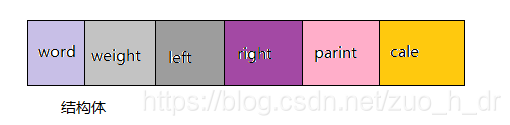
typedef struct{
char word;
int weight;
int left,right,parent;
int *cale //编码
}Huff;
实现结构体数组:
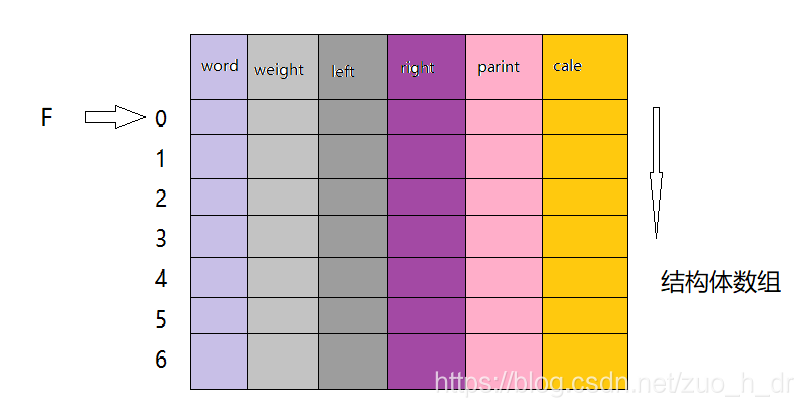
6=2*4-1
Huff *F;
F=(Huff*)malloc((2*n-1)sizeof(Huff));
//初始化
for(int i=4;i<n;i++){
printf("请输入:");
scanf("%c",&ch);
F[i].word=ch;
scanf("%d",&we);
F[i].weight=we;
}
//建立关系:
int i,min,minx;
for(int loop=0;loop<n-1;loop++){
for(min=0;min<n+loop&&F[min].parint!=-1;min++);
for(minx=0;i<minx+loop&&F[minx].parint!=-1;minx++);
for(i=0;i<n+loop;i++){
}
}
编码:
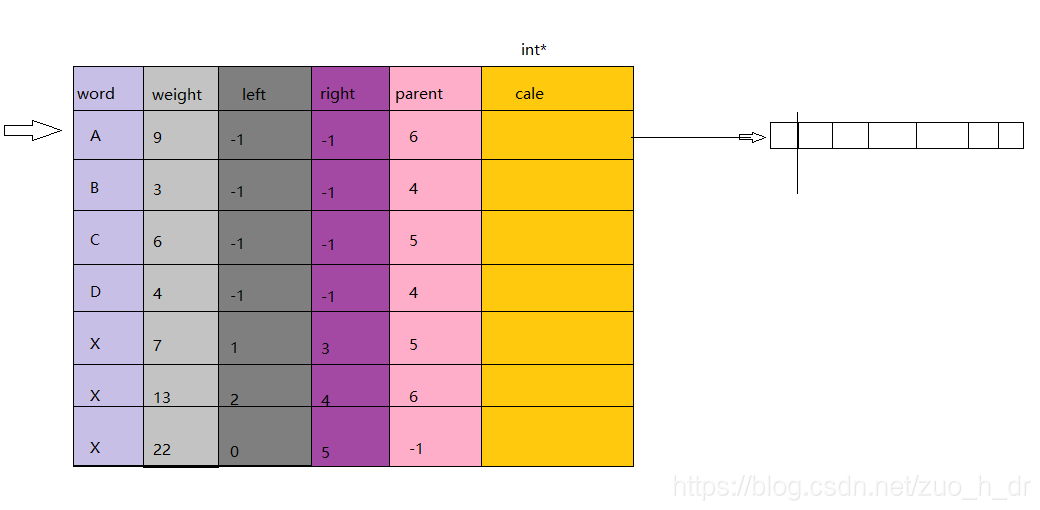
例:给B编码,找到B的双亲结点,判断B是双亲的左子女还是右子女,来编码一位,再查找双亲的双亲,循环执行,直到找到根结点为止。
存储结构:
用一个n-1的int数组来存放编码,下标为0的空间存放编码长度(岗哨),从下标1开始正式存放编码。
C语言描述:
//哈夫曼编码 数组实现
#include <stdio.h>
#include <stdlib.h>
typedef struct node{
char word; //字符
int weight; //字符的权
int left; //左子女的下标
int right; //右子女的下标
int parint; //双亲结点的下标
int *code; //编码数组的首地址
}Huffnode;
void CreatHuffmanTree(Huffnode *F,int n); //函数声明
void CreatHuffmancode(Huffnode *F,int n);
void PrintHuffmancode(Huffnode *F,int n);
int main (void){
Huffnode *F;
int n,w[4]={9,3,6,4};
char ch[4]={'A','B','C','D'};
printf("请输入:");
scanf("%d",&n);
//创建森林
F=(Huffnode*)malloc((2*n-1)*sizeof(Huffnode));
for(int i=0;i<n;i++){
F[i].word=ch[i];
F[i].weight=w[i];
F[i].left=F[i].right=F[i].parint=-1;
}
//创建哈夫曼树
CreatHuffmanTree(F,n);
//创建 哈夫曼编码
CreatHuffmancode(F,n);
//输出
PrintHuffmancode(F,n);
free(F);
}
void CreatHuffmanTree(Huffnode *F,int n){ //创建哈夫曼树
int loop=0;
int k1,k2;//最小次小
for(loop=0;loop<n-1;loop++){
for(k1=0;k1<n+loop&&F[k1].parint!=-1;k1++); //找到第一个元素
for(k2=k1+1;k2<n+loop&&F[k2].parint!=-1;k2++); //找到第二个元素
for(int i=k2;i<loop+n;i++){ //找到最小,次小
if(F[i].parint==-1){
if(F[i].weight<F[k1].weight){
k2=k1;
k1=i;
}
else if(F[i].weight<F[k2].weight){
k2=i;
}
}
}
F[n+loop].weight=F[k1].weight+F[k2].weight;
F[n+loop].left=k1; //最小在左子女
F[n+loop].right=k2; //次小在右子女
F[n+loop].parint=-1;
F[n+loop].word='X';
F[k1].parint=F[k2].parint=n+loop;
}
}
void CreatHuffmancode(Huffnode *F,int n){ //创建哈夫曼编码
int c,pa;
int *p;
for(int i=0;i<n;i++){
F[i].code=p=(int*)malloc(n*sizeof(int));
p[0]=0; //p[0]用来充当岗哨
c=i;
while(F[c].parint!=-1){ //当找到根结点时终止循环
pa=F[c].parint;
if(c==F[pa].left){
p[++p[0]]=0;
}
else{
p[++p[0]]=1;
}
c=pa; //再找双亲的双亲
}
}
}
void PrintHuffmancode(Huffnode *F,int n){
for(int j=0;j<n;j++){
printf("%c的编码是:",F[j].word);
for(int i=F[j].code[0];i>0;i--){ //由子女找双亲,编的码,故倒着输出
printf("%d",F[j].code[i]);
}
printf("\n");
}
}