转自:
http://www.cnblogs.com/fornever/archive/2011/11/15/2249492.html
写的有点儿俗,理论性不是很强,不过还算通俗易懂。总之,谢谢上位大侠的解释~~~
平衡二叉树定义(AVL):它或者是一颗空树,或者具有每以下性质的二叉树:它的左子树和右子树的深度之差的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
平衡因子(bf):结点的左子树的深度减去右子树的深度,那么显然-1<=bf<=1;
很显然,平衡二叉树是在二叉排序树(BST)上引入的,就是为了解决二叉排序树的不平衡性导致时间复杂度大大下降,那么AVL就保持住了(BST)的最好时间复杂度O(logn),所以每次的插入和删除都要确保二叉树的平衡,那么怎么保持平衡呢?
我努力看了看数据结构上的讲解,但是看的只晕+_+!我对他的讲解很无语,他所谓的“旋转”操作讲的不明不白,看的我气的蛋疼!你说你旋转,你得说清是如何旋转?以那个结点为中心,那些或者说那个结点转了,那些结点不动。你就在哪里旋转来旋转去的,谁知道你是咋转的,你在哪慢慢转吧!哥转不过你,另找高明!于是在网上找啊找,只为想搞明白是到底怎么转的!
点击打开链接
让我对“旋转”有所领悟,表示感谢!
插入时:
那究竟是如何“转”的呢?
首先必须明白一个核心操作,不让它叫“旋转”!而叫——>“两个结点的变换”
如图:

就拿第一个来说->点100和101的变换:
点101占据点100的位置,点100换到了101的对面的位置,其他点的相对位置不变。
我们可以更直观的理解为:把101结点“上提”一下!
分析:101>100,所以100可以作为101的左孩子;
也就是在二叉排序树中,两个结点这样的变换操作是可行的,是符合二叉排序树的性质。
不仅这个简单的图,任何复杂的二叉排序树都可以,你可以试试,也许你会说如果点101左边有孩子怎么办?别着急~,当然有办法!
下边正式说这个图的四种不平衡情况(插入时)及操作:
首先还需要明白一个概念->最小不平衡子树的根结点:也就是当你进行插入操作时,找到该需要插入结点的位置并插入后,从该结点起向上寻找(回溯),第一个不平衡的结点即平衡因子bf变为-2或2。
为什么要引入这个最小不平衡根结点的概念,因为在插入时,对该子树进行保持平衡操作后,其它的结点的平衡因子不会变,也就是整棵树又恢复平衡了。为什么呢?
你想想不平衡点的bf一定是-2或2吧,经过平衡操作后,他会把一边子树的一个结点分给另一边的子树,也就是一边的深度分给另一边,这样就平衡了!
比如,插入前:左边是深度1,右边深度是0;插入后左边深度是2,右边深度是0,经过平衡后左边深度是1,右边深度是1;
那么你说插入前和插入后该根结点所领导的子树的深度变没??仍是1,显然没变!那么就仍保持了这棵树的平衡了!
下面即四种情况分别为:左左、右右、左右、右左,每种情况又有两个图:①、②,①是该情况的最简单的图形,②是该情况的一般的图形;
设x为最小不平衡子树的根结点,y为刚插入的点
左左:
即在x的左孩子a的左孩子c上插入一个结点y(该结点也可以是c,如图①),即y可以是c,也可以是c的左孩子(如图②),也可以是c的右孩子(不在画出)

图①就不用说了,结点x和结点a变换,则树平衡了;那么图②就是树中的一般情况了a结点有右孩子d,那要进行x和a变换,那么a的右孩子放哪啊?
很简单,如图放在x的左孩子上;分析:x>d,d>a,所以d可作为x的左孩子,且可作为a的右孩子中的孩子。下边这样的类似情况不再一一分析,自己分析分析~
实现:找到根结点x,与它的左孩子a进行交换即可使二叉树树再次平衡;
右右:
即在x的右孩子a的右孩子c上插入一个结点y(该结点也可以是c,如图①),即y可以是c,也可以是c的右孩子(如图②),也可以是c的左孩子(不在画出)
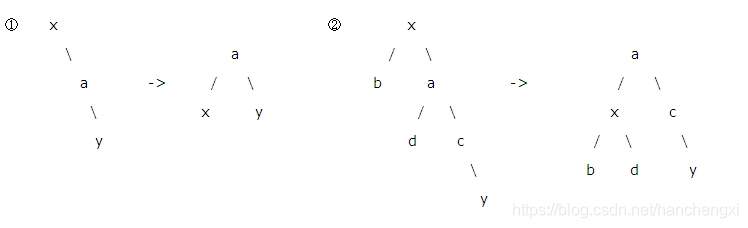
实现:找到根结点x,与它的右孩子a进行交换即可使二叉树树再次平衡;
左右:
即在x的左孩子a的右孩子c上插入一个结点y(该结点也可以是c,如图①),即y可以是c,也可以是c的右孩子(如图②),也可以是c的左孩子(不在画出)
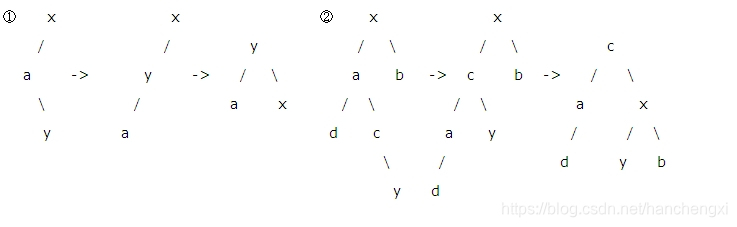
这个左右和下边的右左,稍微复杂了点,需要进行两次交换,才能达到平衡,注意这时y是c的右孩子,最终y作为x的左孩子;若y是c的左孩子,最终y作为a
的右孩子,画图分析一下~~下边类似,不再敖述。
实现:找到根结点x,让x的左孩子a与x的左孩子a的右孩子c进行交换,然后再让x与x此时的左孩子c进行交换,最终达到平衡;
右左:
即在x的右孩子a的左孩子c上插入一个结点y(该结点也可以是c,如图①),即y可以是c,也可以是c的右孩子(如图②),也可以是c的左孩子(不在画出)
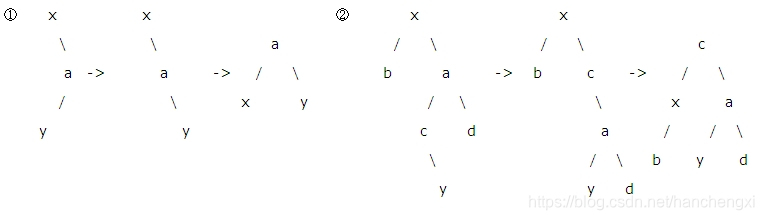
实现:找到根结点x,让x的右孩子a与x的右孩子a的左孩子c进行交换,然后再让x与x此时的右孩子c进行交换,最终达到平衡;
上边的四种情况包含了所有插入时导致不平衡的情况,上面给出的仅仅是一棵大树中的最小不平衡子树,一定要想清楚,别迷了!
另外一定要注意这个交换操作,比如a与b交换(a在上,b在下),b一定要占据a的位置!什么意思?就是b要放在(覆盖)储存a的那块内存上,
再通俗点说,若a是x的左孩子,则交换后b要做x的左孩子;这就是所谓的b占据a的位置!
那么如何找到最小不平衡子树的根结点x,并判断出它是属于那种情况的?
插入一个结点时,我们首先找到需要插入的位置,并插入;数据结构上用的是递归,不要说递归太浪费时空,你想想一个含2^31个结点的平衡二叉树的深度大约是31吧,它递归再多也不就是31层!而且递归代码短小、精悍、富含艺术之美!所以我认为对于这个平衡二叉树,用递归很合适!
显然插入之后就要检查是否出现不平衡的结点,那么如何检查?
我们知道,你插入的时候用的是递归,一条线找到要插的位置,并插入;那么谁的平衡因子的有可能变呢?
不难想象,只有该条线上的结点的平衡因子有可能改变!那么我们在回溯的时候不就可以找到第一个不平衡的子树的结点?!
可是我们如何判断该结点的平衡因子是否应该改变,显然要看它被插入结点的一边的深度是否增加;
如何看它被插入结点的一边的深度是否增加?
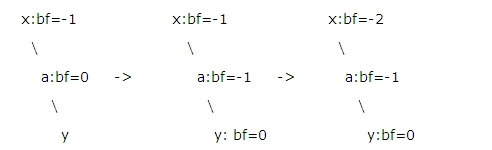
如上图,如何看x的右孩子a(即被插入结点的一边)的深度增加?我们知道在a的右孩子上插入了结点y那么a的bf是一定要减1
那么x结点的bf?可根据a的bf决定是否改变!
若a:bf=-1或1,那么a之前一定为0,表示a的深度增加了,那么x的bf可根据a是x哪一边的孩子决定+1或-1;
若a:bf=0,那么a之前一定为-1或1,表示a的深度没增加,那么不仅x的bf就不用变,该条线上的所有结点的bf都不用变,直接返回即可;
当然了,那么找到最小不平衡子树的根结点x了,如何判断它属于哪种不平衡呢?
①根据上边的几种情况,我们需要知道两个方向,在回溯时可以记录一下该结点到下一个结点的方向0:左、1:右为第二个方向,传递给上一层中,那么上层中的方向就是一个方向,有了这两个方向就能确定是哪种不平衡了。
还就上边的图说吧~可以定义一个全局变量secdirection(第二个方向),也可在递归中定义一个局部变量,返回给上一层。在回溯到a中时,secdirection=1,到x的时候
x->a的方向也为1,定义firdirection=1;而这时x:bf=-2;那么就找到了最小不平衡子树的根结点x,又知道了两个方向,那么进行相应的平衡操作不就行了。
②其实我代码中的就是按照①写的,可是刚又想了,其实不用用个变量记录第二个方向,可以根据a的bf确定它的第二个方向,a:bf=-1说明右孩子的深度增加,y加到右孩子上;
a:bf=1;说明左孩子的深度增加,y加到左孩子上;
好了,找到了最小不平衡子树的根结点x了,也知道了那种不平衡,调用keepbalance(…)就使树平衡了,可是某些结点的平衡因子在变换是变了~~咋办?
我就是一种一种情况推出来的,不知道别人怎么变的,每一种情况都有固定的几个点变了,变成了一个固定的值!谁有更好的办法,请多多指教!
下边一一列出(插入操作中)变换后bf改变的结点及值:
左左:前a->bf=1 后 x->bf=0,a->bf=0;右右:前a->bf=-1 后x->bf=0,a->bf=0;显然左左与右右的x与a变换后的bf都为0;
左右、右左中结点bf的改变要根据之前c的bf!
左右:若c->bf=1,则x->bf=-1,a->bf=0,c->bf=0;若c->bf=-1,则x->bf=0,a->bf=1,c->bf=0;若c->bf=0,则x->bf=0,a->bf=0,c->bf=0;
右左:若c->bf=1,则x->bf=0,a->bf=-1,c->bf=0;若c->bf=-1,则x->bf=1,a->bf=0,c->bf=0;若c->bf=0,则x->bf=0,a->bf=0,c->bf=0;
可以发现,当左右、右左的c->bf相同时x与a的bf刚好取相反的值。
好了,到现在插入一个结点的二叉树终于平衡了,相应的平衡因子也修改了!插入算是完成了!!
删除时:
删除类似插入的操作,蛋又不同,删除会有一些特殊情况需要特殊处理,当然核心操作“保持平衡”是不变的!
删除时少一个结点,也就是该结点所在的子树深度可能会减小,而插入时多一个结点,该结点所在的子树深度可能会增加,
所以递归删除一个结点时,回溯时找到最小不平衡子树的根结点时,要向相反的方向去找属于哪种情况;
如图:
y为要删除的结点;
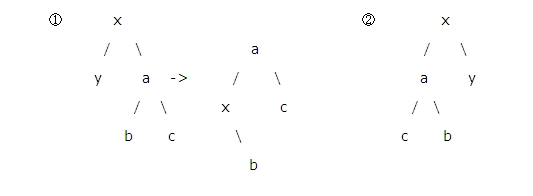
图①:y结点删除后,回溯到x结点x:bf=-1变为x:bf=-2;则需从相反方向即从x的右孩子的方向向下检查属于哪种情况,显然第一个方向为1:右;
第二个方向看a:bf的值——若为1时,那就相当于插入时‘右左’的情况;若为-1时,那就相当于插入时‘左左’的情况;可现在a:bf既不是1也不是-1
而是0,这就是删除的特殊情况了!我们不妨试试对他进行类似于插入时的‘右右’操作,看怎么样~ 如上图,经过变换后该子树平衡了!但是因子的
修改就跟插入时的‘右右’不一样了!此时变为:x:bf=-1,a:bf=1;所以我们不妨就把a:bf=0也归纳为删除的‘右右’或‘左左’(如图②,不再敖述)操作;
那么删除时因子的改变需在插入时因子的改变中添加上:
左左:前a:bf=0 后x:bf=1,a:bf=-1; 右右:前a:bf=0 后x:bf=-1,a:bf=1;其他不变!
插入时结束结点平衡因子的修改,直接返回(也就是该树已经平衡了):
回溯时发现儿子结点的平衡因子为0(当发现不平衡结点,并进行平衡操作后,平衡后根结点的bf一定为0,也结束了)
但是删除时结束结点平衡因子的修改,直接返回,就与插入时不一样了:回溯时发现儿子结点的平衡因子为-1或1!
再删除操作中,平衡一个子树后,该子树的深度不一定不变,而只有上边那种特殊情况该子树的深度不变,其他都会变!
可以想象,其实是很简单的道理:除了特殊情况其他都与插入的情况一模一样,说白了就是把深度大的子树(根结点的其中一个)向深度小子树贡献一个深度,
那么这样一来,该子树(对于根结点所领导的树)的深度是不是比原来的小1了?!所以要继续向上一个一个进行检索,直到根结点为止!
好了,到这里删除也算是说完了,可以贴代码了吧~
平衡二叉树的C实现:
View Code
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef int Elemtype;
typedef struct Balanced_Binary_Tree
{
Elemtype e;
int bf;
struct Balanced_Binary_Tree *child[2];
}*AVL;
///------------简单的位操作-------------------
void setbit(char *i,char val,char pos)
{
if(pos==1)
(*i)=(*i)|1;
else
{
if(val==1) (*i)=(*i)|2;
else (*i)=(*i)&1;
}
}
char getbit(char i,char pos)
{
///调试时,发现这里能返回2///
// return (i&pos); 出错的地方
return (i&pos)&&1;
/
}
///--------------------------------------------
///-----------生成一个结点---------------------
AVL createnode(Elemtype e)
{
AVL node=NULL;
node=(AVL)malloc(sizeof(struct Balanced_Binary_Tree));
node->e=e; node->bf=0;
node->child[0]=node->child[1]=NULL;
return node;
}
///---------------------------------------------
///★★★★★★★★AVL的核心操作★★★★★★★★★★★★
///★★★★★★★★★保持平衡★★★★★★★★★★★★★★
//改变因子函数
void setfactor(AVL f,int button)
{
char fir=button/10,sec=button%10;
AVL s=f->child[fir],ss=s->child[sec];
char choice=ss->bf;
int a=1,b=0;
//调试时发现,删除时的特殊情况/
/插入时,不会有这种情况,若button=0,则s->bf=1//
/若button=11,则s->bf=-1;然而删除时,却会出现/
/button=0或者button=11时 s->bf=0!!!!!!!
/那么这种特殊情况,平衡后所得的因子就跟一般的//
/不一样了!!!如下///
if(button==0 && s->bf==0) f->bf=1,s->bf=-1;
else if(button==11 && s->bf==0) f->bf=-1,s->bf=1;
///
else if(button==0 || button==11)
{
f->bf=0;
s->bf=0;
}
else
{
/写博客时,发现这里有问题///
// if(button==1) choice=-choice;
/但是为什么我测试的时候怎么都对?!///
/经再次测试,上边确实错了!!!
/改为下边应该就对了吧///
if(button==1) {a^=b,b^=a,a^=b;}
if(choice==-1) f->bf=a,s->bf=b;
else if(choice==0) f->bf=s->bf=0;
else f->bf=-b,s->bf=-a;
ss->bf=0;
}
}
//两节点变换函数
void conversion(AVL *T,char direction)
{
AVL f=*T,s=f->child[direction];
f->child[direction]=s->child[!direction];
s->child[!direction]=f;
*T=s;
}
//保持平衡函数
void keepbalance(AVL *T,char fir,char sec)
{
AVL *s=&((*T)->child[fir]);
int button=fir*10+sec;
if(button==0 || button==11)
{
setfactor((*T),button);
conversion(T,fir);
}
else
{
setfactor((*T),button);
conversion(s,sec);
conversion(T,fir);
}
}
///★★★★★★★★★★★★★★★★★★★★★★★★★★
///------------插入时的选向操作-------------------
void selectforInsert(AVL *T,char *info,int direction)
{
AVL cur=*T;
char firdirection,secdirection;
if(direction==0) (cur->bf)++;
else (cur->bf)--;
if(cur->bf==0) setbit(info,1,1);
else if(cur->bf==-1 || cur->bf==1) setbit(info,direction,2);
else
{
firdirection=direction;
secdirection=getbit(*info,2);
keepbalance(T,firdirection,secdirection);
setbit(info,1,1);
}
}
//----------------------------------------------
//*************插入操作************************//
char InsertAVL(AVL *T,Elemtype e)
{ //可用于查询
char info;
if(!(*T))
{
(*T)=createnode(e);
return 0;
}
else if((*T)->e==e) return -1;
else if((*T)->e>e)//左
{
info=InsertAVL(&((*T)->child[0]),e);
if(getbit(info,1)) return info;
selectforInsert(T,&info,0);
}
else //右
{
info=InsertAVL(&((*T)->child[1]),e);
if(getbit(info,1)) return info;
selectforInsert(T,&info,1);
}
return info;
}
//*********************************************//
//-------------删除时的选向操作--------------------
void selectforDelete(AVL *T,char *info,char direction)
{
AVL cur=(*T);
char firdirection,secdirection;
if(direction==0) (cur->bf)--;
else (cur->bf)++;
if(cur->bf==0) *info=0;
else if(cur->bf==-1 || cur->bf==1) *info=1;
else
{
firdirection=!direction;
///调试时,发现这里少写了一个等号
// if(cur->child[firdirection]->bf=1) secdirection=0;草,真帅气!原来1==a这样写确实有必要!
if(1==cur->child[firdirection]->bf) secdirection=0;
/
else secdirection=1;
keepbalance(T,firdirection,secdirection);
/
///调试时,发现经过子树平衡操作后,*info不一定都是0,就是那个特殊情况,在setfactor中/
///的那种特殊情况时,这里*info应改为1! 所以代码改如下://
/
// *info=1; 写代码时:这跟插入可不一样啊...该子树平衡了,它父节点的因子比变!
// *info=0;//因此,这还没完还要是0!! ............啊……这里不一定是0!
还是那个特殊情况搞的鬼!//
if(cur->bf==0) *info=0;
else *info=1;
/
}
}
//------------------------------------------------
//-------------变向递归--辅助删点-----------------
char find(AVL *gogal,AVL *p)
{
char info;
AVL tp=NULL;
if(NULL!=(*p)->child[0])
{
info=find(gogal,&((*p)->child[0]));
if(info!=0) return info;
selectforDelete(p,&info,0);
}
else
{
(*gogal)->e=(*p)->e;
tp=(*p)->child[1];
free((*p));
*p=tp;
info=0;
}
return info;
}
//------------------------------------------------
//**************删除操作*************************//
char DeleteAVL(AVL *T,Elemtype e)
{
char info;
AVL tp=NULL;
if(!(*T)) return -1;//原if(!T) return -1;于2011年11月29日8:59:15修改
else if((*T)->e==e)
{
if(NULL!=(*T)->child[1])
{
info=find(T,&((*T)->child[1]));
if(info!=0) return info;
selectforDelete(T,&info,1);
}
else
{
//调试时,发现这样写不对!!!///
// (*T)=(p=(*T)->child[0])-(free((*T)),0);//Just save a variable! 这里出问题
// (*T)=p-(free((*T)),0); 可以
// (*T)=(p=((*T)->child[0]))+(free((*T)),0); 不可以
tp=((*T)->child[0]);
free((*T));
*T=tp;
//调试时,发现这里漏了给info赋值
info=0;
///
}
}
else if((*T)->e>e)
{
info=DeleteAVL(&(*T)->child[0],e);
if(info!=0) return info;
selectforDelete(T,&info,0);
}
else
{
info=DeleteAVL(&(*T)->child[1],e);
if(info!=0) return info;
selectforDelete(T,&info,1);
}
return info;
}
//************************************************//
//*****************JUST FOR TEST************************//
#define MOVE(x) (x=(x+1)%1000)
AVL queue[1000];
void print(AVL p,int i)
{
int front,rear,temp,count;
front=rear=-1; count=temp=0;
queue[MOVE(rear)]=p; count++;
printf("%d\n",i);
while(front!=rear)
{
p=queue[MOVE(front)]; count--;
if(p->child[0]) queue[MOVE(rear)]=p->child[0],temp++;
if(p->child[1]) queue[MOVE(rear)]=p->child[1],temp++;
printf("%d->%d ",p->e,p->bf);
if(count==0)
{
printf("\n");
count=temp;
temp=0;
}
}
printf("\n");
}
//**************************************************//
int main()
{
AVL T=NULL;
int i,nodenum=0;
freopen("input.txt","w",stdout);
nodenum=100;
for(i=0;i<nodenum;i++)
{
InsertAVL(&T,i);
}
print(T,-1);
for(i=0;i<nodenum-1;i++)
{
DeleteAVL(&T,i);
print(T,i);
}
return 0;
}
那个位操作函数,使程序好像很复杂似的,完全可以用一个外部结构体替换!只是我不想用外部变量,尽量在函数内完成吧
由于本人比较笨,写了很长时间~~有什么不正确的,欢迎指正!!!
这些图费了很大功夫才弄好,本来在编辑框里画的好好的,可是一发表,那些图有些就乱了,刚开始我还试着一个一个对照着修改,看最终发现还是不行……最后忽然想到我怎么不在编辑框中截图呢?最后在编辑框中一个一个截图一个一个上传,这样效果好多了!费这么大功夫只为一点:让读者看着舒服,容易理解。
我还想说:开这个博客园以来,也没多长时间,蛋把我气的不浅!每次都是搞好程序,准备到这里写博客时,就是打不开!气死我了!卡死啦!有时候确实是我网速慢,但有时候网速好了也很难打开啊!你说你还是程序员的家园!看你卡的,我都无语了!网速稍微慢点就打不开,就这浪费了我很多时间!我对博客园很失望!!
朋友们,你们感觉呢?