Todays’Goals:
- 到目前为止,我们只处理一种边类型的图
- 如何处理具有多种边类型的(有向)图(又称异构图)?
Heterogeneous Graphs(异构图)
:
-
Relational GCNs
-
Knowledge Graphs
-
Embeddings for KG Completion
1. Heterogeneous Graphs and Relational GCN(RGCN)
1.1 Heterogeneous Graphs
异构图由以下四元组定义:
G
=
(
V
,
E
,
R
,
T
)
G=(V,E,R,T)
G
=
(
V
,
E
,
R
,
T
)
-
具有节点类型的节点
vi
∈
V
v_i \in V
v
i
∈
V
-
具有关系类型
(v
i
,
r
,
v
j
)
∈
E
(v_i,r,v_j) \in E
(
v
i
,
r
,
v
j
)
∈
E
的边 -
节点类型
T(
v
i
)
T(v_i)
T
(
v
i
)
-
关系类型
r∈
R
r\in R
r
∈
R
现实生活中有许多图都是异构图:
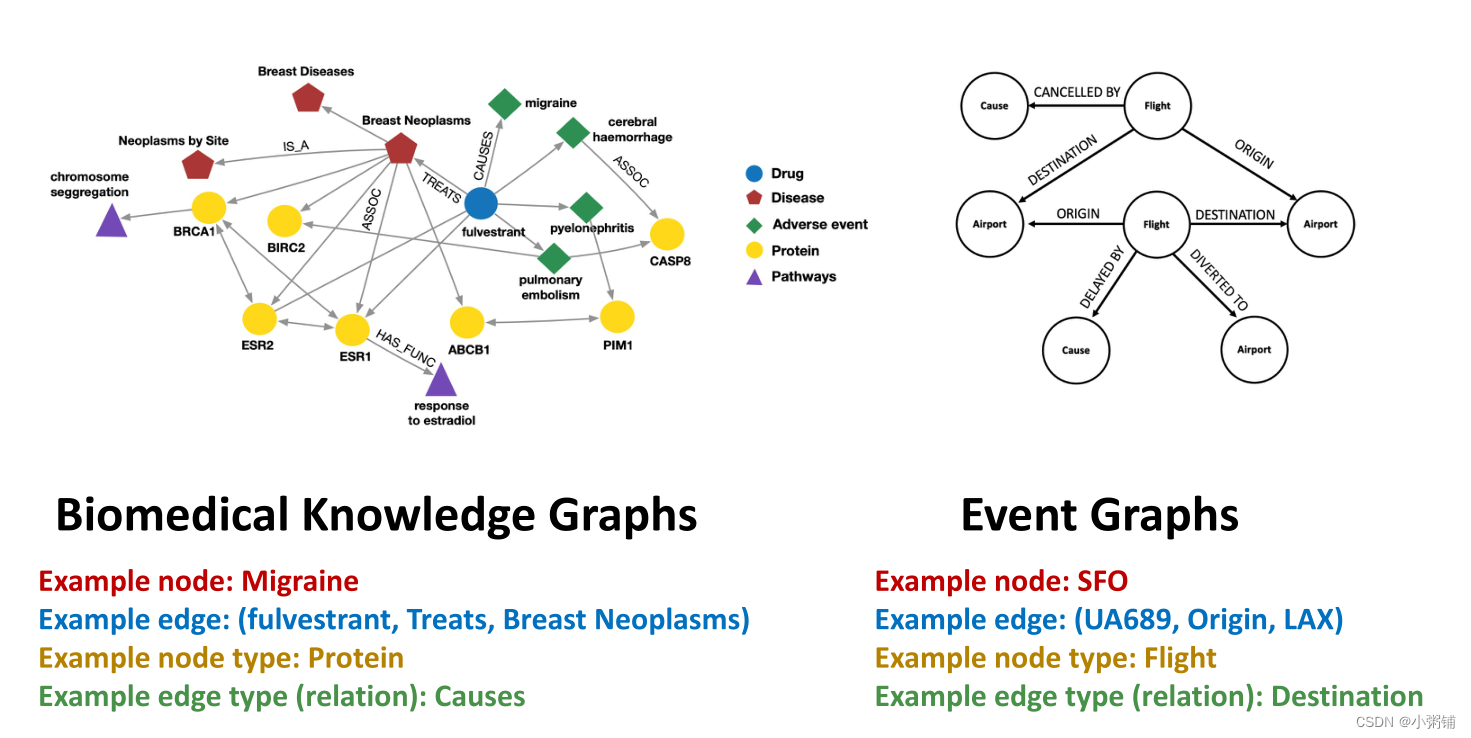
1.2 Relational GCN
我们将扩展GCN来处理具有多种边/关系类型的异构图,我们从一个只有一个关系的有向图开始
-
我们如何运行GCN并更新这个图上目标节点A的表示?
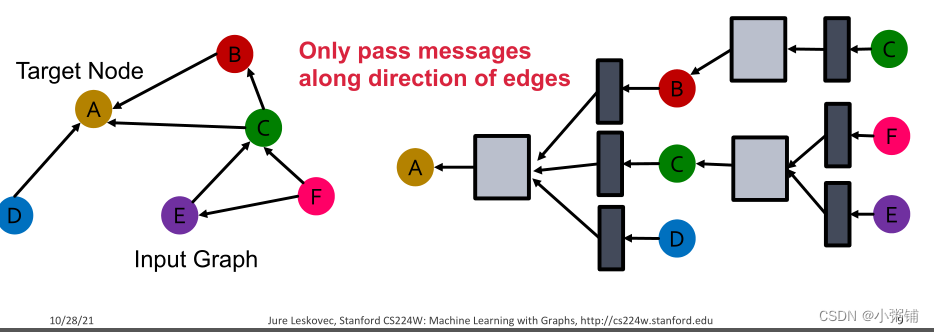
-
A single GNN layer

-
Classical GNN Layers: GCN
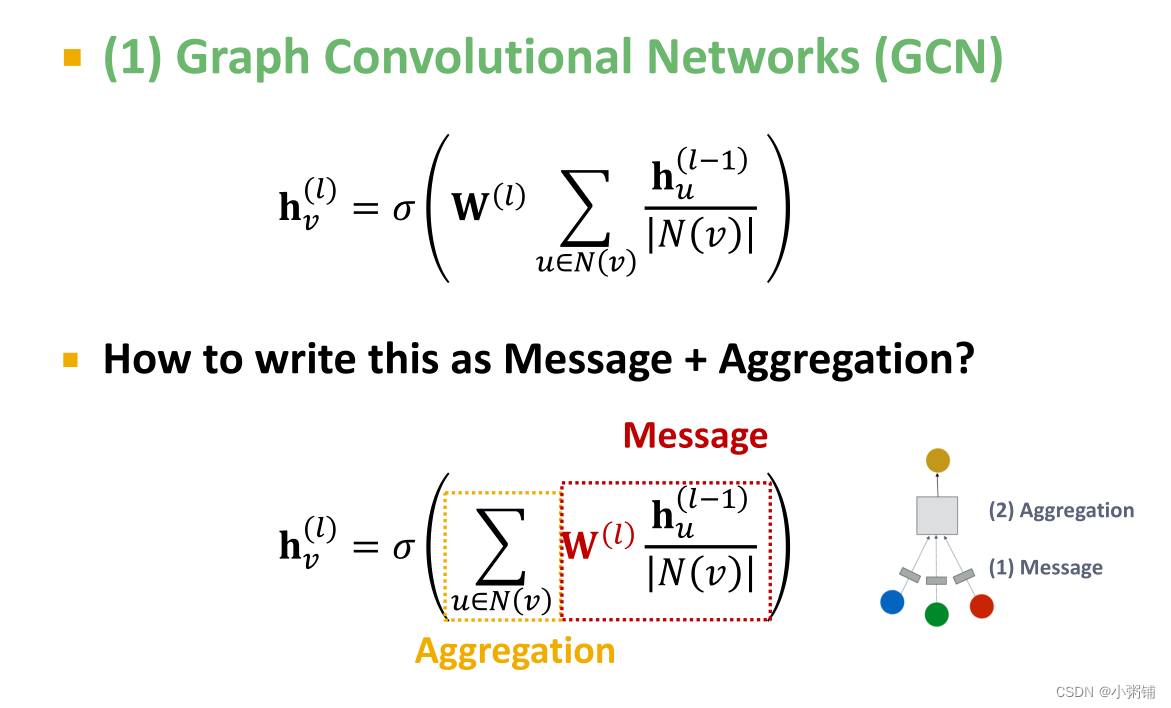
-
Relational GCN
-
如果图形有多种关系类型,则对不同的关系类型使用不同的神经网络权重
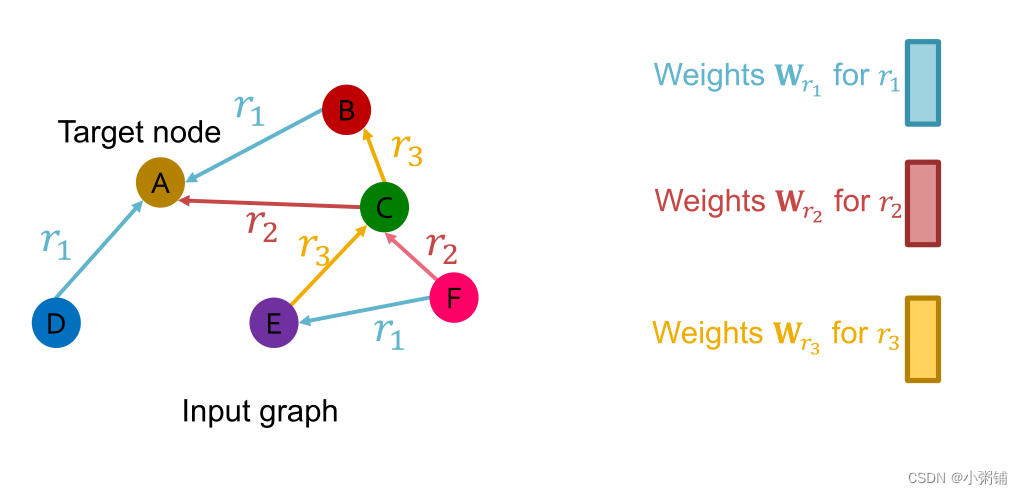
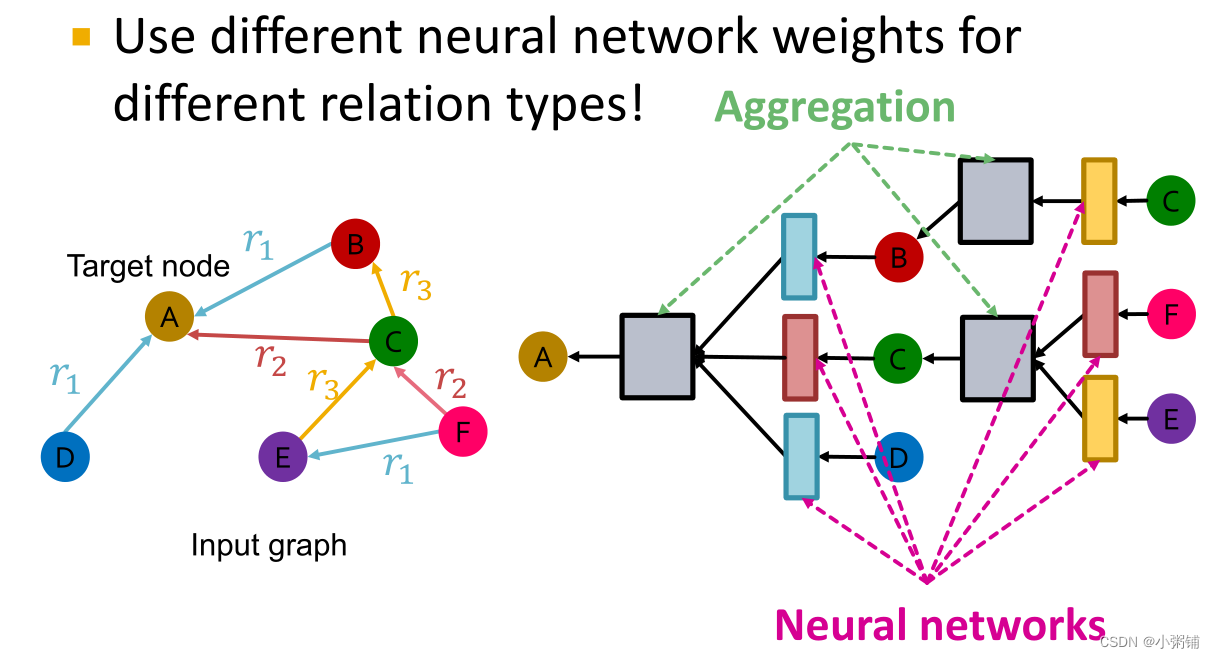
-
如果图形有多种关系类型,则对不同的关系类型使用不同的神经网络权重
-
RGCN的定义
-
Relational GCN(RGCN)
hv
(
l
+
1
)
=
σ
(
∑
r
∈
R
∑
u
∈
N
v
r
1
c
v
,
r
W
r
(
l
)
h
u
(
l
)
+
W
0
(
l
)
h
v
(
l
)
)
h_v^{(l+1)}=\sigma(\sum_{r \in R}\sum_{u \in N_v^r} \frac{1}{c_{v,r}}W_r^{(l)}h_u^{(l)} + W_0^{(l)}h_v^{(l)})
h
v
(
l
+
1
)
=
σ
(
r
∈
R
∑
u
∈
N
v
r
∑
c
v
,
r
1
W
r
(
l
)
h
u
(
l
)
+
W
0
(
l
)
h
v
(
l
)
)
-
Message:
-
给定关系的每个邻居:
mu
,
r
(
l
)
=
1
c
v
,
r
W
r
(
l
)
h
u
(
l
)
m_{u,r}^{(l)}=\frac{1}{c_{v,r}}W_r^{(l)}h_u^{(l)}
m
u
,
r
(
l
)
=
c
v
,
r
1
W
r
(
l
)
h
u
(
l
)
-
Self-loop:
mv
(
l
)
=
W
0
(
l
)
h
v
(
l
)
m_v^{(l)}=W_0^{(l)}h_v^{(l)}
m
v
(
l
)
=
W
0
(
l
)
h
v
(
l
)
-
给定关系的每个邻居:
-
Aggregation:
- 对来自邻居和自循环的消息求和,然后应用激活
-
hv
(
l
+
1
)
=
σ
(
S
u
m
(
{
m
u
,
r
(
l
)
,
u
∈
N
(
v
)
}
∪
{
m
v
(
l
)
}
)
)
h_v^{(l+1)}=\sigma (Sum(\{m_{u,r}^{(l)}, u \in N(v) \}\cup \{ m_v^{(l)}\}))
h
v
(
l
+
1
)
=
σ
(
S
u
m
(
{
m
u
,
r
(
l
)
,
u
∈
N
(
v
)
}
∪
{
m
v
(
l
)
}
)
)
-
Relational GCN(RGCN)
-
RGCN的可拓展性
-
每个关系都有L(L是神经网络的层数)个矩阵:
Wr
(
1
)
,
W
r
(
2
)
.
.
.
W
r
(
L
)
W_r^{(1)},W_r^{(2)}…W_r^{(L)}
W
r
(
1
)
,
W
r
(
2
)
.
.
.
W
r
(
L
)
-
每个
Wr
(
l
)
W_r^{(l)}
W
r
(
l
)
的大小是
d(
l
+
1
)
×
d
(
l
)
d^{(l+1)} \times d^{(l)}
d
(
l
+
1
)
×
d
(
l
)
, 其中
d(
l
)
d^{(l)}
d
(
l
)
是隐藏层l的维数 -
每一层,每一种关系类型都有一个这样的矩阵,参数数量随着不同关系类型的数量而快速增长,会导致
过拟合
问题,同时,模型太大,也会导致无法训练 -
减少RGCN模型参数
Wr
(
l
)
W_r^{(l)}
W
r
(
l
)
的两种方法-
使用
分块对角矩阵
-
Basis/Dictionary learning
-
使用
-
每个关系都有L(L是神经网络的层数)个矩阵:
-
分块对角矩阵
- 关键思想:把权重变稀疏
-
使权重矩阵变稀疏的方式是强制执行,使该矩阵具有对角线结构,变成块对角矩阵
Wr
W_r
W
r
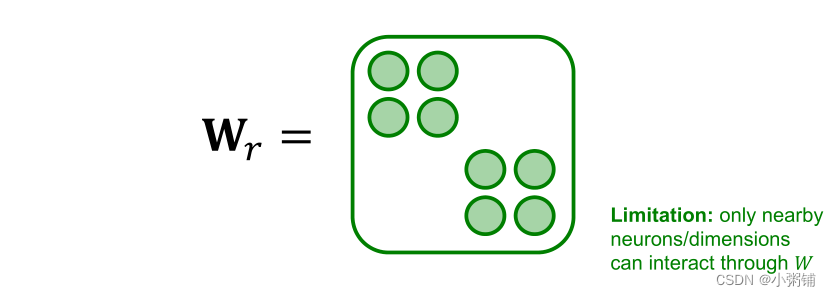
-
如果使用B个低维矩阵,则参数从
d(
l
+
1
)
×
d
(
l
)
d^{(l+1)}\times d^{(l)}
d
(
l
+
1
)
×
d
(
l
)
减少到
B×
d
(
l
+
1
)
B
×
d
(
l
)
B
B \times \frac{d^{(l+1)}}{B} \times \frac{d^{(l)}}{B}
B
×
B
d
(
l
+
1
)
×
B
d
(
l
)
,我们可以更快的训练模型,减少过度拟合,训练出更健壮的模型。 - 但是,使用这种方法,只有附近的神经元或 在同一块中的神经元可以互相交换信息,因此,相距较远的神经元的交流可能需要多层传播,RGCN需要设计得更加深入。
-
Basis Learning
- 关键思想:在不同的关系类型间共享权重。
-
实现共享权重的方法是,将每个关系的矩阵表示为基变换的线性组合
Wr
=
∑
b
=
1
B
a
r
b
⋅
V
b
W_r=\sum_{b=1}^Ba_{rb}\cdot V_b
W
r
=
∑
b
=
1
B
a
r
b
⋅
V
b
,其中
Vb
V_b
V
b
在所有关系中共享-
Vb
V_b
V
b
是基本矩阵,也称为字典,基础学习也被称为字典学习。 -
ar
b
a_{rb}
a
r
b
是矩阵
Vb
V_b
V
b
的重要权重
-
-
现在每个关系只需学习
{a
r
b
}
b
=
1
B
\{a_{rb}\}_{b=1}^B
{
a
r
b
}
b
=
1
B
,即B个标量。
-
RGCN应用于实体/节点分类问题
- 目标:预测给定节点的标签
-
RGCN使用最终层的表示:
-
如果我们从k个类中预测节点A的类型,我们取最后一层(预测头):
hA
(
L
)
∈
R
k
h_A^{(L)} \in \mathbb{R}^k
h
A
(
L
)
∈
R
k
,
hA
(
L
)
h_A^{(L)}
h
A
(
L
)
中每个数代表了每个类别的可能性
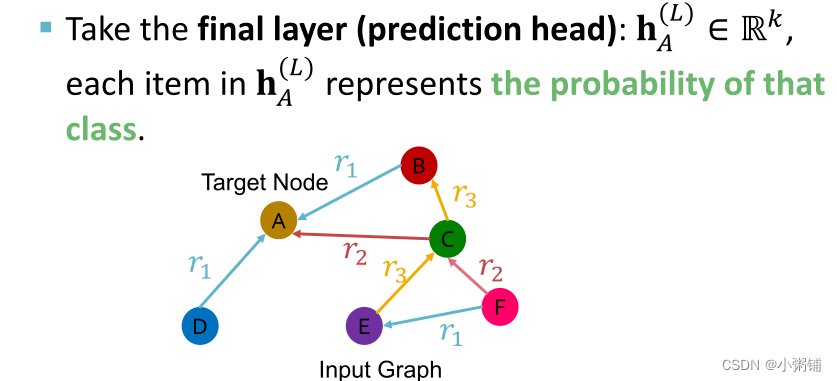
-
如果我们从k个类中预测节点A的类型,我们取最后一层(预测头):
-
RGCN应用于链接预测
- 难点:每个链接具有不同的类型
-
基本思想:链接拆分
对于每一种关系类型,我们将其拆分成训练消息边集、训练监督边集、验证边集、测试边集,然后再合并所有关系类型的这四个集合
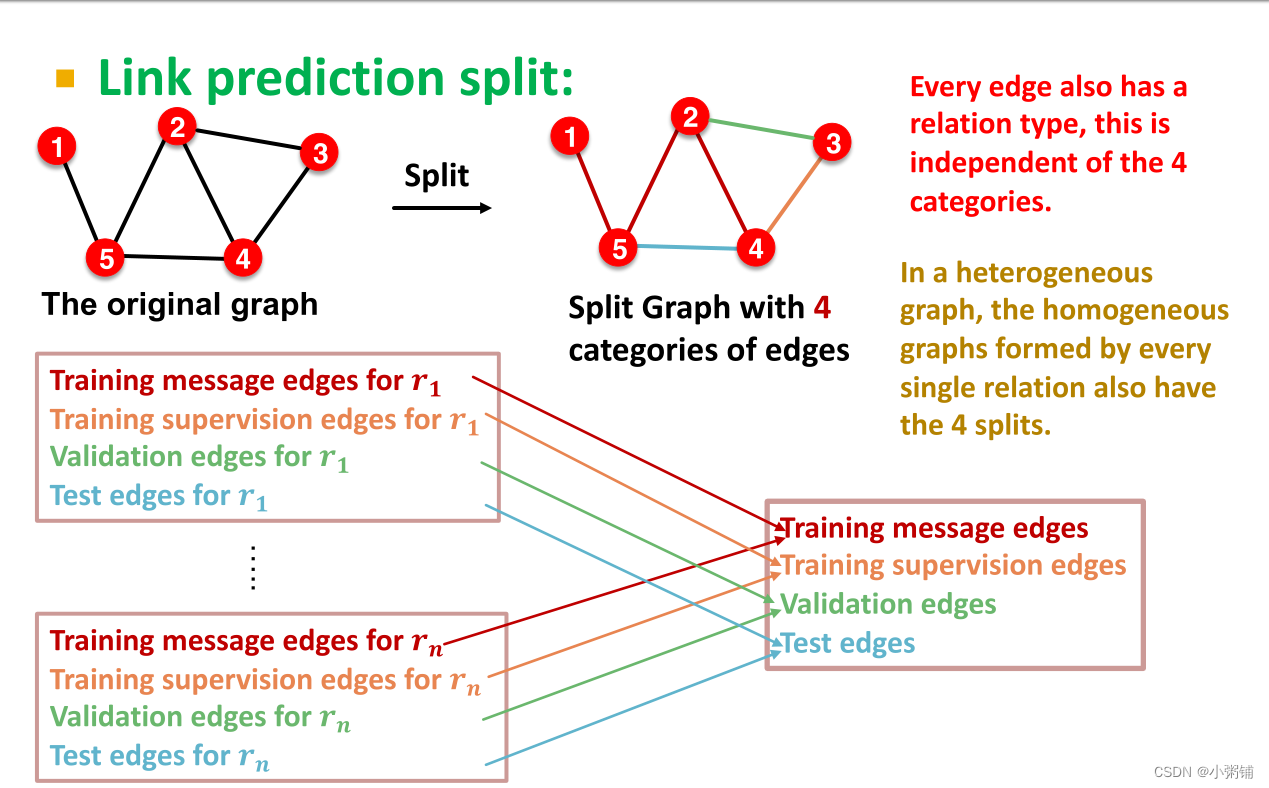
-
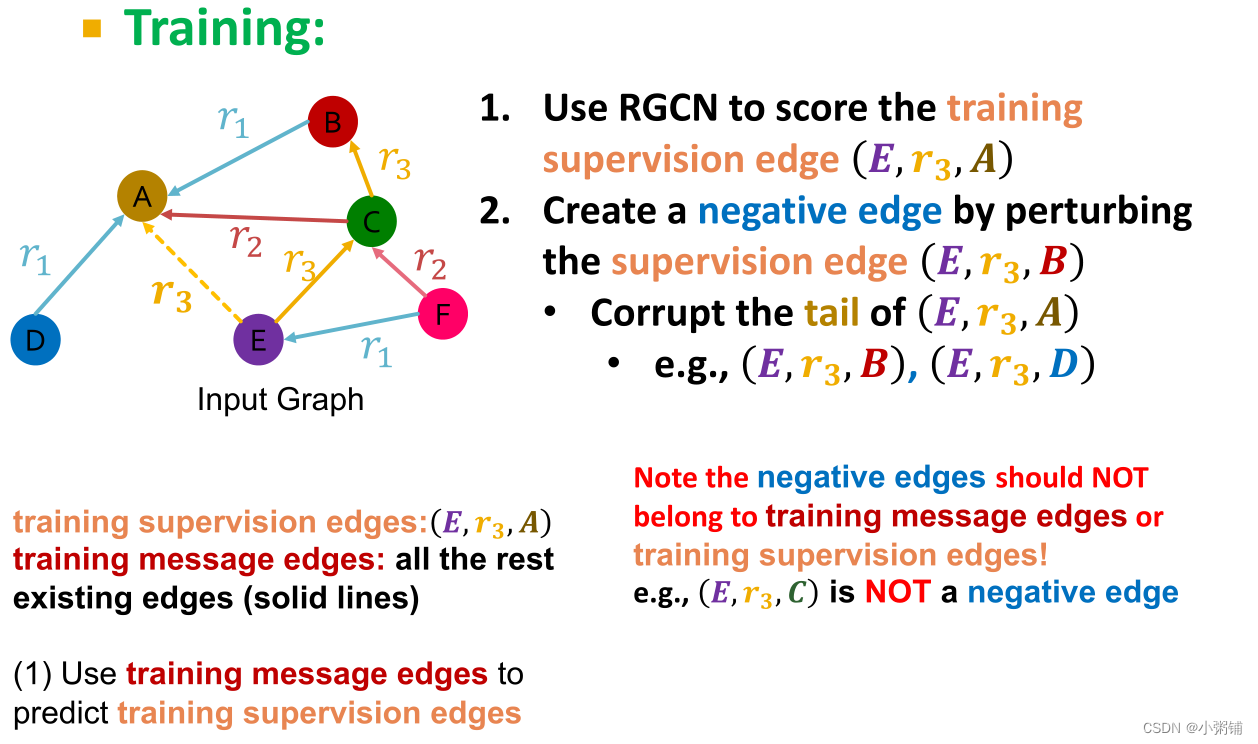
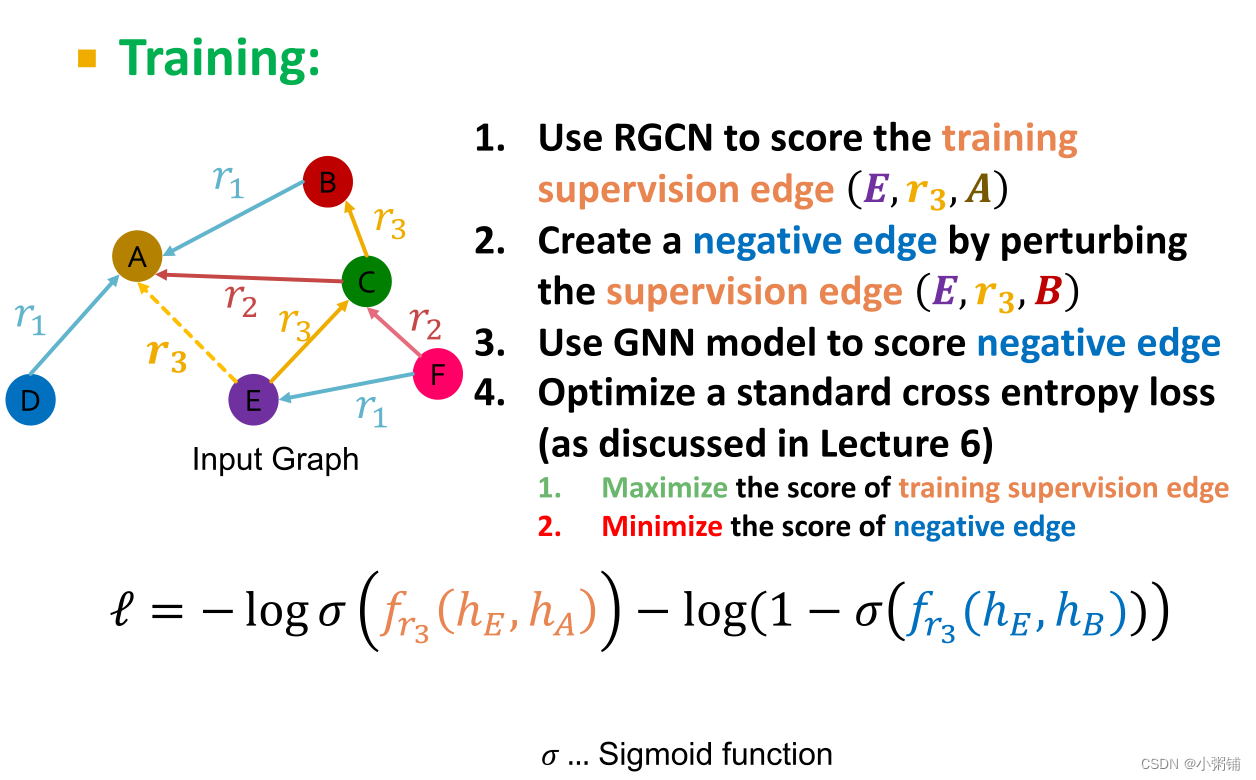
RGCN训练过程
-
边评分函数

-
训练:采用负采样创建负边缘,训练木目标是使得训练监督边的分数尽量高,负边缘的分数尽量低

注意:现有的训练消息边缘或训练监督边缘不能为负边缘。
-
验证


-
边评分函数
-
总结
- 关系GCN是一种用于异构图形的图形神经网络,可以执行实体分类以及链接预测任务。
- 我们可以采用之前的思想扩展RGNN (RGraphSAGE,RGAT等),增强RGCN的准确度。
2. Knowledge Graphs: KG Completion with Embedding
2.1 Knowledge Graphs (KG)
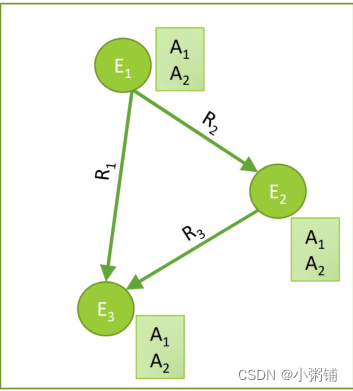
知识图谱是图形式的知识,它捕获实体,类型和关系。
- 节点是实体
- 节点用它们的类型标记
- 两个节点之间的边捕获实体之间的关系
-
KG是异构图的一个实例
Example:
-
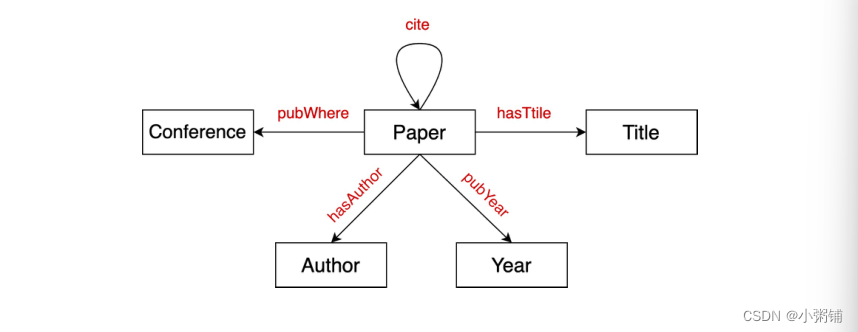
文献网络
- 节点类型:论文、标题、作者、会议、年份
-
关系类型:pubWhere、pubYear、hasTitle、hasAuthor、cite
-
生物知识网络
- 节点类型:药物、疾病、不良事件、蛋白质、途径
-
关系类型:has_func、causes、assoc、treats、is_a
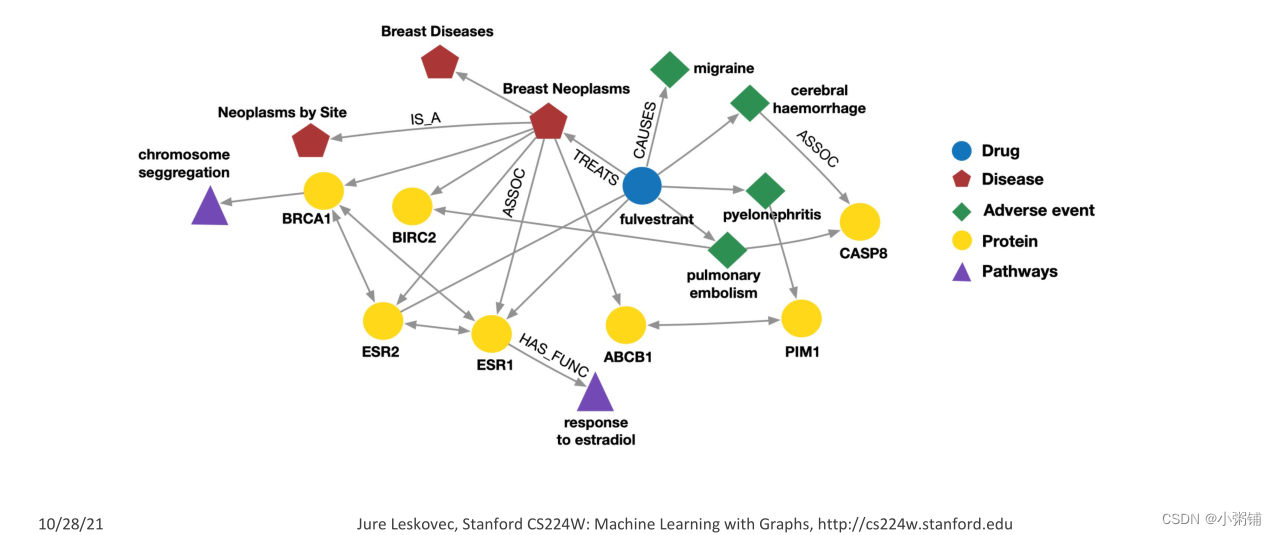
-
文献网络
实践中的知识图谱:
- 谷歌知识图
- 亚马逊产品图
- Facebook Graph API
- IBM Watson
- 微软Satori
- Project Hanover/Literome
- LinkedIn Knowledge Graph
- Yandex Object Answer
知识图谱的应用:
-
提供信息
-
问答和对话代理
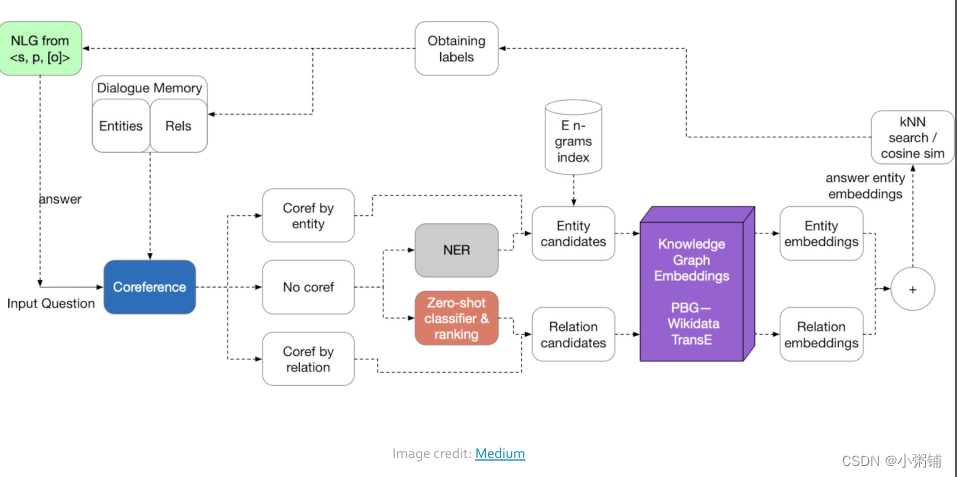
知识图谱数据集:
现在有许多公开可用的知识图谱数据集,例如FreeBase, Wikidata, Dbpedia, YAGO, NELL等,这些数据集有两个共同的特点,- 庞大,有数百万个节点和边
-
不完整:许多真正的边丢失
Example: Freebase
-
Freebase
- 约8000万个实体
- 约38K个关系类型
- 约30亿个事实/三元组
- 但是,还有93.8%来自Freebase的人没有出生地,78.5%没有国籍!显然,这些知识图是不完整的
-
Datasets:FB15k/FB15k-237
-
是Freebase的完整子集,研究人员用来学习KG模型

-
是Freebase的完整子集,研究人员用来学习KG模型
2.2 Knowledge Graph Completion: TransE,TransR,DistMul,ComplEx
2.2.1 KG Completion Task
任务
:对于给定的(头部,关系),我们预测丢失的尾部
– 请注意,这与经典的链接预测任务略有不同,这里我们只对特定节点的特定关系感兴趣
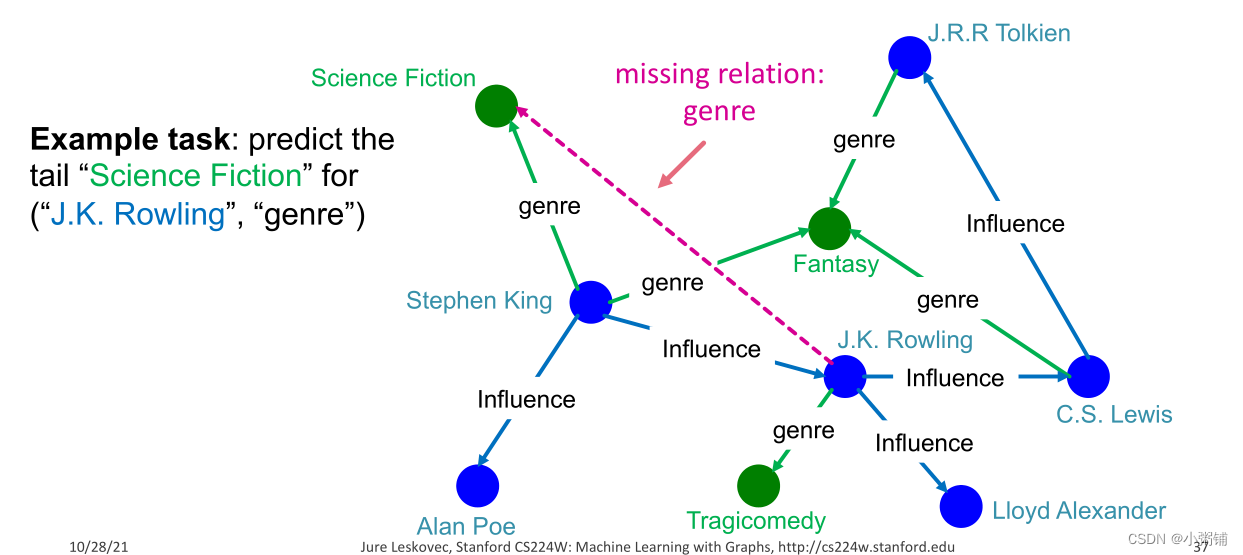
-
这里我们使用
浅层编码器
计算每个节点的嵌入 -
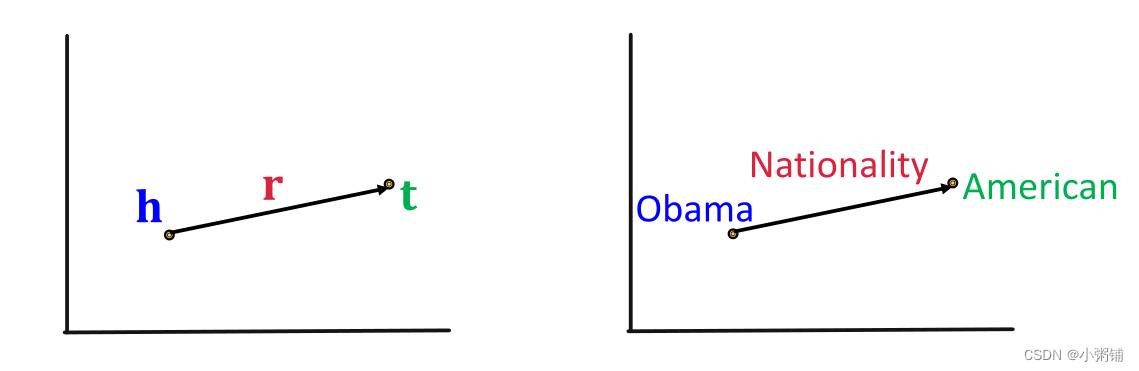
KG Representation
-
知识图谱中的边被表示成一个
三元组(h, r ,t)
,即head
(h
)
(h)
(
h
)
has relation
(r
)
(r)
(
r
)
with tail
(t
)
(t)
(
t
)
-
key Idea
-
对嵌入/向量空间
Rd
\mathbb{R^d}
R
d
中的实体和关系进行建模:用浅嵌入关联实体和关系。注意,我们在这里学习的不是GNN! -
给定一个真正的三元组
(h
,
r
,
t
)
(h,r,t)
(
h
,
r
,
t
)
,
目标是
(h
,
r
)
(h,r)
(
h
,
r
)
的嵌入应该接近于
tt
t
的嵌入
-
如何嵌入
(h
,
r
)
(h,r)
(
h
,
r
)
?
-
如何定义closeness?
-
-
对嵌入/向量空间
-
知识图谱中的边被表示成一个
2.2.2 TransE
-
Translation Intuition: 对于一个三元组
(h
,
r
,
t
)
(h,r,t)
(
h
,
r
,
t
)
,
h,
r
,
t
∈
R
d
h,r,t \in \mathbb{R^d}
h
,
r
,
t
∈
R
d
,如果存在这样的关系
h+
r
≈
t
h + r \approx t
h
+
r
≈
t
,否则,
h+
r
≠
t
h + r \neq t
h
+
r
=
t
,评分函数为:
fr
(
h
,
t
)
=
−
∣
∣
h
+
r
−
t
∣
∣
f_r(h,t) = -||h + r -t||
f
r
(
h
,
t
)
=
−
∣
∣
h
+
r
−
t
∣
∣
-
TransE学习算法:实体和关系被统一初始化并规范化,
负采样
KG中未出现的三元组,采用
对比损失
,
训练目标
是
对于有效的三元组,倾向于较低的距离(或较高的分数),对于损坏的三元组,倾向于较高的距离(或较低的分数)

那么,这种方法可以学习什么样的关系呢?在知识图谱中,关系具有不同的属性。 -
KG中的连接模式
-
异构KG中的关系具有不同的属性,比如:
-
对称/反对称关系
r(
h
,
t
)
⇒
r
(
t
,
h
)
(
r
(
h
,
t
)
⇒
¬
r
(
t
,
h
)
)
∀
h
,
t
r(h,t)\Rightarrow r(t,h)\quad (r(h,t)\Rightarrow ¬r(t,h))\quad \forall h,t
r
(
h
,
t
)
⇒
r
(
t
,
h
)
(
r
(
h
,
t
)
⇒
¬
r
(
t
,
h
)
)
∀
h
,
t
-
逆关系:如果边
(h
,
”
A
d
v
i
s
o
r
”
,
t
)
(h,”Advisor”,t)
(
h
,
”
A
d
v
i
s
o
r
”
,
t
)
在KG中存在,那么边
(t
,
”
A
d
v
i
s
e
e
”
,
h
)
(t,”Advisee”,h)
(
t
,
”
A
d
v
i
s
e
e
”
,
h
)
在KG中也存在 -
复合(传递)关系:
r1
(
x
,
y
)
∧
r
2
(
y
,
z
)
⇒
r
3
(
x
,
z
)
∀
x
,
y
,
z
r_1(x,y)\wedge r_2(y,z)\Rightarrow r_3(x,z)\quad \forall x,y,z
r
1
(
x
,
y
)
∧
r
2
(
y
,
z
)
⇒
r
3
(
x
,
z
)
∀
x
,
y
,
z
,例如,我妈妈的丈夫是我的爸爸 -
一对多关系
r(
h
,
t
1
)
,
r
(
h
,
t
2
)
,
.
.
.
,
r
(
h
,
t
n
)
r(h,t_1),r(h,t_2),…,r(h,t_n)
r
(
h
,
t
1
)
,
r
(
h
,
t
2
)
,
.
.
.
,
r
(
h
,
t
n
)
are all True,例如,r是Studentsof的关系
-
- 我们能对这些关系模式进行分类吗?
- KG嵌入方法(例如TransE)的表达能力是否足以对这些模式进行建模?
-
异构KG中的关系具有不同的属性,比如:
-
关系模式 (Relation Patterns)
-
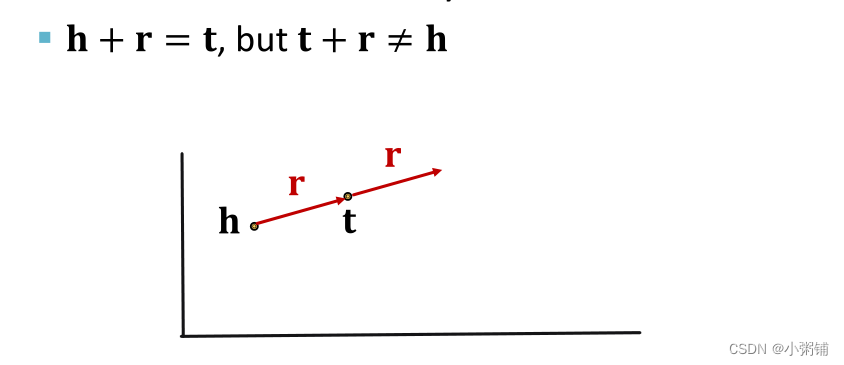
TransE中的反对称关系
-
(r
(
h
,
t
)
⇒
¬
r
(
t
,
h
)
)
∀
h
,
t
(r(h,t)\Rightarrow ¬r(t,h))\quad \forall h,t
(
r
(
h
,
t
)
⇒
¬
r
(
t
,
h
)
)
∀
h
,
t
- example: 上位词
-
TransE可以建模反对称关系
-
-
TransE中的逆关系
-
TransE可以建模逆关系
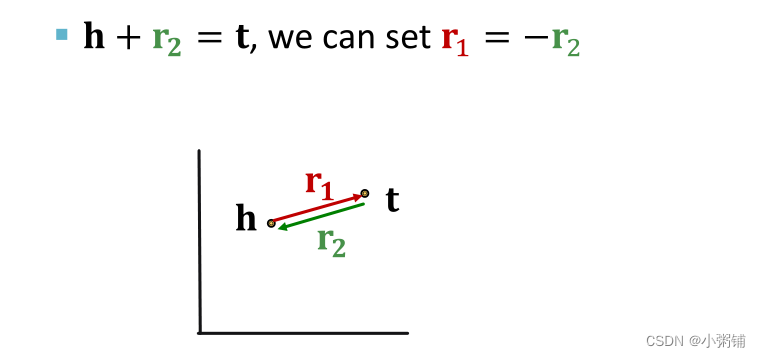
-
TransE可以建模逆关系
-
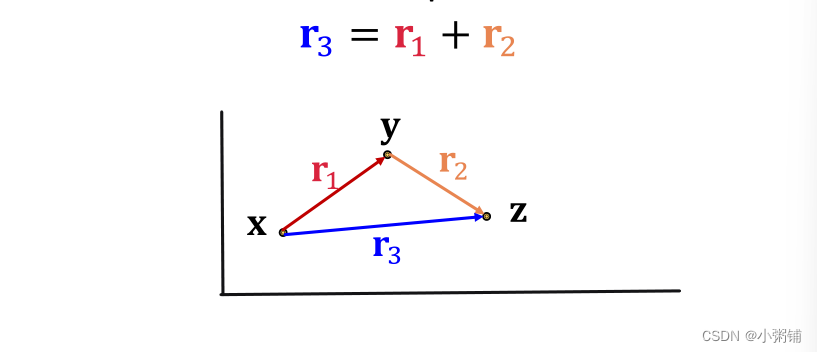
TransE中的复合关系
-
TransE可以建模复合关系
-
TransE可以建模复合关系
-
TransE的局限 :对称关系
-
TransE不可以建模对称关系

-
TransE不可以建模对称关系
-
TransE的局限 :一对多关系
-
TransE不可以建模一对多关系

-
TransE不可以建模一对多关系
-
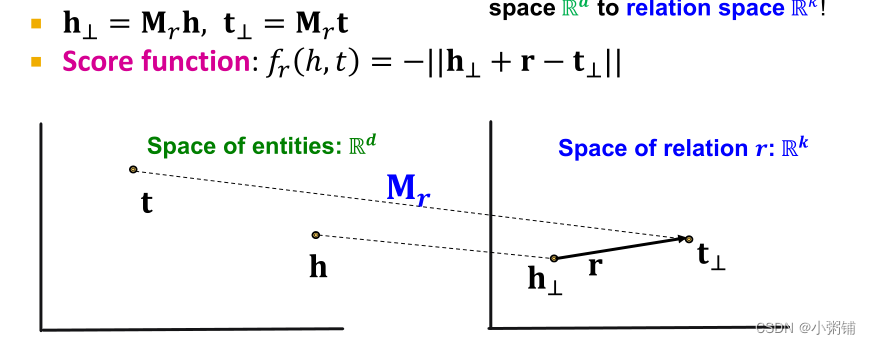
2.2.3 TransR
TransE中任何关系的平移都在同一嵌入空间中进行建模。TransR将实体建模为实体空间
R
d
\mathbb{R}^d
R
d
中的向量,并将每个关系建模为具有投影矩阵
M
r
∈
R
k
×
d
M_r\in \mathbb{R}^{k \times d}
M
r
∈
R
k
×
d
的关系空间
r
∈
R
k
r \in \mathbb{R}^k
r
∈
R
k
中的向量,使用
M
r
M_r
M
r
将实体向量从实体空间
R
d
\mathbb{R}^d
R
d
投影到关系空间
R
k
\mathbb{R}^k
R
k
。
-
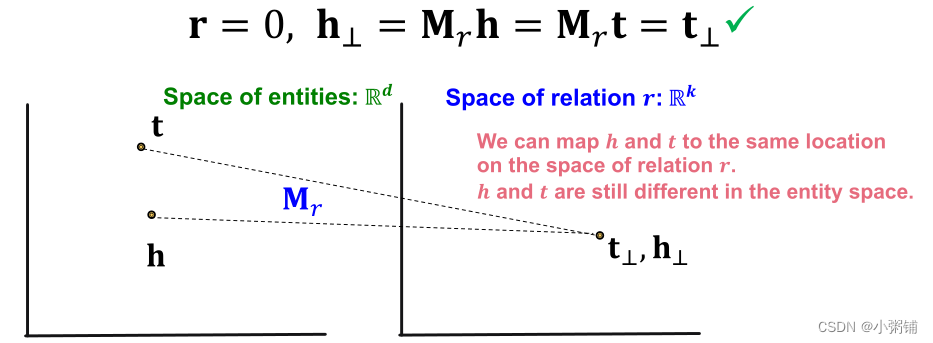
TransR中的对称关系
TransR可以建模对称关系,他将具有对称关系的两个实体映射到关系空间上的同一位置,这两个节点在实体空间里仍然是不同的实体。注意:不同的对称关系可能有不同的对称矩阵。
-
TransR中的反对称关系
TransR可以建模反对称关系。

-
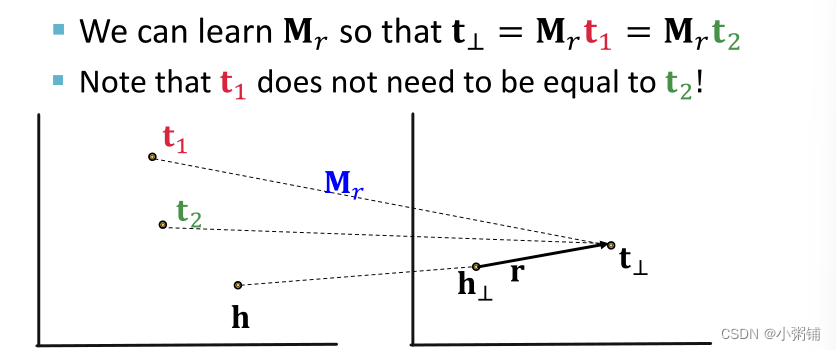
TransR中的一对多关系
TransR可以建模一对多关系。TransR学习矩阵
Mr
M_r
M
r
使得
t1
t_1
t
1
,
t2
t_2
t
2
映射到关系空间的同一点。
-
TransR中的逆关系
TransR可以建模逆关系。
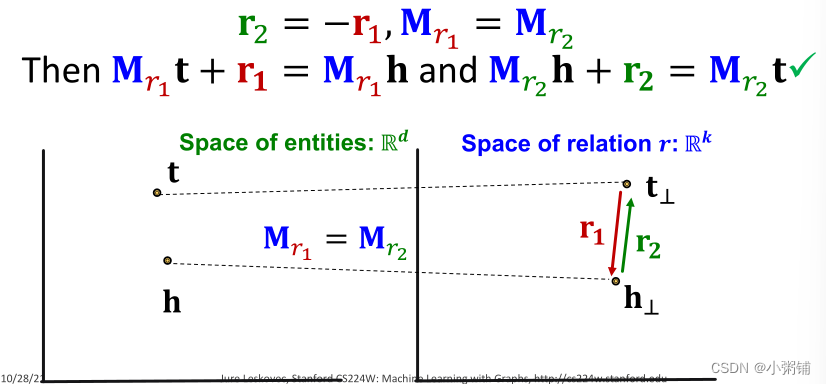
-
TransR中的复合关系
TransR可以建模复合关系。TransR用线性函数对三元组进行建模,它们是可链接的。
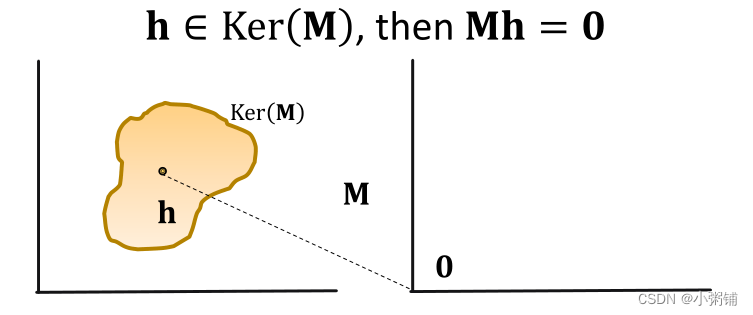
背景知识:矩阵
MM
M
的核空间
组合关系:
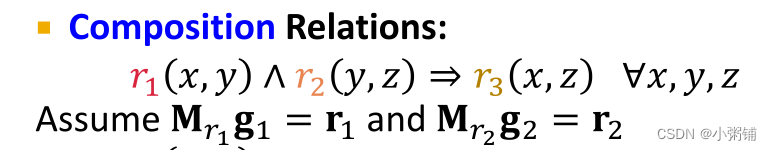
可以推出:
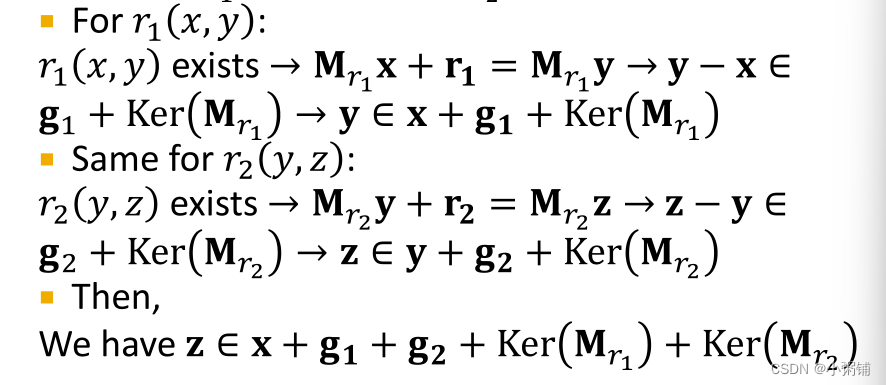
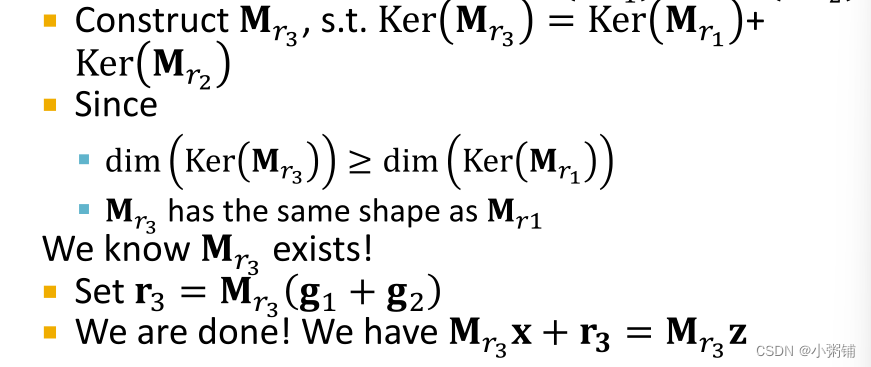
因此,TransR可以建模组合关系。
2.2.4 DistMult
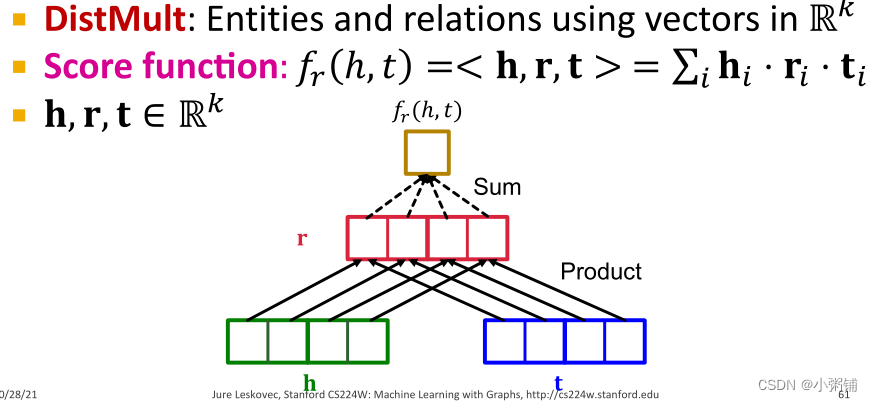
-
新的思想:双线性模型
TransE和TransR中的的评分函数
fr
(
h
,
t
)
f_r(h,t)
f
r
(
h
,
t
)
是L1/L2距离的负值,另一种KG嵌入方法DistMult采用双线性建模:实体和关系是空间
Rk
\mathbb{R}^k
R
k
中的向量,评分函数
fr
(
h
,
t
)
=
<
h
,
r
,
t
>
=
∑
i
h
i
⋅
r
i
⋅
t
i
f_r(h,t)=<h,r,t>=\sum_ih_i \cdot r_i \cdot t_i
f
r
(
h
,
t
)
=
<
h
,
r
,
t
>
=
∑
i
h
i
⋅
r
i
⋅
t
i
,
h,
r
,
t
∈
R
k
h,r,t \in \mathbb{R}^k
h
,
r
,
t
∈
R
k
。
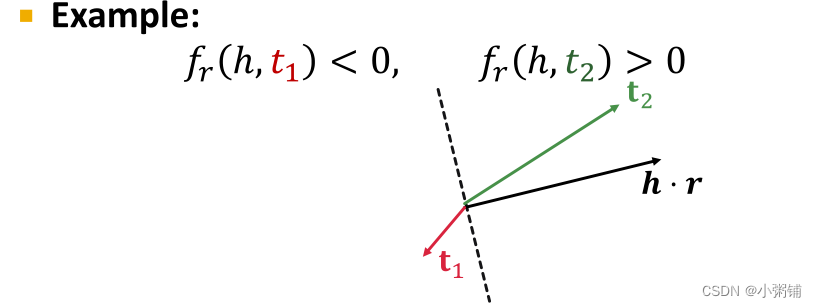
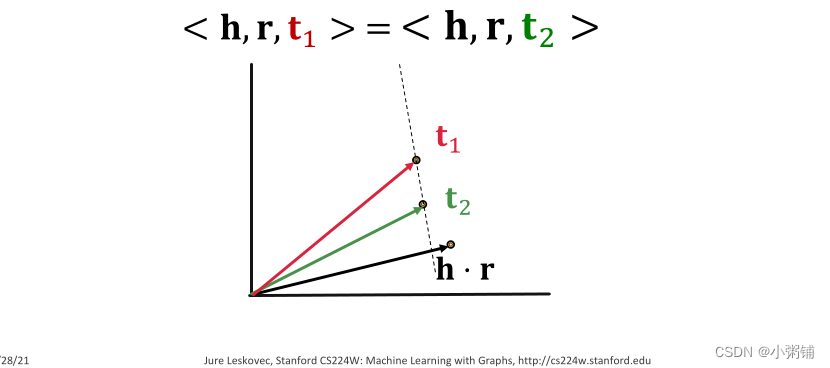
这里的评分函数可以看作
h⋅
r
h \cdot r
h
⋅
r
和
tt
t
的余弦相似性,
h⋅
r
h \cdot r
h
⋅
r
定义了一个超平面,
h⋅
r
=
∑
i
h
i
⋅
r
i
h \cdot r = \sum_ih_i \cdot r_i
h
⋅
r
=
∑
i
h
i
⋅
r
i
。
-
DistMult中的一对多关系
DistMult可以建模一对多关系。
-
DistMult中的对称关系
DistMult可以自然的建立对称关系。
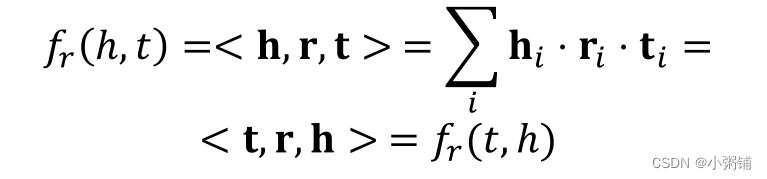
-
DistMult的局限:反对称关系
DistMult无法建模反对称关系。在DistMult的评分函数下,
r(
h
,
t
)
r(h,t)
r
(
h
,
t
)
和r(t,h)总是具有相同的分数。
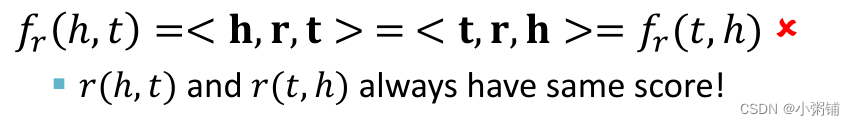
-
DistMult中的局限:逆关系
DistMult无法建模逆关系,形式上,它可以建模
r2
=
r
1
r_2=r_1
r
2
=
r
1
的逆关系,但从语义上讲,这是没有意义的:“Advisor”的嵌入不应与“Advisee”相同

-
DistMult中的局限:组合关系
DistMult无法建模组合关系,DistMult为每个(head,relation)定义了一个超平面,但是由多跳关系引起的超平面的并集(例如
(r
1
,
r
2
)
(r_1, r_2)
(
r
1
,
r
2
)
)不再是超平面。
这里的超平面不太懂
2.2.5 ComplEx
基于Distmult,ComplEx在复向量空间中嵌入实体和关系。
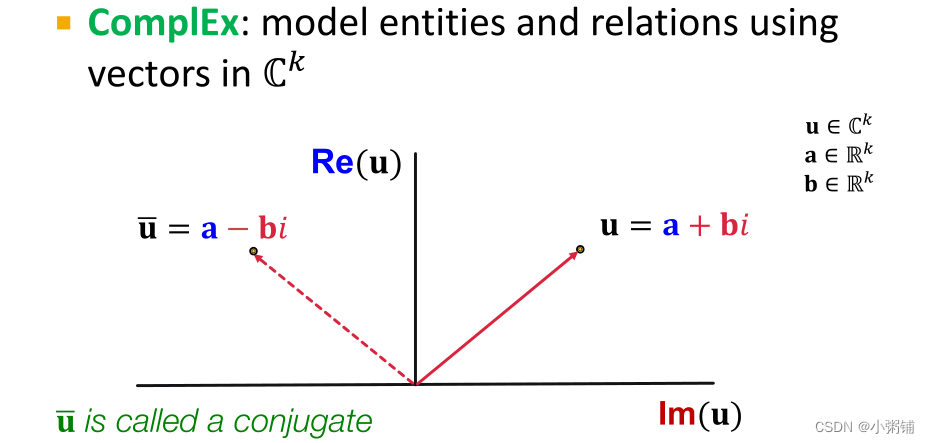
注:
u
ˉ
\bar{u}
u
ˉ
和u互为共轭复数。
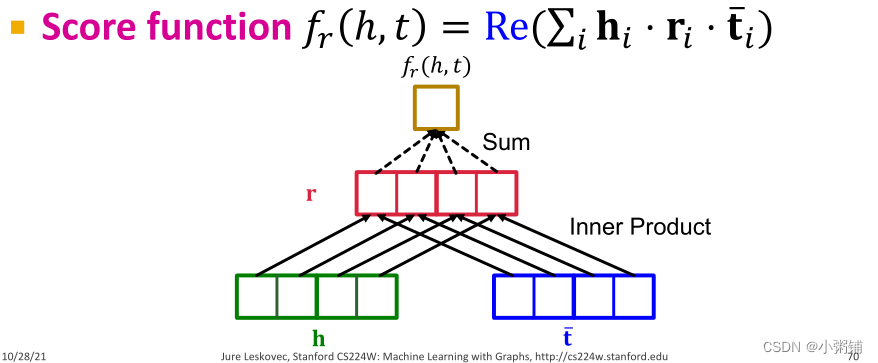
ComplEx的评分函数
f
r
(
h
,
t
)
=
R
e
(
∑
i
h
i
⋅
r
i
⋅
t
i
ˉ
)
f_r(h,t)=Re(\sum_ih_i \cdot r_i \cdot \bar{t_i})
f
r
(
h
,
t
)
=
R
e
(
∑
i
h
i
⋅
r
i
⋅
t
i
ˉ
)
,
R
e
(
⋅
)
Re(\cdot)
R
e
(
⋅
)
表示取复数的实部。
-
ComplEx中的反对称关系
ComplEx可以用共轭复数建模反对称关系。

-
ComplEx中的对称关系
ComplEx可以建模对称关系。我们可以设r的虚部为0,有:
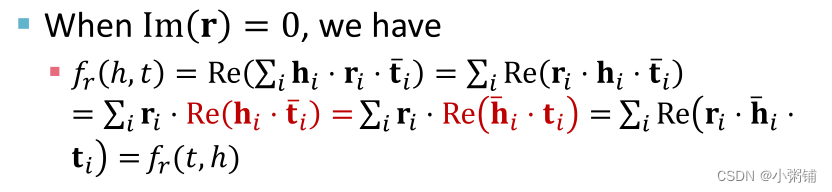
-
ComplEx中的逆关系
通过令
r1
=
r
2
ˉ
r_1=\bar{r_2}
r
1
=
r
2
ˉ
,ComplEx可以建模逆关系。
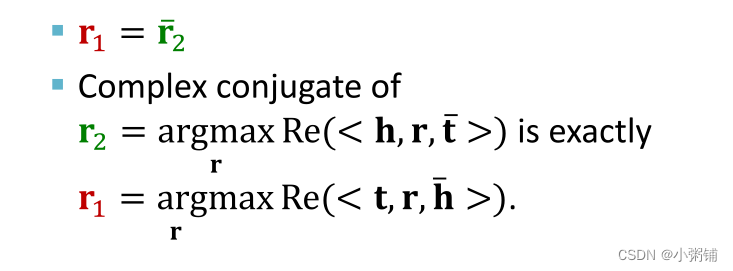
-
ComplEx中的组合关系和一对多关系
CompleEx与DistMult共享相同的属性,无法建模组合关系可以建立一对多关系。
-
2.2.6 Summary
不同KG完成方法的特性和表现力:
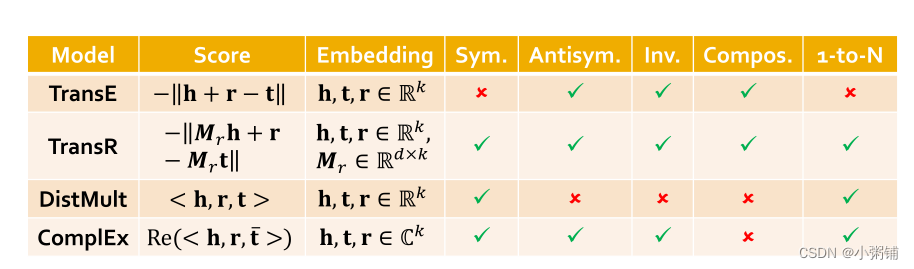
- 不同的KG可能有截然不同的关系模式!
- 2.没有适用于所有KG的通用嵌入,我们可以依据上面的表格选择模型
- 3.如果目标KG没有太多对称关系,可以尝试TransE快速运行
-
4.然后再使用更具表现力的模型,例如CompleEx、RotatE(
复杂空间中的TransE
)