1.问题描述
角谷猜想在西方常被称为西拉古斯猜想,据说这个问题首先是在
美国的西拉古斯大学被研究的,而在东方,这个问题则由将它带到日
本的日本数学家角谷静夫的名字来命名,故被称为角谷猜想。
角谷猜想的内容是任给一个自然数,若为偶数则除以2,若为奇数
则乘以3再加1,这样得到一个新的自然数之后再按照前面的法则继续
演算,若干次以后得到的结果必然为1。在数学文献里,角谷猜想也常
常被称为“3X+1问题”。请编程验证角谷猜想。
2.问题分析
先通过几个实例来理解角谷猜想的含义。
取自然数n=6,则根据角谷猜想,有:
6→3→10→5→16→8→4→2→1。
最终结果为1,则n=6时角谷猜想成立。
取自然数n=15,则根据角谷猜想,有:
15→46→23→70→35→106→53→160→80→40→20→10→5→16→
8→4→2→1。
最终结果为1,则n=15时角谷猜想成立。
读者还可取其他的自然数按照上述规则来演算,结果都为1。
虽然角谷猜想还未获得一般的证明,但是已经有人拿各种各样的
数字来进行试验,结果发现角谷猜想总是成立的,现在已经获得验证
的最大数是1 099 511 627 776。
3.算法分析
角谷猜想中已经明确地给出了处理过程,即对于给定的自然数n,
有如下函数:
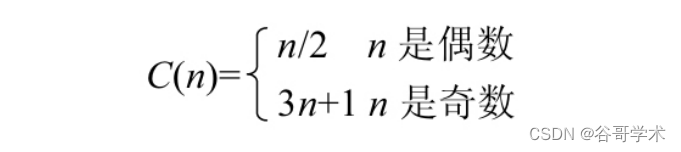
在问题分析中进行的变换,实际上是对函数C进行迭代。则问题可
表述为:从任意一个自然数开始,经过对函数C有限次的迭代,能否最
终得到1。
算法不需要特别的设计,根据函数C可直接进行角谷猜想的验证。
4.确定程序框架
在main()函数中构建一个不定次数的while循环。定义变量n表示输
入的自然数,在循环体中判断n的奇偶性并根据奇偶性的不同执行不同
的操作,当n=1时,退出while循环。while循环结构如下:
while n != 1: # 当n=1时终止循环
# 若n为奇数,则乘以3加1
if n % 2 == 1:
n = n * 3 + 1
count += 1
# 输出执行步骤
print("[%d]: %d * 3 + 1 = %d "
%(count, (n-1)//3, n))
else:
n //= 2 # 若n为偶数,则直接除以2
count += 1
print("[%d]: %d / 2 = %d " %(count,
2 * n, n)) # 输出执行步骤程序的流程图如图10.9所示。
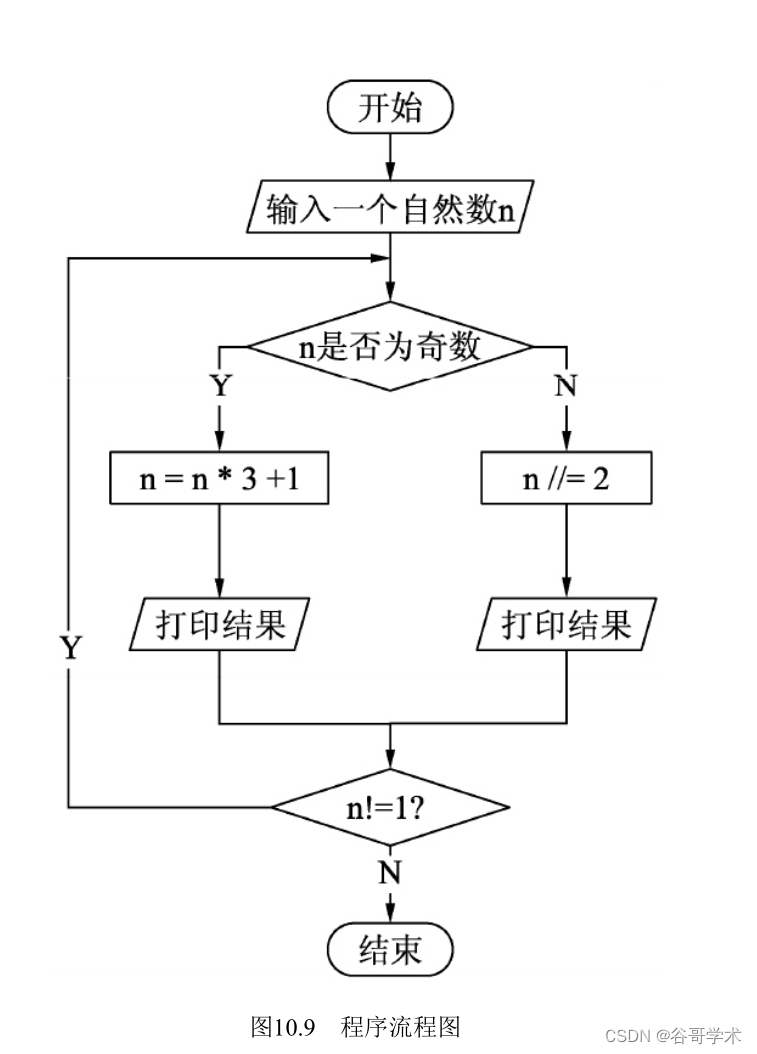
5.完整的程序
根据上面的分析,编写完整的程序如下:
#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @author : liuhefei
# @desc: 角谷猜想
# 任给一个自然数,若为偶数则除以2,若为奇数则乘以3再加1
# 这样得到一个新的自然数之后再按照前面的法则继续演算,若干次以后得到的结果必然为1
if __name__ == "__main__":
count = 0
n = int(input("请输入一个自然数:"))
while n != 1: # 当n=1时终止循环
if n % 2 == 1: # 若n为奇数,则乘以3加1
n = n * 3 + 1
count += 1
# 输出执行步骤
print("[%d]: %d * 3 + 1 = %d " %(count, (n-1)//3, n))
else:
n //= 2 # 若n为偶数,则直接除以2
count += 1
print("[%d]: %d / 2 = %d " %(count, 2 * n, n)) # 输出执行步骤
6.运行结果
在PyCharm下运行程序,结果如图10.10所示。在图10.10a中打印出
了n=6时按照角谷猜想的执行步骤,最后结果为1;在图10.10b中打印出
了n=15时按照角谷猜想的执行步骤,最后结果也为1。因此,它们都符
合角谷猜想的结论。读者也可以任意输入其他自然数进行验证。
