博客

Problem – 7150 (hdu.edu.cn)

题意：

给你一个n个节点的树，现在有q次询问，每次询问会先从树中选几个点构成集合A，然后再选几个构成集合B，再选几个构成集合C，问树上有多少个点满足：

这个点，是集合A中某个点到集合C中某个点的最短路径上的点，并且是集合B中某个点到集合C中某个点的最短路径上的点

知识点：树刨（本来就是来写树刨的

思路：

对于某一次查询，在这次查询的集合A中的点，我们把这些点到树根的路径上的点都打上标记，然后对于这次查询的集合B中的点，我们同样把这些点到树根的路径上的点都打上标记，

对于这次查询的集合C中的点，我们把这些点的所有子树都打上标记，

最后，这次查询的答案，就是整个树上同时有A,B,C标记的点

A,B集合为什么走到根？

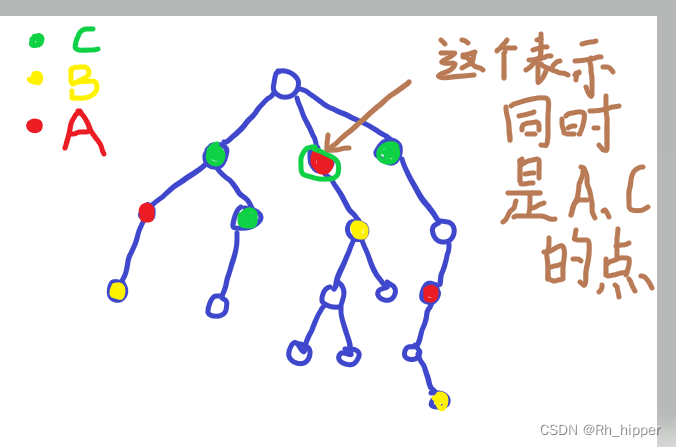
标记完后

其实挺显然的，走到树根不会出现多余的贡献，而且简化了操作，因为我们要三个集合都走到过，而集合C是走子树，所以其实最后答案都在集合C的子树中，如果我们A,B集合中某两点一直往上走产生了贡献，说明一定有一个点属于集合C，是他们的祖先或者本身。

具体的代码的话，本人写的挺多的，虽然逻辑清楚，但是还是码了300多行。。。。（可能是刚学树刨想的比较复杂？）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N= 2e5 + 5;
const int mod = 1e9+7;
#define ls (i<<1)
#define rs ((i<<1)|1)
int dfn[N],siz[N],son[N],boc[N];//这些都是树刨的
int top[N],fa[N],deep[N],rk[N];//
int cnt;
vector<int>mp[N];//记录树的
ll n,m;
int Aa[N],Bb[N],Cc[N];//每次的A,B,C集合
struct tre{
    ll a,ab,abc,l,r,ra,rb,rc;
    //a这个区间有A标记的个数,ra是有a标记的lazy
    //ab这个区间有AB标记的个数,rb是有b标记的lazy
    //abc这个区间有ABC标记的个数.rc是有c标记的lazy
    //l,r是区间的端点
}tree[N<<2];

//这个区间有a lazy,那标记个数就是区间大小
void work_downA(tre &nowtre,ll lazy){
    if(lazy==1)nowtre.a=nowtre.r-nowtre.l+1;//lazy是1表示有 a 要下传
    else nowtre.a=0;//lazy是2表示有 清空a 要下传
    nowtre.ra=lazy;
}
//这个区间有ab lazy,那标记个数就是标记a的个数
void work_downB(tre &nowtre,ll lazy){
    if(lazy==1)nowtre.ab=nowtre.a;//lazy是1表示有 ab 要下传
    else nowtre.ab=0;//lazy是2表示有 清空ab 要下传
    nowtre.rb=lazy;
}
//这个区间有abc lazy,那标记个数就是标记ab的个数
void work_downC(tre &nowtre,ll lazy){
    if(lazy==1)nowtre.abc=nowtre.ab;//lazy是1表示有 abc 要下传
    else nowtre.abc=0;//lazy是2表示有 清空abc 要下传
    nowtre.rc=lazy;
}

void work_lazy(ll i){//标记记得清空
    if(tree[i].ra){
        work_downA(tree[ls],tree[i].ra);
        work_downA(tree[rs],tree[i].ra);
        tree[i].ra=0;
    }
    if(tree[i].rb){
        work_downB(tree[ls],tree[i].rb);
        work_downB(tree[rs],tree[i].rb);
        tree[i].rb=0;
    }
    if(tree[i].rc){
        work_downC(tree[ls],tree[i].rc);
        work_downC(tree[rs],tree[i].rc);
        tree[i].rc=0;
    }
}
//合并非常简单,左右加就行了
void push_up(tre &nowtre,tre ltre,tre rtre){
    nowtre.a=ltre.a+rtre.a;
    nowtre.ab=ltre.ab+rtre.ab;
    nowtre.abc=ltre.abc+rtre.abc;
}
//线段树的修改
void changeA(ll l,ll r,ll i,ll L,ll R){
    if(l>R||r<L)return ;
    if(L<=l&&r<=R){
        tree[i].a=r-l+1;//标记个数就是区间大小
        tree[i].ra=1;
        return ;
    }
    work_lazy(i);
    ll mid=l+r>>1;
    changeA(l,mid,ls,L,R);
    changeA(mid+1,r,rs,L,R);
    push_up(tree[i],tree[ls],tree[rs]);
}
void changeB(ll l,ll r,ll i,ll L,ll R){
    if(l>R||r<L)return ;
    if(L<=l&&r<=R){
        tree[i].ab=tree[i].a;//标记个数就是标记a的个数
        tree[i].rb=1;
        return ;
    }
    work_lazy(i);
    ll mid=l+r>>1;
    changeB(l,mid,ls,L,R);
    changeB(mid+1,r,rs,L,R);
    push_up(tree[i],tree[ls],tree[rs]);
}
void changeC(ll l,ll r,ll i,ll L,ll R){
    if(l>R||r<L)return ;
    if(L<=l&&r<=R){
        tree[i].abc=tree[i].ab;//标记个数就是标记ab的个数
        tree[i].rc=1;
        return ;
    }
    work_lazy(i);
    ll mid=l+r>>1;
    changeC(l,mid,ls,L,R);
    changeC(mid+1,r,rs,L,R);
    push_up(tree[i],tree[ls],tree[rs]);
}

//线段树修改的清空
void ClearA(ll l,ll r,ll i,ll L,ll R){
    if(l>R||r<L)return ;
    if(L<=l&&r<=R){
        tree[i].a=0;
        tree[i].ra=2;
        return ;
    }
    work_lazy(i);
    ll mid=l+r>>1;
    ClearA(l,mid,ls,L,R);
    ClearA(mid+1,r,rs,L,R);
    push_up(tree[i],tree[ls],tree[rs]);
}
void ClearB(ll l,ll r,ll i,ll L,ll R){
    if(l>R||r<L)return ;
    if(L<=l&&r<=R){
        tree[i].ab=0;
        tree[i].rb=2;
        return ;
    }
    work_lazy(i);
    ll mid=l+r>>1;
    ClearB(l,mid,ls,L,R);
    ClearB(mid+1,r,rs,L,R);
    push_up(tree[i],tree[ls],tree[rs]);
}
void ClearC(ll l,ll r,ll i,ll L,ll R){
    if(l>R||r<L)return ;
    if(L<=l&&r<=R){
        tree[i].abc=0;
        tree[i].rc=2;
        return ;
    }
    work_lazy(i);
    ll mid=l+r>>1;
    ClearC(l,mid,ls,L,R);
    ClearC(mid+1,r,rs,L,R);
    push_up(tree[i],tree[ls],tree[rs]);
}

//直接查询答案abc标记的个数
ll query(ll l,ll r,ll i,ll L,ll R){
    if(l>R||r<L)return 0;
    if(L<=l&&r<=R){
        return tree[i].abc;
    }
    work_lazy(i);
    ll mid=l+r>>1;
    return query(l,mid,ls,L,R)+query(mid+1,r,rs,L,R);
}

//其实不用建树，这个是为了清空和初始化
void build(ll l,ll r,ll i){
    tree[i].ra=tree[i].rb=tree[i].rc=0;
    tree[i].a=tree[i].ab=tree[i].abc=0;
    tree[i].l=l;tree[i].r=r;
    if(l==r)return ;
    ll mid=l+r>>1;
    build(l,mid,ls);
    build(mid+1,r,rs);
    push_up(tree[i],tree[ls],tree[rs]);
}

//树刨,轻重链刨分
void dfs1(int u){
    son[u]=-1;
    siz[u]=1;
    for(auto v:mp[u]){
        if(deep[v])continue;
        deep[v]=deep[u]+1;
        fa[v]=u;
        dfs1(v);
        siz[u]+=siz[v];
        if(son[u]==-1||siz[son[u]]<siz[v])son[u]=v;
    }
}
void dfs2(int u,int Top){
    top[u]=Top;
    boc[u]=cnt+siz[u];//这个是当前点子树区间的右端点
    dfn[u]=++cnt;
    rk[cnt]=u;
    if(son[u]==-1)return ;
    dfs2(son[u],Top);
    for(auto v:mp[u]){
        if(v==son[u]||v==fa[u])continue;
        dfs2(v,v);
    }
}

//树链修改,A,B是根到点,C是子树
void updateA(int l,int r){
    int x=top[l],y=top[r];
    while(x!=y){
        if(deep[x]>=deep[y]){
            changeA(1,n,1,dfn[x],dfn[l]);
            l=fa[x]; x=top[l];
        }
        else {
            changeA(1,n,1,dfn[y],dfn[r]);
            r=fa[y]; y=top[r];
        }
    }
    if(dfn[l]<dfn[r]){
        changeA(1,n,1,dfn[l],dfn[r]);
    }
    else {
        changeA(1,n,1,dfn[r],dfn[l]);
    }
}
void updateB(int l,int r){
    int x=top[l],y=top[r];
    while(x!=y){
        if(deep[x]>=deep[y]){
            changeB(1,n,1,dfn[x],dfn[l]);
            l=fa[x]; x=top[l];
        }
        else {
            changeB(1,n,1,dfn[y],dfn[r]);
            r=fa[y]; y=top[r];
        }
    }
    if(dfn[l]<dfn[r]){
        changeB(1,n,1,dfn[l],dfn[r]);
    }
    else {
        changeB(1,n,1,dfn[r],dfn[l]);
    }
}
void updateC(int x){
    changeC(1,n,1,dfn[x],boc[x]);
}

//树链清空,A,B是根到点,C是子树
void clearA(int l,int r){
    int x=top[l],y=top[r];
    while(x!=y){
        if(deep[x]>=deep[y]){
            ClearA(1,n,1,dfn[x],dfn[l]);
            l=fa[x]; x=top[l];
        }
        else {
            ClearA(1,n,1,dfn[y],dfn[r]);
            r=fa[y]; y=top[r];
        }
    }
    if(dfn[l]<dfn[r]){
        ClearA(1,n,1,dfn[l],dfn[r]);
    }
    else {
        ClearA(1,n,1,dfn[r],dfn[l]);
    }
}
void clearB(int l,int r){
    int x=top[l],y=top[r];
    while(x!=y){
        if(deep[x]>=deep[y]){
            ClearB(1,n,1,dfn[x],dfn[l]);
            l=fa[x]; x=top[l];
        }
        else {
            ClearB(1,n,1,dfn[y],dfn[r]);
            r=fa[y]; y=top[r];
        }
    }
    if(dfn[l]<dfn[r]){
        ClearB(1,n,1,dfn[l],dfn[r]);
    }
    else {
        ClearB(1,n,1,dfn[r],dfn[l]);
    }
}
void clearC(int x){
    ClearC(1,n,1,dfn[x],boc[x]);
}


void solve(){
    cin>>n>>m;
    for(int i=2;i<=n;++i){//建树
        int x;cin>>x;
        mp[x].push_back(i);
        mp[i].push_back(x);
    }
    deep[1]=1;//树链刨分
    dfs1(1);
    dfs2(1,1);
    build(1,n,1);//初始化线段树
    while(m--){
        int A,B,C;cin>>A>>B>>C;
        ll ans=0,x;
        for(int i=1;i<=A;++i){
            cin>>Aa[i];
            updateA(Aa[i],1);//根到A集合点打标记
        }
        for(int i=1;i<=B;++i){
            cin>>Bb[i];
            updateB(Bb[i],1);//根到B集合点打标记
        }
        for(int i=1;i<=C;++i){
            cin>>Cc[i];
            updateC(Cc[i]);//C集合子树打标记
        }
        cout<<query(1,n,1,dfn[1],boc[1])<<'\n';//查询整个树的答案
        
        for(int i=1;i<=A;++i){
            clearA(Aa[i],1);//清空根到A集合的标记
        }
        for(int i=1;i<=B;++i){
            clearB(Bb[i],1);//清空根到B集合的标记
        }
        for(int i=1;i<=C;++i){
            clearC(Cc[i]);//清空C集合子树的标记
        }
    }
    for(int i=1;i<=n;++i){//清空和初始化
        mp[i].clear();
        dfn[i]=siz[i]=son[i]=boc[i]=0;
        top[i]=fa[i]=deep[i]=rk[i]=0;
    }
    cnt=0;
}
int main(){
    ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr);
    int _ = 1 ;cin >> _ ;
    while( _-- ){
        solve() ;
    }
    return 0;
}