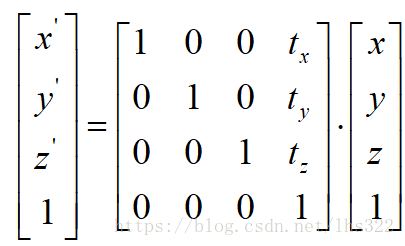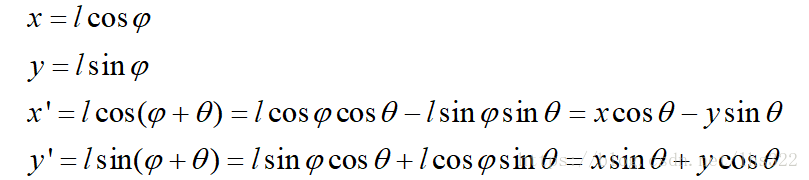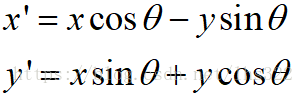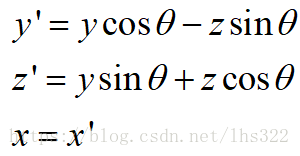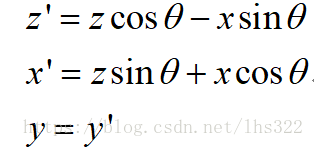博客

三维几何平移与三维坐标轴旋转

三维集合变换的方法是在二维方法的基础上扩充了z坐标而得到。多数情况下，该扩充比较直接，但有一些情况，比如旋转，该扩充就不那么明显。

一个三维位置在齐次坐标中表示为4元列向量。因此，每一次几何变换操作表示为一个从左边去乘坐标向量的4×4矩阵。

1.   三维平移

其矩阵变换形式为：

类似二维坐标变化的实现，我们可以构造一个平移矩阵，如果不懂，请转到

矩阵表示和齐次坐标

：

void Matrix4x4SetIdentity(Matrix4x4 matIdent4x4)  
{  
    //生成一个单位矩阵  
    GLint row, col;  
    for (row = 0; row < 4;++row)  
    for (col = 0; col < 4;++col)  
    {  
        matIdent3x3[row][col] = (row==col);  
    }  
} 
void translate3D(GLfloat tx, GLfloat ty,GLfloat tz)  
{  
    /*通过偏移量tx,ty产生平移矩阵matTransl之后，再通过矩阵的乘法，实现对象的平移*/  
    Matrix3x3 matTransl;//平移矩阵  
    Matrix3x3SetIdentity(matTransl);  
    matTransl[0][3] = tx;  
    matTransl[1][3] = ty;  
matTransl[2][3] = tz;
    /*矩阵乘法，平移*/  
    matrix3x3Premultiply(matTransl,matComposite);  
} 

1.   三维旋转

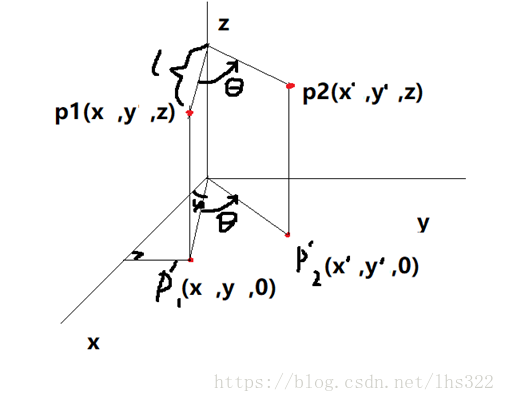
1.1   三维坐标轴旋转

上图为绕z轴的坐标旋转，坐标旋转后x,y轴的坐标位置推导如下：

Z=Z’

矩阵形式：

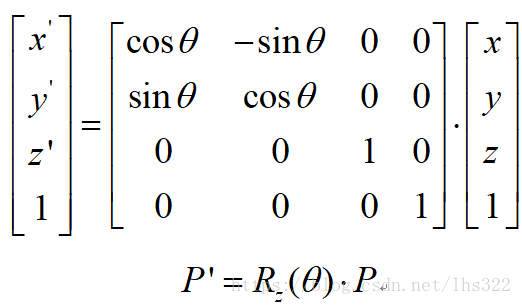
绕另外两个坐标轴的旋转变换公式，可以由

将x、y、z循环替换而得到：

循环替换顺序为：x->y->z->x

因此，为了得到x轴旋转变换，我们用y替代x，z替代y：

为了得到x轴旋转变换，我们用z替代y，x替代z