将同一向量在坐标系1下坐标,转换到坐标系2中,求其坐标,这样的过程叫做坐标变换
假设有1号点和2号点位于世界坐标系中,记世界坐标系为w,点的坐标系为R1和R2,1号点的位姿为
q1 = [0.35,0.2,0.3,0.1],t1 = [0.3,0.1,0.1];二号点的位姿为q2 = [-0.5,0.4,-0.1,0.2],t2 = [-0.1,0.5,0.3];这里的q和t表达的是TRK,w,k = 1,2;也就是世界坐标系到相机坐标系的变换关系。现在,从1号点看到某个点在自身的坐标系下坐标为PR1 = [0.5,0,0.2]的转置,求该向量在二号点坐标系下的坐标
分析如下:
我们已知1号点在自己坐标系下的坐标,要求其在二号坐标系下的坐标。那么思路很明确了,先把已知坐标,转换到世界坐标系下,再把其转换到二号坐标系下,就完成了。那么,关键点也很明确—求变换矩阵。并且要求出两个变换矩阵:
Tw1
一号坐标系到世界坐标系;
T2w
世界坐标系到二号坐标系。那么题目上已经告诉了我们
T1w
和
T2w
(可使用位姿进行转化),我需要将
T1W
转化为
TW1
,那么我们需要求的公式为:
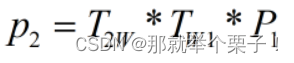
代码和相关注释如下:
#include <iostream>
#include <vector>
#include <algorithm>
#include <Eigen/Core>
#include <Eigen/Geometry>
using namespace std;
using namespace Eigen;
int main(int argc,char **argv )
{
//q1 q2存为两个四元数
Quaterniond q1(0.35,0.2,0.3,0.1), q2(-0.5,0.4,-0.1,0.2);
//四元数进行归一化处理
q1.normalize();
q2.normalize();
//设置两个平移向量 t1 t2
Vector3d t1(0.3,0.1,0.1) , t2(-0.1,0.5,0.3);
//1号点位在自身坐标系下的坐标
Vector3d p1(0.5,0,0.2);
//声明两个变换矩阵,分别代表世界坐标系->1点位 世界坐标系->2点位的坐标变换
Isometry3d T1W(q1),T2W(q2);
//把平移向量赋值给旋转矩阵
//此时的旋转矩阵已经具有平移和旋转的属性
T1W.pretranslate(t1);
T2W.pretranslate(t2);
//p2 = T2W*T1W*P1
Vector3d p2 = T2W*T1W.inverse()*p1;
cout<<"p1-p2转换后的坐标为:"<<p2.transpose()<<endl;
return 0;
}
编译执行即可得转换后的坐标为:
