博客

一个二维数组a[ ][ ]每列的元素的下标规律是 a[ i ][ j ] ，j不变，i 为 0 ~ 行数-1。所以可以一个循环为 0 ~ 列数-1 来表示列下标，内循环一个当前列的每行。

求和的话就是累加就行了。




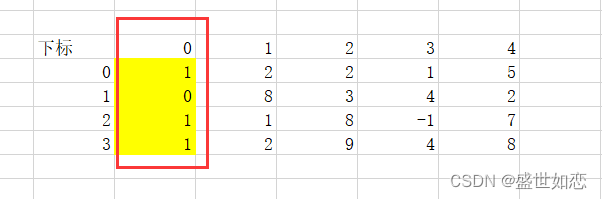
1.每次遍历保存每列最小值的行下标

。如第1列的第3行如果是第1列的最小值，我们用一个变量存下 3 ，即 array[3][1]就是第1列的最小值

#include<iostream>
using namespace std;
int main()
{
	int N = 4;
	int M = 5;
	int array[N][M] = {
		{ 1, 2, 2,1,5},
		{ 0, 8, 3,4,2},
		{ 1, 1, 8,-1,7},
		{ 1, 2, 9,4,8}
	};
	int sum = 0;
	for(int i =0 ; i< M ; i ++){ // 每列 
		int k = 0 ; //表示当前列最小的行下标  array[k][i] 就是表示第i列最小值的位置，初始值为k=0 
		for(int j = 0; j< N ; j++){ // 每行 
			if( array[k][i] > array[j][i] ){  // 有第j行的i列数比第k行的i列更小，更新 k的下标
				k = j;
			}
		}
		// 这个时候的k就是第i列的最小值的行下标。
		cout<<"第"<<i+1<<"列的最小值:"<<array[k][i]<<endl;
		sum += array[k][i];
	}
	cout<< "和为: "<<sum;
	
	
	
}

2.每次遍历用一个数存每列的最小值。

#include<iostream>
using namespace std;
int main()
{
	int N = 4;
	int M = 5;
	int array[N][M] = {
		{ 1, 2, 2,1,5},
		{ 0, 8, 3,4,2},
		{ 1, 1, 8,-1,7},
		{ 1, 2, 9,4,8}
	};
	int sum = 0;
	for(int i =0 ; i< M ; i ++){ // 每列 
		int a_min = array[0][i] ; //表示当前列最小值 
		for(int j = 0; j< N ; j++){ // 每行 
			if( array[j][i] < a_min ){  // 如果第i列的第j行的数比min还小，更新 min的值 
				a_min = array[j][i];
			}
		}
		cout<<"第"<<i+1<<"列的最小值:"<<a_min<<endl;
		sum += a_min;
	}
	cout<< "和为: "<<sum;
	
	
	
}

3.作比较的时候用

#include<algorithm>

中的

min(int a, int b)

函数

。min返回a和b中最小的值。如果不需要保存最小值的当前下标的话可以使用，

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
	int N = 4;
	int M = 5;
	int array[N][M] = {
		{ 1, 2, 2,1,5},
		{ 0, 8, 3,4,2},
		{ 1, 1, 8,-1,7},
		{ 1, 2, 9,4,8}
	};
	int sum = 0;
	for(int i =0 ; i< M ; i ++){ // 每列 
		int a_min = array[0][i] ; //表示当前列最小值 
		for(int j = 0; j< N ; j++){ // 每行 
			a_min = min( array[j][i] , a_min   ); //每次取最小值 
		}
		cout<<"第"<<i+1<<"列的最小值:"<<a_min<<endl;
		sum += a_min;
	}
	cout<< "和为: "<<sum;
	
	
	
}