I. 阅读前你所需的基础知识
-
了解
图 (graph)
的基本知识 (什么是顶点, 什么是边, 什么是路径等等) -
了解图的
深度优先遍历 (DFT, Depth-first Traversal)
-
了解
有向图 (directed graph)
与
无向图 (undirected graph)
II. 连通性(Connectedness)
-
无向图的连通性
-
无向图内的顶点连通性
: 若有一条路径包含顶点A和顶点B,那么顶点A与顶点B互相连通 -
无向图的连通性
:若图像内,
任意
取两个顶点都是互相连通的,那么则称此无向图是连通的 -
连通的无向图示例
:下图是一个具有连通性的无向图,刚接触的人乍一看或许会认为”A和D之间根本就没有连接”,但这时就要注意顶点的连通性了,我们需要的不是A与D,而是存在一条路径,包含A与D,那么这条路径自然是存在的,即为A-B-C-D

-
-
有向图的连通性
-
有向图的连通性
:与无向图不同的,有向图分为
强连通 (strongly connected)
与
弱连通 (weakly connected)
,下面会逐个解释 -
有向图的强连通
:对于图像内
任意
两个顶点A和顶点B,若存在一个
A到B
的路径并存在一个
B到A
的路径,那么称此有向图为强连通 -
强连通有向图示例
:如下图,对于任意两个顶点存在相通的路径, 则此图像为强连通的有向图

-
有向图的弱连通
:若此有向图的无相基础图具有连通性,那么称此有向图为弱连通-
无相基础图 (underlying undirected graph)
:移除一个有向图内所有边的方向性,可以理解为将有向图转变为了无向图
-
-
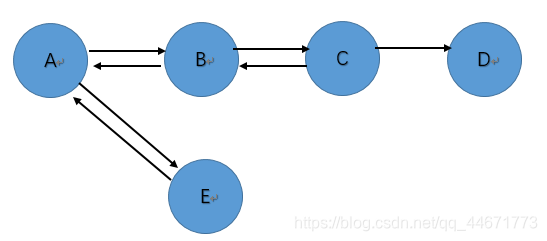
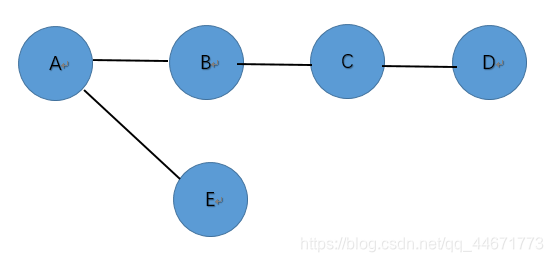
弱连通有向图示例
:注意下面两张图,
第一张
图为
有向图
,
第二张
为其的
无相基础图
。这个图并不是强连通的有向图。我们用顶点A与顶点D为例,图像内存在A到D的路径,为A-B-C-D,但不存在D到A的路径,因为D不存在一个指向C的边。但是,它的无相基础图是连通的,所以此图为弱连通的有向图
-
III. 检测连通性的算法
对于连通性的检测,相对比较便利的方法就是使用深度优先遍历 (DFT) 来访问图内的所有元素,但针对有向图与无向图,我们有不同的检测方式
-
检测无向图是否连通的步骤
:- 将所有顶点标记为未访问
- 通过DFT访问所有顶点,被访问过的顶点标记为已访问
- 检测是否所有顶点都已被访问,若有顶点未被访问,则图不具有连通性
-
伪代码
:
IsUndirectedGraphConnected(UndirectedGraph graph)
{
//将graph内所有顶点标记为未访问
MarkAllVerticeUnvisited(graph)
//任取一个起始顶点,从它开始进行DFT,任何被遍历到的顶点会被标记为已访问
currentVertex = any vertex in graph
DFTMarkVisited(currentVertex)
//检测是否所有顶点都被访问过,并返回结果
return AllVerticeAreVisited(graph)
}
-
检测有向图是否强连通的步骤
:- 将所有顶点标记为未访问
- 通过DFT访问所有顶点,被访问过的顶点标记为已访问
- 检测是否所有顶点都被访问,若有没被访问,则此图不是强连通有向图
- 复制一份当前的有向图
- 在复制的有向图内,将所有顶点标记为未访问
- 在复制的有向图内,把所有的边的方向反转,比如原来A指向B的边,变为B指向A
- 通过DFT访问复制的有向图内所有顶点,被访问过的顶点标记为已访问
- 在复制的有向图内,检测是否所有顶点都被访问,若有没被访问,则此图不是强连通有向图
- 如果第3与第8步均通过,则此图为强连通的有向图
-
为什么要反转边的方向然后再测一次?
:为了证明强连通性,我们必须确保一个点可以“到达所有的点”,还要确保所有的点“可以回到某一个点”,这也是有向图比无向图复杂的地方。-
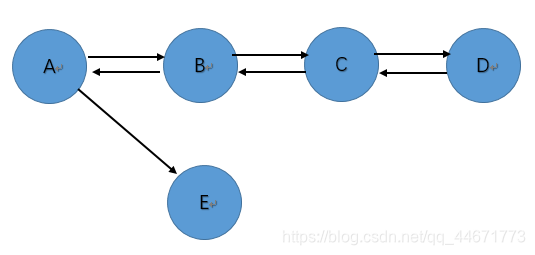
一个简单的示例
: 对于如下的有向图,假设我们以A为起点,只进行到第3步的检测,我们最后得出的结果是”此图是强连通的有向图”。然而我们明显看出,这个图是弱连通,因为E没有指向A的边。很明显,第一步只是证明了“A可以到达其他所有的顶点”,但没有证明“其他所有的顶点也可以到达A”。这时候,如果我们反转所有边的方向再次测试,就会发现A无法到达E,也就是变相说明“E无法到达A”。所以,这个图不是强连通的有向图
-
-
伪代码
:
IsDirectedGraphStronglyConnected(DirectedGraph graph)
{
//将graph内所有顶点标记为未访问
MarkAllVerticeUnvisited(graph)
//任取一个起始顶点,从它开始进行DFT,任何被遍历到的顶点会被标记为已访问
currentVertex = any vertex in graph
DFTMarkVisited(currentVertex)
//检测是否所有顶点都被访问
allvisited = AllVerticeAreVisited(graph)
if allvisited == false:
return false
//复制graph
DirectedGraph copyedGraph = Copy(graph)
//将复制的图内所有顶点标记为未访问
MarkAllVerticeUnvisited(copyedgraph)
//反转所有边的方向
ReverseAllEdges(copyedGraph)
//在复制的图里找到与currentVertex相等的顶点, 并对复制图进行DFT
newCurrentVertex = copyedGraph.FindTheSameVertex(currentVertex)
DFTMarkVisited(newCurrentVertex)
//检测是否所有复制图内的顶点都被访问
allvisited = AllVerticeAreVisited(copyedGraph)
if allvisited == false:
return false
//若以上检测全部通过,则此图为强连通有向图
return true
}
-
检测有向图是否弱连通的步骤
:- 获取当前图的无相基础图
- 检测无相基础图是否具有连通性
- (因为弱连通的验证与基本与验证无向图的连通性相同,所以这里不加伪代码,唯一多的一步就是获取一个有向图的无相基础图)
作者:0 warning
参考资料:我的课堂笔记= =