一、利用奇偶性和区间对称性简化积分计算
解析:注意到积分区域是单位球的上半球,由对称性知关于
的奇函数积分都为
,且
地位相同。
注意是在球体里面积分,
,球面上面才等于!!!
二、变量代换和积分区域的分析和刻画
1.
计算
解析:很容易看出积分区域是一个圆域:
做变换:
变换后雅各比矩阵
于是积分变换为:
注意到积分区域的对称性,关于
的积分为0
2.
试求由六个平面
所围成的平行六面体的体积,其中
解析:做变量代换:
令
则雅各比行列式
分之一
为
于是体积
于是
//这个题注意变量代换后雅各比行列式是
,而题中给的
是
,正好是雅各比矩阵的倒数,故而是乘在
前面。
3.
[习题7-2-8(4)] 求给定曲线所围平面区域的面积。区域是双曲螺线
,圆周
与坐标极轴所围成的较小区域。
解析:在
坐标系下刻划异常困难,我们直接采用极坐标,看
的样子,知道
的积分乘以雅各比行列式就是映射到
坐标系下的积分。
极坐标到直角坐标的雅各比行列式是

由
很容易知道要求积分
4.
求封闭曲线
所围区域的面积。
解析:使用极坐标简化方程。
的极坐标方程为
除去
是一个孤立的奇点外,对应于
平面,区域为:
于是面积
此积分的知识点是:
,
5.
计算
,其中
解析:换元令
所以
于是区域就变成了:
雅各比行列式
所以
6.
求由参数曲线
,以及
所围均匀薄片的质心坐标。
解析:
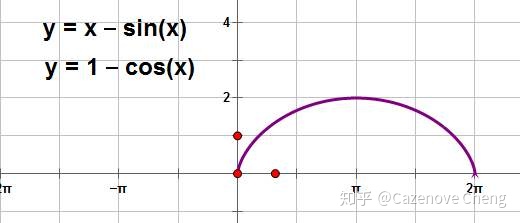
曲线长这样,易知质心横坐标为
,纵坐标计算如下:
积分区域
注意到当
时,
,由此可以确定一个
于是
故而质心坐标
// 一个计算
正解:
错解:
自己思考为什么不能这样解。
Updating…