链接：https://ac.nowcoder.com/acm/contest/11233/A

来源：牛客网

A-平行四边形

题目描述:

给出四个点，判断是否构成不退化的平行四边形。（退化指存在三点共线）

输入描述:

本题有多组数据，第一行是数据组数 T。

每组数据输入四行，每行两个整数，分别为x1,y1,x2,y2,x3,y3,x4,y4,描述四个点的坐标(x1,y1),(x2,y2),(x3,y3),(x4,y4)

输出描述:

对每组数据输出一行一个字符串 YES 或者 NO（全部大写），分别表示是或不是平行四边形。

输入:

4
0 0 
1 1 
0 1 
1 0
0 1 
1 1 
1 0 
0 0
0 0 
1 1 
2 2 
3 3
4 2 
5 3 
6 6 
9 -10

输出:

YES
YES
NO
NO

说明:

样例的第 1,2 组数据中的点组成了正方形，自然是平行四边形。

第三组数据四个点共线，不是平行四边形。最后一组数据四个点不组成平行四边形。

备注:

对于 50% 的数据，不存在三点共线。

对于 100%的数据，1≤T≤10 ^ 4，∣xi∣∣yi∣ ≤ 10 ^ 9。

题解

我们都知道

平行于X轴的直线的斜率为零，平行于Y轴的直线的斜率不存在。

而对于过两个已知点(x1，y1)和(x2，y2)的直线，若x1≠x2，则该直线的斜率为k=(y1-y2)/(x1-x2)。

根据平行四边形的判定条件：

两组对边分别平行的四边形是平行四边形

所以判断

（x1，y1）（x2，y2）两点之间的斜率是否与（x3，y3）（x4，y4）之间的斜率相等

（x1，y1）（x3，y3）两点之间的斜率是否与（x2，y2）（x4，y4）之间的斜率相等

（x1，y1）（x4，y4）两点之间的斜率是否与（x2，y2）（x3，y3）之间的斜率相等

这3个条件，只要有两种条件成立（即1,2或者1,3），则该四边形是平行四边形

坐标的两种情况（如图）

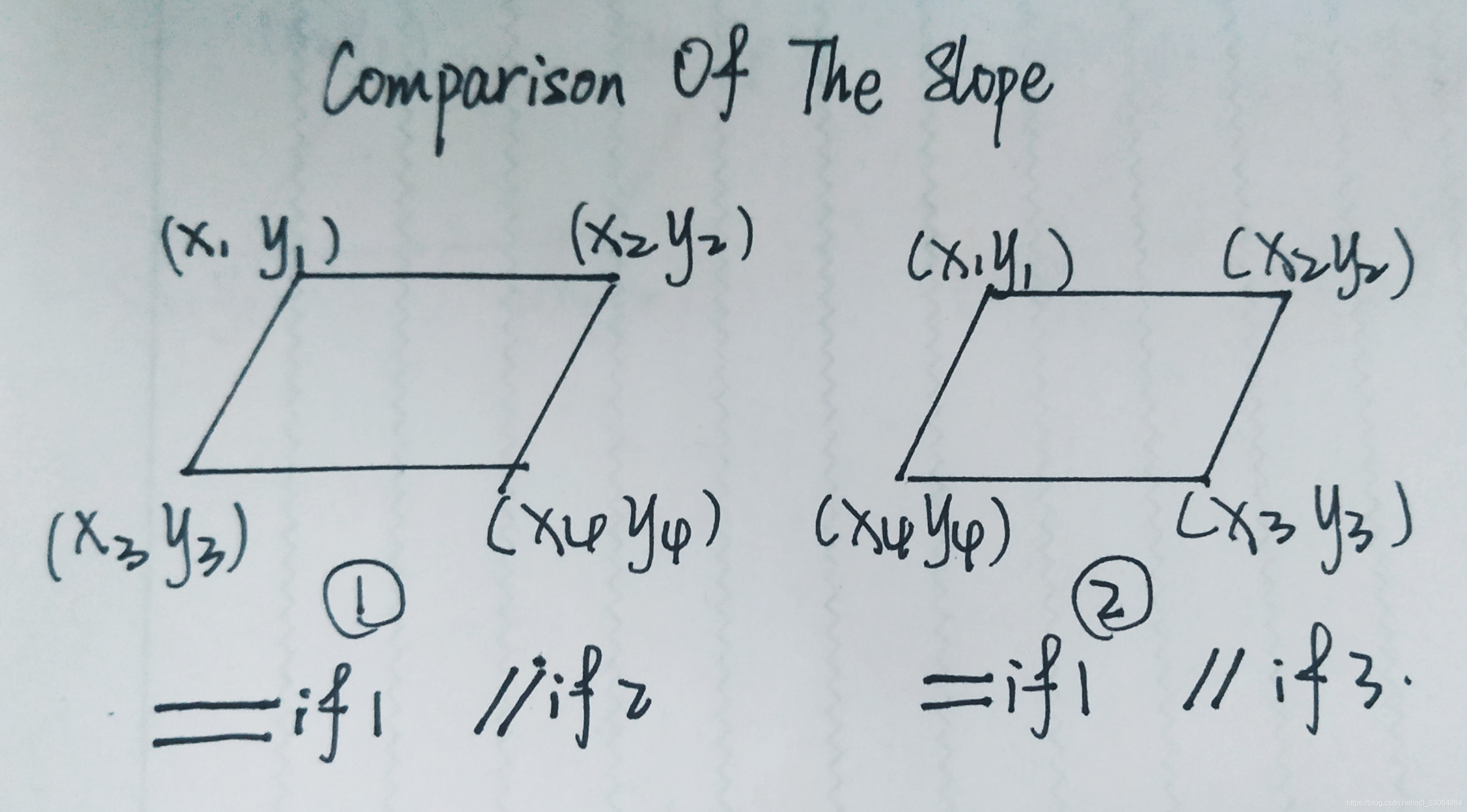
代码:

#include <iostream>
using namespace std;
int x1,y1,x2,y2,x3,y3,x4,y4;
bool ComparisonOfTheSlope()
{
    int count=0;
    if((y1-y2)*(x3-x4)==(y3-y4)*(x1-x2))
        count++;
    if((y1-y3)*(x2-x4)==(y2-y4)*(x1-x3))
        count++;
    if((y1-y4)*(x2-x3)==(y2-y3)*(x1-x4))
        count++;
    if(count==2)
        return 1;//该四边形是平行四边形
    else
        return 0;//该四边形不是平行四边形
}
int main()
{
    int T;
    cin>>T;
    for(int i=1;i<=T;i++)
    {
        cin>>x1>>y1>>x2>>y2>>x3>>y3>>x4>>y4;
        if(ComparisonOfTheSlope())
            cout<<"YES"<<endl;
        else
            cout<<"NO"<<endl;
    }
    return 0;
}