一、线性Attention的探索:Attention必须有个Softmax吗?

前几天笔者读到了论文 Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention [1] ,了解到了线性化 Attention (Linear Attention)这个探索点,继而阅读了一些相关文献,有一些不错的收获,最后将自己对线性化 Attention 的理解汇总在此文中.
Attention

相关解读可以参考笔者的一文读懂「Attention is All You Need」| 附代码实现,以及它的一些改进工作也可以参考突破瓶颈,打造更强大的 Transformer [3]、Google 新作 Synthesizer:我们还不够了解自注意力,这里就不多深入介绍了。
1.1 摘掉Softmax
读者也许想不到,制约 Attention 性能的关键因素,其实是定义里边的 Softmax!事实上,简单地推导一下就可以得到这个结论。

注:关于矩阵乘法算法复杂度的计算
1).矩阵乘法
对于矩阵A(n×m),B(m×n), 这里A(n×m)表示A是n行乘m列的矩阵。
如果A×B,那么复杂度为O(n×m×n),即O(n^2×m) 。进一步思考,为什么呢,直接代码解释:
for(i=0;i<n;i++){ //A矩阵中的n
for(j=0;j<m;j++){ //A矩阵中的m 或者B矩阵中的m ,一样的
for(k=0;k<n;k++){ //B矩阵中的n
C[i][j]= C[i][j]+A[i][k]*B[k][j];
}
}
}
一个for循环是O(n),这里是三个for循环,所以为O(n×m×n)。(ps:个人感觉还是看代码比较好理解,后面三个矩阵乘法时,就会更加体会到)
对于矩阵A(m×n),B(n×m)和C(m×n), 这里A(m×n)表示A是m行乘n列的矩阵。(PS:这里记号和前面不同,主要方便和知乎截图符号一致)
- A×B,那么复杂度为O(m×n×m),即O(m^2×n) 。
- D(m×m)=A×B运算完后在和C运算。
-
D×C,那么复杂度为O(m×m×n),即O(m^2×n) 。

为了方面理解,笔者直接上代码,这样清楚一点。
int A(m*n),
int B(n*m)
int C(m*n)
int D(m*m)
int E(m*n)
//先计算D=A*B
for(i=0;i<m;i++){ //A矩阵中的m
for(j=0;j<n;j++){ //A矩阵中的n 或者B矩阵中的n ,一样的
for(k=0;k<m;k++){ //B矩阵中的m
D[i][j]= D[i][j]+A[i][k]*B[k][j];
}
}
}
//在计算E=D*C
for(i=0;i<m;i++){ //D矩阵中的m
for(j=0;j<m;j++){ //D矩阵中的m 或者C矩阵中的m ,一样的
for(k=0;k<n;k++){ //C矩阵中的n
E[i][j]= E[i][j]+A[i][k]*B[k][j];
}
}
}

1.2 一般的定义
问题是,
直接去掉 Softmax 还能算是 Attention 吗?它还能有标准的 Attention 的效果吗?
为了回答这个问题,我们先将 Scaled-Dot Attention 的定义(1)等价地改写为(本文的向量都是列向量)。
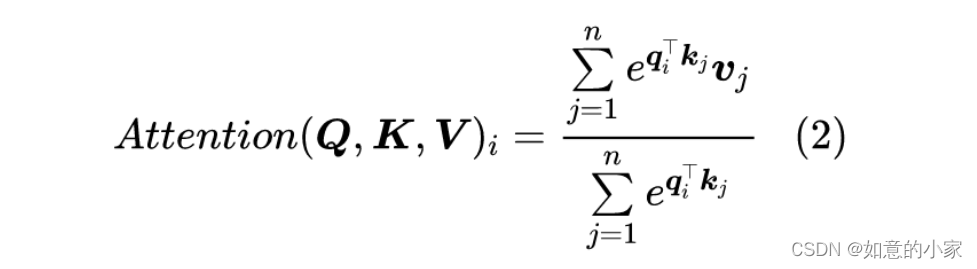


补充:
下面给出了sfoftmax的相关定义(以第i个节点输出为例):

引入指数函数对于Softmax函数是把双刃剑,即得到了优点也暴露出了缺点:
-
引入指数形式的优点

import tensorflow as tf
print(tf.__version__) # 2.0.0
a = tf.constant([2, 3, 5], dtype = tf.float32)
b1 = a / tf.reduce_sum(a) # 不使用指数
print(b1) # tf.Tensor([0.2 0.3 0.5], shape=(3,), dtype=float32)
b2 = tf.nn.softmax(a) # 使用指数的Softmax
print(b2) # tf.Tensor([0.04201007 0.11419519 0.8437947 ], shape=(3,), dtype=float32)
两种计算方式的输出结果分别是:
tf.Tensor([0.2 0.3 0.5], shape=(3,), dtype=float32)
tf.Tensor([0.04201007 0.11419519 0.8437947 ], shape=(3,), dtype=float32)
结果还是挺明显的,经过
使用指数形式的Softmax函数能够将差距大的数值距离拉的更大
。

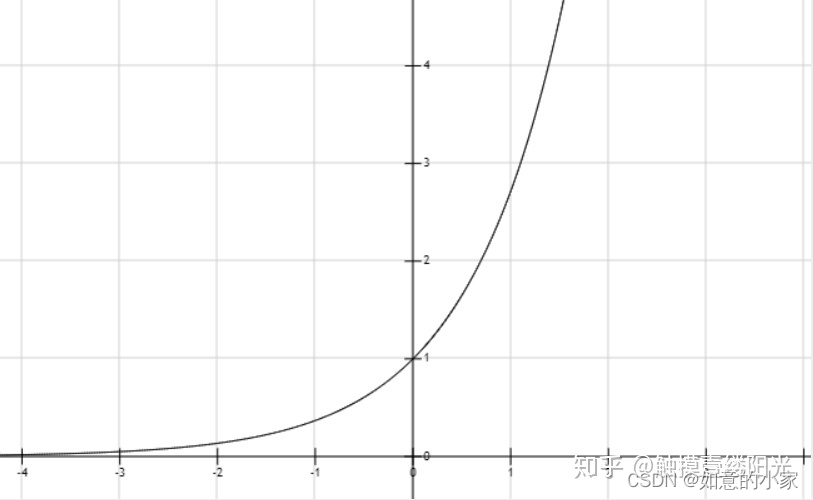
2. 引入指数形式的缺点
指数函数的曲线斜率逐渐增大虽然能够将输出值拉开距离,但是也带来了缺点,当 值非常大的话,计算得到的数值也会变的非常大,
数值可能会溢出
。
import numpy as np
scores = np.array([123, 456, 789])
softmax = np.exp(scores) / np.sum(np.exp(scores))
print(softmax) # [ 0. 0. nan]
当然针对数值溢出有其对应的优化方法,将每一个输出值减去输出值中最大的值。
import numpy as np
scores = np.array([123, 456, 789])
scores -= np.max(scores)
p = np.exp(scores) / np.sum(np.exp(scores))
print(p) # [5.75274406e-290 2.39848787e-145 1.00000000e+000]
几个例子
值得指出的是,下面
介绍的这几种 Linear Attention
,前两种只做了 CV 的实验,第三种是笔者自己构思的,所以都还没有在 NLP 任务上做过什么实验,各位做模型改进的 NLPer 们就有实验方向了。
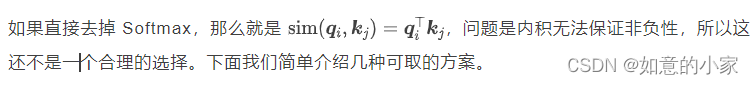
2.1 核函数形式

注:里面的核函数是如何进行相关联的推导的呢?
2.2 妙用Softmax

如何证明这是一个特例呢?
相关工作
通过修改 Attention 的形式来降低它的计算复杂度,相关的工作有很多,这里简要列举一些。
3.1 稀疏Attention
我们之前介绍过 OpenAI 的 Sparse Attention,通过“
只保留小区域内的数值、强制让大部分注意力为零”的方式
,来减少 Attention 的计算量。经过特殊设计之后,Attention 矩阵的非 0 元素只有O(n) 个,所以理论上它也是一种线性级别的 Attention。
类似的工作还有 Longformer。
但是很明显,
这种思路有两个不足之处:
- 如何选择要保留的注意力区域,这是人工主观决定的,带有很大的不智能性;
- 它需要从编程上进行特定的设计优化,才能得到一个高效的实现,所以它不容易推广。
3.2 Reformer
Reformer 也是有代表性的改进工作,它将 Attention 的复杂度降到了O(nlogn) 。
某种意义上来说,
Reformer 也是稀疏 Attention 的一种
,只不过它的稀疏 pattern 不是事先指定的,而是
通过 LSH(Locality Sensitive Hashing)技术(近似地)快速地找到最大的若干个 Attention 值,然后只去计算那若干个值
。
此外,Reformer 通过构造
可逆形式
的 FFN(Feedforward Network)替换掉原来的 FFN,然后
重新设计反向传播过程
,从而
降低了显存占用量
。
所以,相比前述稀疏 Attention,
Reformer 解决了它的第一个缺点,但是依然有第二个缺点:实现起来复杂度高
。要实现 LSH 形式的 Attention 比标准的 Attention 复杂多了,对可逆网络重写反向传播过程对普通读者来说更是遥不可及。
3.3 Linformer
跟本文所介绍的 Linear Attention 很相似的一个工作是 Facebook 最近放出来的 Linformer,它依然保留原始的 Scaled-Dot Attention 形式,但在进行 Attention 之前,用两个m×n 的矩阵E、F 分别对 K、V进行投影,即变为

但是,笔者认为
“对于超长序列 m 可以保持不变”这个结论是值得质疑的
,原论文中对于长序列作者只做了 MLM 任务,而很明显 MLM 并不那么需要长程依赖,所以这个实验没什么说服力。因此,Linformer 是不是真的 Linear,还有待商榷。
3.4 自回归生成
Linformer 的另一个缺点是EK、FV 这两变直接把整个序列的信息给“糅合”起来了,所以它没法简单地把将来信息给 Mask 掉(Causal Masking),从而无法做语言模型、Seq2Seq 等自回归生成任务
,这也是刚才说的原作者只做了 MLM 任务的原因。

第二种方法该怎么进行相关的理解呢?
3.5 下采样技术

注:
将原本的n×n序列变为了n×m,相当于进行了相关的下采样操作,非常的便捷。
还有一些其他的下采样方法,如采用不同的步长来进行相应的处理。
3.6 总结
本文介绍了一些从结构上对 Attention 进行修改从而降低其计算复杂度的工作,其中
最主要的 idea 是去掉标准 Attention 中的 Softmax,就可以使得 Attention 的复杂度退化为理想的 O(n) 级别(Linear Attention)。
相比于其他类似的改进结构的工作,这种修改能在把复杂度降到 O(n) 的同时,依然保留所有的 “token-token” 的注意力,同时还能保留用于做自回归生成的可能性。
二、Performer:用随机投影将Attention的复杂度线性化
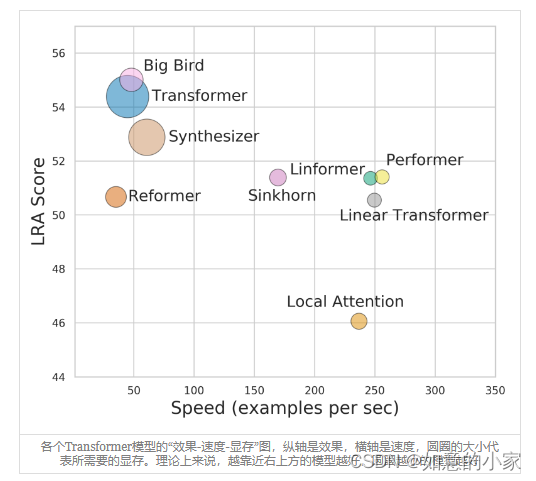
Attention 机制的 复杂度O(n^2)是一个老大难问题了,改变这一复杂度的思路主要有两种:一是走稀疏化的思路
,比如我们以往介绍过的 Sparse Attention 以及 Google 前几个月搞出来的 Big Bird [1] ,等等;
二是走线性化的思路
,这部分工作我们之前总结在线性 Attention 的探索:Attention 必须有个 Softmax 吗?中,读者可以翻看一下。
本文则介绍一项新的改进工作 Performer,出自 Google 的文章 Rethinking Attention with Performers,它的目标相当霸气:
通过随机投影,在不损失精度的情况下,将 Attention 的复杂度线性化
。
说直接点,就是理想情况下我们可以
不用重新训练模型,输出结果也不会有明显变化,但是复杂度降到了O(n)
!看起来真的是“天上掉馅饼”般的改进了,真的有这么美好吗?

三、简单回顾
如果读者对线性 Attention 还不是很了解,那么建议先通读一下
线性 Attention 的探索:Attention 必须有个 Softmax 吗?
和
Performer:用随机投影将 Attention 的复杂度线性化
。总的来说,
线性 Attention 是通过矩阵乘法的结合律来降低 Attention 的复杂度
。
3.1 标准Attention

3.2 线性Attention
注意:
sim(q,k)如果去掉了softmax函数的话,则可直接表示为q,k,为了保证非负,所以每个q,k均使用相应的二激活函数来进行相应的处理。

3.3 Performer

如何将低维空间中两个向量的核函数映射为高维空间中两个向量的内积。
由图可知:
看起来Performer是挺不错的,那是不是说我们就可以用它来替代Transformer了?并不是,纵然Performer有诸多可取之处,但仍然存在一些无法解决的问题。
首先,为了更好地近似标准Transformer,Performer的m必须取得比较大,至少是m>d,一般是d的几倍,这也就是说,Performer的head_size要比标准Transformer要明显大。虽然理论上来说,不管m多大,只要它固定了,那么Performer关于序列长度的复杂度是线性的,但是m变大了,在序列长度比较短时计算量是明显增加的。换句话说,短序列用Performer性能应该是下降的,根据笔者的估计,
只有序列长度在5000以上,Performer才会有比较明显的优势
。
其次,目前看
来Performer(包括其他的线性Attention)跟相对位置编码是不兼容的,因为相对位置编码是直接加在Attention矩阵里边的,Performer连Attention矩阵都没有,自然是加不了的
。此外,像UniLM这种特殊的Seq2Seq做法也做不到了,不过普通的单向语言模型还是可以做到的。总之,O(n2)的Attention矩阵实际上也带来了很大的灵活性,而线性Attention放弃了这个Attention矩阵,也就放弃了这种灵活性了。
最后,也是笔者觉得最大的问题,就是Performer的思想是将标准的Attention线性化,所以为什么不干脆直接训练一个线性Attention模型,而是要向标准Attention靠齐呢?从前面的最后一张图来看,Performer并没有比Linear Transformer有大的优势(而且笔者觉得最后一张图的比较可能有问题,Performer效果可能比Linear Transformer要好,但是速度怎么可能还超过了Linear Transformer?Performer也是转化为Linear Transformer的,多了转化这一步,速度怎能更快?),因此Performer的价值就要打上个问号了,毕竟线性Attention的实现容易得多,而且是通用于长序列/短序列,Performer实现起来则麻烦得多,只适用于长序列。
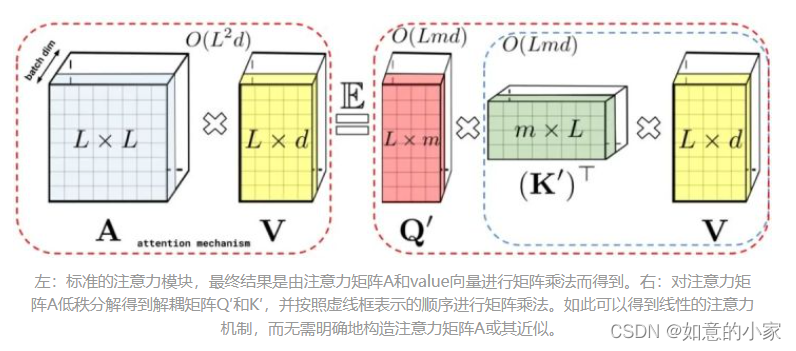
通过上述的分解可以得到线性(而非二次)空间复杂度隐式注意力矩阵。同样,通过分解可以获得线性时间的注意力机制。原有的方式是注意力矩阵与value输入相乘得到最终结果,但在
分解注意力矩阵
之后,可以重新排列矩阵乘法来近似常规注意力机制的结果,而无需显式地构建二次方尺寸的注意力矩阵。最终生成了新算法 FAVOR+。
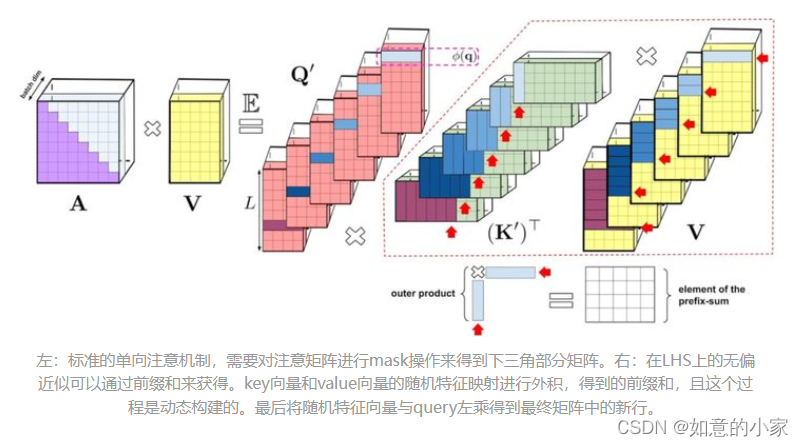
上述分析是双向注意力(即非因果注意力),并没有区分 past 和 future的部分。那么如何做到让输入序列中只注意到其中一部分,即单向的因果注意力?只需使用前缀和计算(prefix-sum computation),在计算过程只存储矩阵计算的运行总数,而不存储完整的下三角常规注意力矩阵。
四、Nyströmformer
在这部分内容中,我们以一个
简单的双重 softmax 形式的线性 Attention 为出发点,逐步寻找更加接近标准 Attention 的线性 Attention
,从而得到 Nyströmformer。
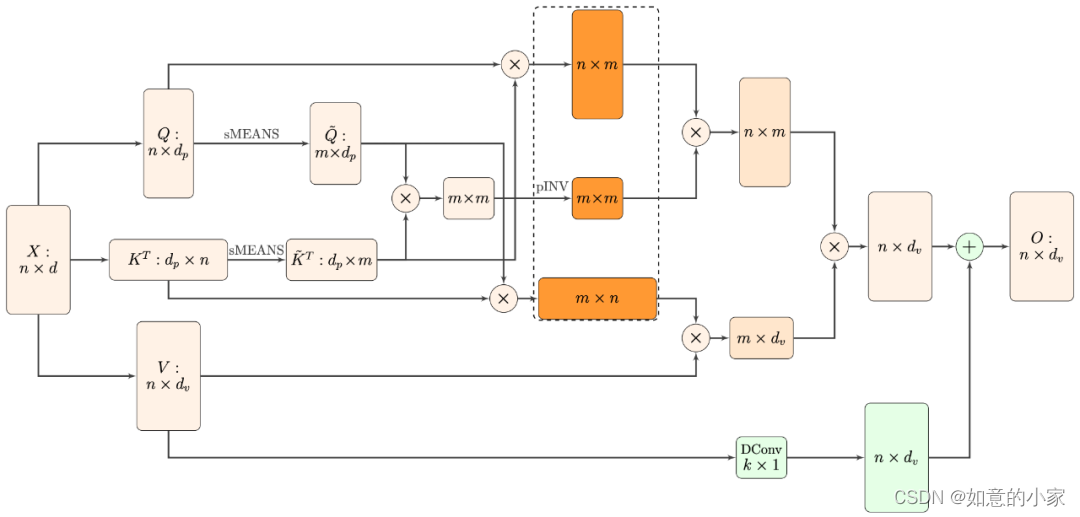
▲ Nyströmformer结构示意图。读者可以读完下面几节后再来对照着理解这个图。
4.1 双重Softmax
在文章线性 Attention 的探索:Attention 必须有个 Softmax 吗?中我们提到了一种比较有意思的线性 Attention,它使用了双重 softmax 来构建 Attention 矩阵:
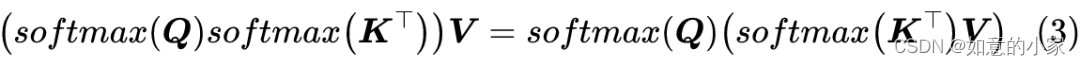
可以证明这样
构造出来的 Attention 矩阵自动满足归一化要求,不得不说这是一种简单漂亮的线性 Attention 方案
。

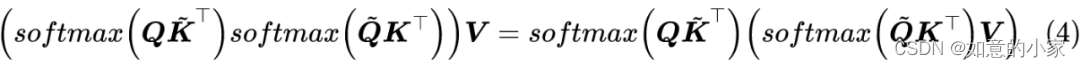
具体的聚类过程我们稍后再来讨论。现在,
softmax 的对象是内积的结果,具有比较鲜明的物理意义
,因此可以认为上式比前面的式 (3) 更为合理。
如果我们选定一个比较小的 m,那么上式右端的复杂度只是线性地依赖于 n,因此它也是一个线性 Attention
。
4.2 向标准靠近
纯粹从改进式 (3) 的角度来看,式 (4) 已经达到目标了,不过 Nyströmformer 并不局限于此,它还希望
改进后的结果与标准 Attention 更加接近
.
为此,观察到式 (4) 的
注意力矩阵 是一个n×m 的矩阵乘以一个m×n 的矩阵
,为了微调结果,又不至于增加过多的复杂度,我们可以考虑在中间插入一个 M 的矩阵 :

作为 Attention 矩阵,它是三个小矩阵的乘积,因此通过矩阵乘法的结合律就能转化为线性 Attention。
下面介绍的是如何来求所加入的M矩阵的逆矩阵以及什么情况下它是不可逆的?(行列式严格等于0)
当矩阵可逆时,矩阵的伪逆和逆矩阵是相等的。

如何对矩阵求伪逆矩阵?
2.3 迭代求逆阵


2.4 池化当聚类

2.5 性能与效果
可能受限于算力,原论文做的实验不算特别丰富,主要是将 small 和 base 版本的 BERT 里边的标准 Attention 替换为 Nyströmformer 进行对比实验,实验结果主要是下面两个图。
其中一个是预训练效果图,其中比较有意思的是
Nyströmformer 在 MLM 任务上的效果比标准 Attention 还要优;另外是在下游任务上的微调效果,显示出跟标准 Attention(即 BERT)比还是有竞争力的。
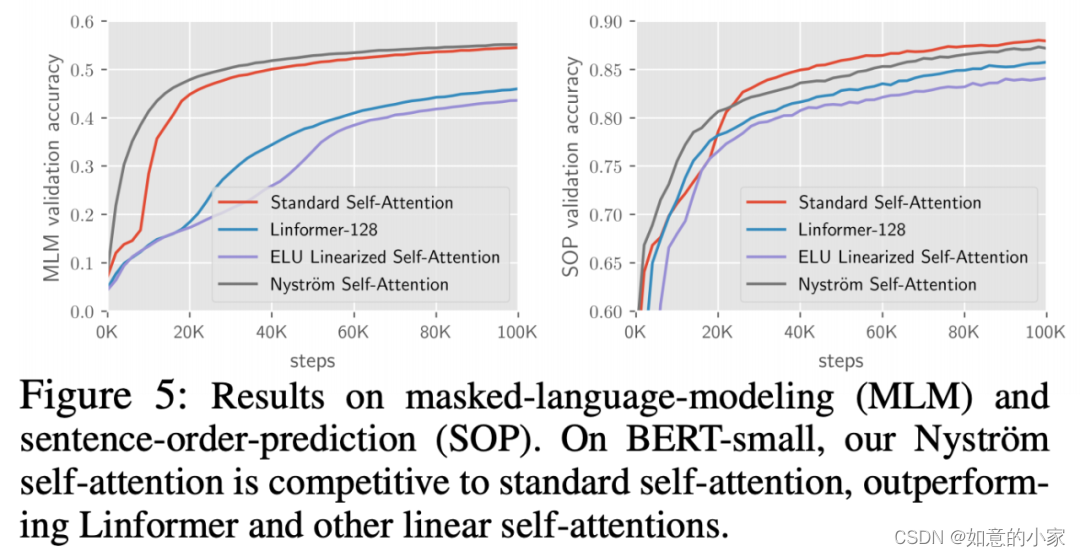
Nyströmformer在预训练任务(MLM和SOP)上的效果
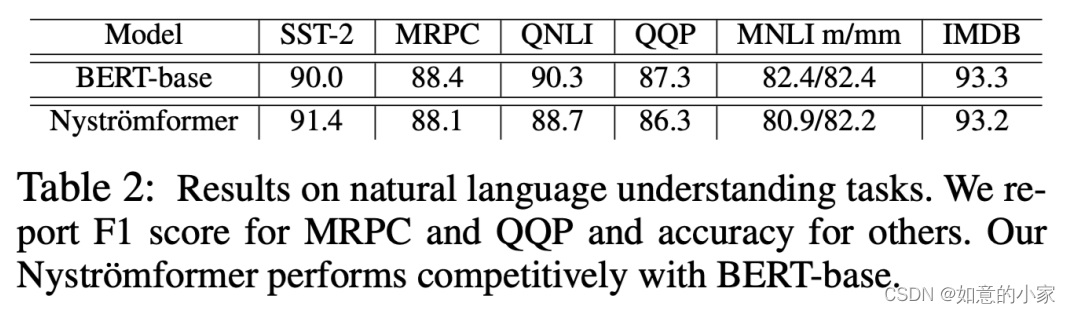
Nyströmformer在下游任务的微调效果
不过,原论文并没有比较 Nyströmformer 跟同类模型的效果差异,只是提供下面的一张复杂度对比图,因此无法更好地突出 Nyströmformer 的竞争力:

不同模型的时间和空间复杂度对比图
2.6 个人思考
总的来说,Nyströmformer 对标准 Attention 进行近似线性化的思路还是比较新颖的,值得学习与参考。不过伪逆部分的处理总感觉有点不大自然,这部分可能是未来的一个改进点,如果可以做到不用近似,那就比较完美了。还有,如何定量地估计 Nyströmformer 与标准 Attention 的误差,也是一个值得思考的理论问题。
从实验上来看,Nyströmformer 跟标准 Attention 相比还是显得有竞争力的,尤其是 MLM 的结果比标准 Attention 还好,显示了 Nyströmformer 的潜力。此外,前面说到包含了 Pooling 导致不能做自回归生成是 Nyströmformer 的一个显著缺点,不知道有没有办法可以弥补,反正笔者目前是没有想到好的方向。
跟 Performer 相比,Nyströmformer 去除了线性化过程中的随机性,因为 Performer 是通过随机投影来达到线性化的,这必然会带来随机性,对于某些有强迫症的读者来说,这个随机性可能是难以接受的存在,而 Nyströmformer 则不存在这种随机性,因此也算是一个亮点。
2.7 Nyström方法

小结:
本文介绍了提升 Transformer 效率的一个新工作 Nyströmformer,它借鉴了 Nyström 方法的思想来构建一个能逼近标准 Attention 的线性 Attention,类似思想的工作还有 Performer,两者相比各有自己的优缺点,都是值得学习的工作。