在
数学
与
物理学
中,
相空间
是一个用以表示出一系统所有可能状态的空间;系统每个可能的状态都有一相对应的相空间的点。
相空间是一个
六维
假想空间,其中动量和空间各占
三维
。每个相格投影到px-x平面上后面积总是h。尽管相格的形状如图所示可能十分任意,但我们可以把它们想象为方的或长方的。
一个随时间演化的system, 我们可以描述出它的运动轨迹, 以及它在运动轨迹上任一点的速度, 这样它的演化过程就被完全描述. 所以, 我们可以用它在每个时刻的position和velocity来描述它在任一时刻的state. 在 classical mechanics当中, 我们认为一个system在某一时刻的position和momentum 也是是唯一确定的, 因此, 这个system随时间演化的过程中所处的每一个state 也可以由系统的position和momentum来描述. 假定有一个在三维空间中运动的粒子, 它在任意一个时刻都有三个coordinates x , y, z以及三个momentum components px, py, pz, 所以我们要描述这个单粒子在某一时刻的运动状态, 就需要6个分量. 按照惯例, 我们将位置坐标记为q, 动量坐标记为p, 这个pq空间就称作phase space. 显然这个相空间是一个六维的空间, 其中动量分量和坐标分量各占三维. 如果一个系统处在三维空间, 这个系统包含N个粒子, 那么我们为了在phase space中描述这个系统, 就需要一个6N维的phase space. Phase space 中的每一个点就表示系统的一个state.
下面, 我们看两个例子.
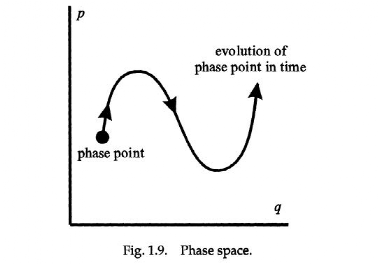
下图所示为一个单粒子在一维空间(一条线)上的运动情形, 它随时间的演化情况在phase space 中被描述为一条在pq组成的一个平面上的运动轨迹.
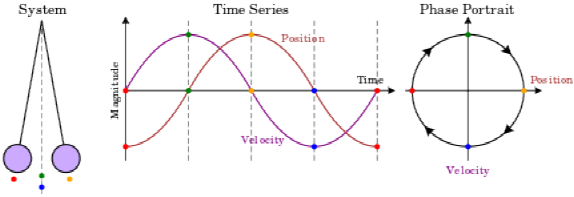
单摆的运动情况(图片来自Wikipedia)
我们为什么要用位置和动量来描述系统的状态, 这是为了使我们的研究方法更一般化更简单化. 实际上我们在用相空间描述系统的状态时, 我们不只是可以用位置和动量, 而是可以用广义坐标和对应的广义动量, 这样我们所能处理的问题就更普遍. 另外, 我们在研究力学问题时, 总是会去考虑系统的Lagrangian 和Hamiltonian, 我们选取了广义坐标和广义动量的描述方式, 就使得问题的研究变得可能或者更简单.
下面再来谈谈phase space 的一个性质——相空间中代表点的轨迹不相交
简单来说, 就是因为在经典力学一个系统的演化是确定的, 所以每一个时刻系统内任意一个粒子的位置和动量是确定的. 从物理上看, 如果在相空间中存在轨迹交叉的情况, 那么假设系统的初态在交叉点, 这样有可能存在两种演化轨迹, 这与演化的确定性相违背.(谁有好的严格的数学推理, 欢迎补充讨论)
从相空间轨迹不交叉这一结论出发, 可以很容易得到经典力学中的一个重要结论: 相流不可压缩, 即 Liouville 定理.