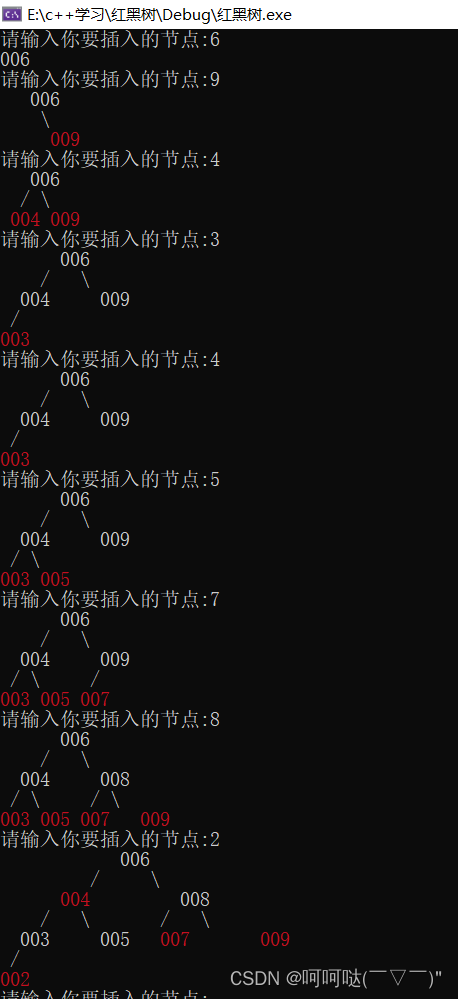
我录制的讲解视频放在B站(以下是链接,大家可以根据这个博客和视频来学习):
从2-3-4树到红黑树原理分析以及C++实现红黑树建树_哔哩哔哩_bilibili







总结规律:
1、2-3-4树:新增元素+2节点合并(节点中只有1个元素)=3节点(节点中有2个元素)
红黑树:新增一个红色节点+黑色父亲节点=上黑下红(2节点—————不要调整)
2、2-3-4树:新增元素+3节点合并(节点中有2个元素)=4节点(节点中有3个元素)
这里有6种小情况(左3,右3,还有2个左中右不需要调整)——
左3,右3需要调整
,其余2个不需要调整
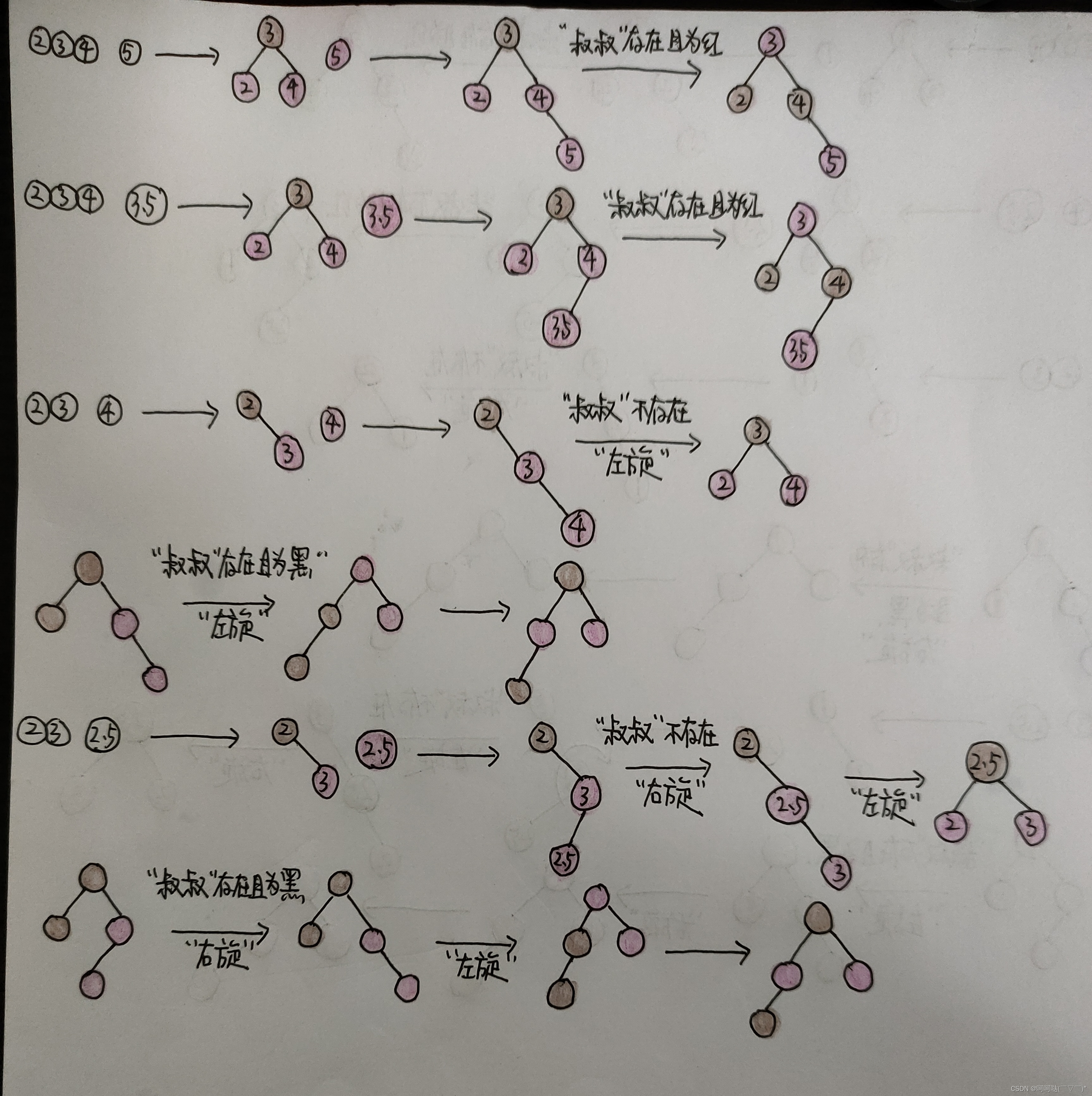
左3,右3(叔叔结点不存在):
还有2个左中右不需要调整
红黑树:新增红色节点+上黑下红=排序后中间节点是黑色,两边节点都是红色(3节点)
注意:叔叔结点存在且为黑 且为左3或者右3结构
也需要进行调整
(后面会总结讲到)
3、2-3-4树:新增一个元素+4节点合并=原来的4节点分裂,中间元素升级为父节点,新增元素与剩下的其中一个合并
(叔叔结点存在且为红,
需要进行调整
)
红黑树:新增红色节点+爷爷节点黑,父节点和叔叔节点都是红色=爷爷节点变红,父亲和叔叔变黑,如果爷爷是根节点,则再变黑
>>由以上的2-3-4树分析可得出需要调整的情况如下:
(一)左三(结点插在祖父节点的左子树)
1、“叔叔存在且为红”的时候,只需要进行颜色调整+继续向上调整
2、若新增结点挂在父结点的左子树(前提),出现”叔叔不存在”或者“叔叔存在且为黑”,两种情况统一操作:先进行一次“右旋”,再进行“颜色调整
3、若新增结点挂在父结点的右子树(前提),出现”叔叔不存在”或者“叔叔存在且为黑”,两种情况统一操作:先进行两次“旋转”,先“左旋”后“右旋”,再进行“颜色调整”
(二)右三(结点插在祖父节点的右子树)
1、“叔叔存在且为红”的时候,只需要进行颜色调整+继续向上调整
2、若新增结点挂在父结点的右子树(前提),出现”叔叔不存在”或者“叔叔存在且为黑”,两种情况统一操作:先进行一次“左旋”,再进行“颜色调整”
3、若新增结点挂在父结点的左子树(前提),出现”叔叔不存在”或者“叔叔存在且为黑”,两种情况统一操作:先进行两次“旋转”,先“右旋”后“左旋”,再进行“颜色调整”
>>这些情况后文会详解分析并给出核心代码
分左3,右3情况讨论:
何为调整?(颜色调整+旋转调整)
(一)左三(结点插在祖父节点的左子树)
1、
“叔叔存在且为红”
的时候,只需要进行
颜色调整+继续向上调整
,即把
父亲结点和叔叔结点的颜色设置为
BLACK
,
把祖父结点的颜色设置为
RED
(若祖父结点为根结点,则再变黑);

讨论可能出现的问题,新增结点加入之后,经过变色调整后,还需要继续向上调整
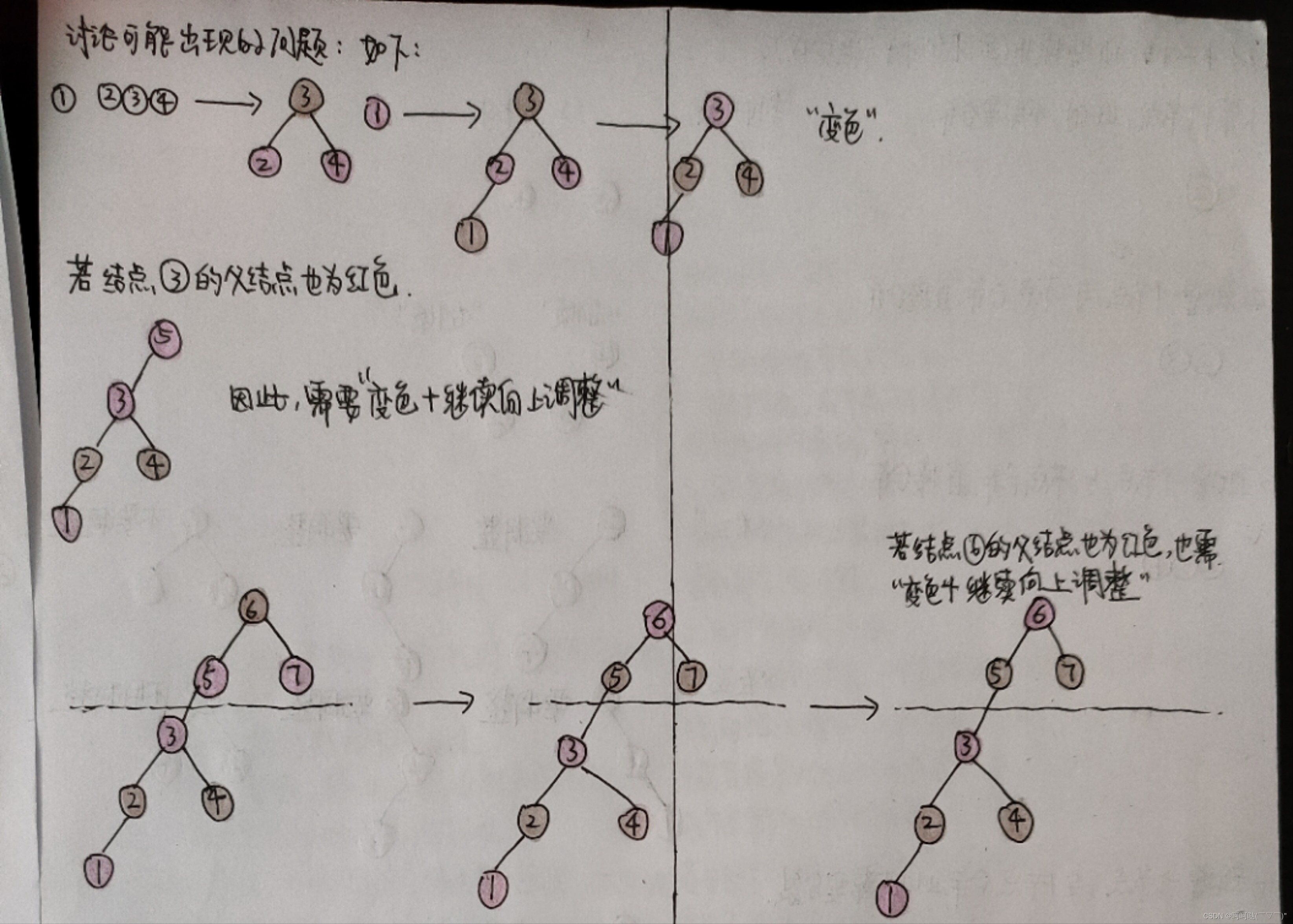
部分核心代码:
//1、uncle存在且为红 if (uncle && uncle->color == RED) { /* 变色 + 继续向上处理 */ //①变色 p->color = uncle->color = BLACK; grandfather->color = RED; //②继续向上处理 cur = grandfather; p = cur->parent; }
2、
若新增结点挂在父结点的左子树
(前提),出现”叔叔不存在”
或者
“叔叔存在且为黑”
,两种情况统一操作:
先进行一次“右旋”,再进行“颜色调整”
,
把父结点颜色设置为
BLACK
,把祖父结点的颜色设置为
RED

部分核心代码:
//2、若新增结点挂在父结点的左子树(前提),uncle不存在/存在且为黑进行统一调整 if (cur == p->left) { //单旋 rightRotate(grandfather); p->color = BLACK; grandfather->color = RED; }
3、
若新增结点挂在父结点的右子树
(前提),出现
“叔叔不存在”
或者
“叔叔存在且为黑”
,两种情况统一操作:
先进行两次“旋转”,先“左旋”后“右旋”,再进行“颜色调整”
,把新增(当前)结点颜色设置为
BLACK
,把祖父结点的颜色设置为
RED
分析规律:其实两次“旋转”,为了让第一次旋转操作可以恢复到2,就是祖父结点、父亲结点以及新增(当前)结点都在一条直线上。所以在这种情况下,可以先“左旋”,使之恢复到2,然后再进行和2一样的“右旋”操作。

部分核心代码:
//若新增结点挂在父结点的右子树(前提),出现"叔叔不存在"或者“叔叔存在且为黑”,两种情况统一操作:先进行两次“旋转”,先“左旋”后“右旋”,再进行“颜色调整” leftRotate(p); rightRotate(grandfather); cur->color = BLACK; grandfather->color = RED;
左三全部情况汇总如下:

(二)右三(结点插在祖父节点的右子树)
1、
“叔叔存在且为红”
的时候,只需要进行
颜色调整+继续向上调整
,即
把父亲结点和叔叔结点的颜色设置为
BLACK
,
把祖父结点的颜色设置为
RED
(若祖父结点为根结点,则再变黑);
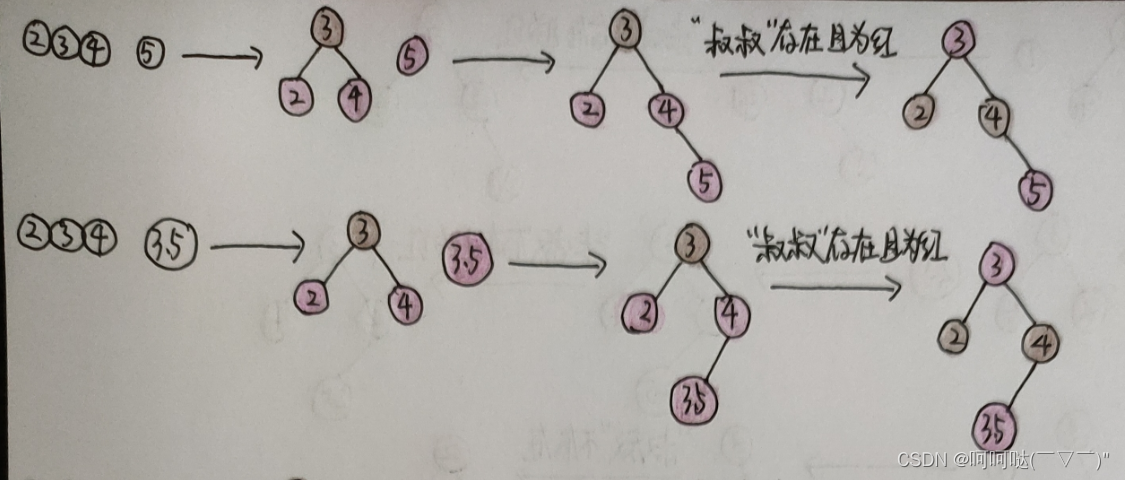
讨论可能出现的问题,新增结点加入之后,经过变色调整后,还需要继续向上调整

部分核心代码:
//1、uncle存在且为红 if (uncle && uncle->color == RED) { /* 变色 + 继续向上处理 */ //①变色 p->color = uncle->color = BLACK; grandfather->color = RED; //②继续向上处理 cur = grandfather; p = cur->parent; }
2、
若新增结点挂在父结点的右子树
(前提),出现”叔叔不存在”
或者
“叔叔存在且为黑”
,两种情况统一操作:
先进行一次“左旋”,再进行“颜色调整”
,
把父结点颜色设置为
BLACK
,
把祖父结点的颜色设置为
RED
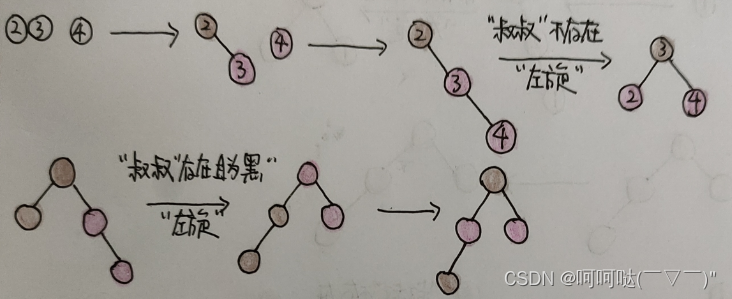
部分核心代码:
//2、若新增结点挂在父结点的右子树(前提),出现"叔叔不存在"或者“叔叔存在且为黑”,两种情况统一操作:先进行一次“左旋”,再进行“颜色调整” if (cur == p->right) { //单旋 leftRotate(grandfather); p->color = BLACK; grandfather->color = RED; }
3、
若新增结点挂在父结点的左子树
(前提),出现
“叔叔不存在”
或者
“叔叔存在且为黑”
,两种情况统一操作:
先进行两次“旋转”,先“右旋”后“左旋”,再进行“颜色调整”
,把新增(当前)结点颜色设置为
BLACK
,把祖父结点的颜色设置为
RED
分析规律:其实两次“旋转”,为了让第一次旋转操作可以恢复到2,就是祖父结点、父亲结点以及新增(当前)结点都在一条直线上。所以在这种情况下,可以先“右旋”,使之恢复到2,然后再进行和2一样的“左旋”操作。

部分核心代码:
//若新增结点挂在父结点的左子树(前提),出现"叔叔不存在"或者“叔叔存在且为黑”,两种情况统一操作:先进行两次“旋转”,先“右旋”后“左旋”,再进行“颜色调整” rightRotate(p); leftRotate(grandfather); cur->color = BLACK; grandfather->color = RED;
右三全部情况汇总如下:
左旋操作:
》》围绕p左旋:
①p是左孩子
pf pf
/ /
p pr(r)
/ \ / \
pl pr(r) ==> p rr(r)
/ \ / \
rl rr pl rl
②p是右孩子
pf pf
\ \
p pr(r)
/ \ / \
pl pr(r) ==> p rr(r)
/ \ / \
rl rr pl rl
void leftRotate(Node* p) { if (p) { Node* r = p->right; Node* rl = r->left; p->right = rl; if (rl) { rl->parent = p; } Node* parentParent = p->parent; //(双向) r->left = p;//p是r的左孩子 p->parent = r;//r是p的父亲 if (p == root) {//若p是根结点 root = r; r->parent = nullptr; } else { if (parentParent->left == p) { //p是左孩子 parentParent->left = r; } else { //p是右孩子 parentParent->right = r; } r->parent = parentParent; } } }
右
旋操作:
右旋
》》围绕p右旋:
①p是左孩子
pf pf
/ /
p pl(l)
/ \ ==》 / \
pl(l) pr ll p
/ \ / \
ll lr lr pr
②p是右孩子
pf pf
\ \
p pl(l)
/ \ ==> / \
pl(l) pr ll p
/ \ / \
ll lr lr pr
void rightRotate(Node* p) { if (p) { Node* l = p->left; Node* lr = l->right; p->left = lr; if (lr) { lr->parent = p; } Node* parentParent = p->parent; l->right = p; p->parent = l; if (p == root) { root = l; root->parent = nullptr; } else { if (parentParent->left == p) { parentParent->left = l; } else { parentParent->right = l; } l->parent = parentParent; } } }
比较结点值的大小
int compareTo(const pair<k, v> kv, Node* cur) { if (kv.first < cur->kv.first) return -1; else if (kv.first > cur->kv.first) return 1; else return 0; }
调整红黑树
void fixAfterPut(Node* p, Node* cur) { while (p && p->color == RED) { Node* grandfather = p->parent; if (p == grandfather->left) { Node* uncle = grandfather->right; //1、uncle存在且为红 if (uncle && uncle->color == RED) { /* 变色 + 继续向上处理 */ //①变色 p->color = uncle->color = BLACK; grandfather->color = RED; //②继续向上处理 cur = grandfather; p = cur->parent; } else {//2、uncle不存在/存在且为黑 if (cur == p->left) { //单旋 rightRotate(grandfather); p->color = BLACK; grandfather->color = RED; } else { //双旋 leftRotate(p); rightRotate(grandfather); cur->color = BLACK; grandfather->color = RED; } break; } } else { Node* uncle = grandfather->left; //1、uncle存在且为红 if (uncle && uncle->color == RED) { /* 变色 + 继续向上处理 */ //①变色 p->color = uncle->color = BLACK; grandfather->color = RED; //②继续向上处理 cur = grandfather; p = cur->parent; } else {//2、uncle不存在/存在且为黑 if (cur == p->right) { //单旋 leftRotate(grandfather); p->color = BLACK; grandfather->color = RED; } else { //双旋 rightRotate(p); leftRotate(grandfather); cur->color = BLACK; grandfather->color = RED; } break; } } } }
获取红黑树的高度
int Height() { return _Height(root); } int _Height(Node* root) { if (root == nullptr) { return 0; } int leftHeight = _Height(root->left); int rightHeight = _Height(root->right); return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1; }
完整代码:
/* 1、2-3-4树:新增元素+2节点合并(节点中只有1个元素)=3节点(节点中有2个元素) 红黑树:新增一个红色节点+黑色父亲节点=上黑下红(2节点)--------------不要调整 2、2-3-4树:新增元素+3节点合并(节点中有2个元素)=4节点(节点中有3个元素) 这里有6种情况(左3,右3,还有2个左中右不需要调整)----------------左3,右3需要调整,其余2个不需要调整 红黑树:新增红色节点+上黑下红=排序后中间节点是黑色,两边节点都是红色(3节点) 3、2-3-4树:新增一个元素+4节点合并=原来的4节点分裂,中间元素升级为父节点,新增元素与剩下的其中一个合并 红黑树:新增红色节点+爷爷节点黑,父节点和叔叔节点都是红色=爷爷节点变红,父亲和叔叔变黑,如果爷爷是根节点,则再变黑 */ #include<iostream> using namespace std; #include<vector> #include<cmath> #include<string> #include<vector> #define N 100 //#include "StringBuilder.h" enum Colour { RED, BLACK }; template<class k,class v> struct RBTreeNode { RBTreeNode<k, v>* left; RBTreeNode<k, v>* right; RBTreeNode<k, v>* parent; pair<k, v> kv; Colour color; RBTreeNode(const pair<k, v>& kv) :left(nullptr) , right(nullptr) , parent(nullptr) , kv(kv) , color(RED) {} }; template<class k, class v> class RBTree { typedef RBTreeNode<k, v> Node; public: RBTree() :root(nullptr) {} //插入结点 bool Insert(const pair<k, v>& kv) { if (root == nullptr) { root = new Node(kv); root->color = BLACK; return true; } Node* parent = nullptr; Node* cur = root; int res; while (cur) { res = this->compareTo(kv, cur); if (res == 1) { parent = cur; cur = cur->right; } else if (res == -1) { parent = cur; cur = cur->left; } else { return false; } } cur = new Node(kv); cur->color = RED;//新增节点 res = this->compareTo(kv, parent); //如果比较最终落在右子树,则直接将父节点右指针指向cur if (res == 1) { parent->right = cur; cur->parent = parent; } //如果比较最终落在左子树,则直接将父节点左指针指向cur else { parent->left = cur; cur->parent = parent; } //调整 fixAfterPut(parent,cur); root->color = BLACK; return true; } void fixAfterPut(Node* p,Node* cur) { while (p && p->color == RED) { Node* grandfather = p->parent; if (p == grandfather->left) { Node* uncle = grandfather->right; //1、uncle存在且为红 if (uncle && uncle->color == RED) { /* 变色 + 继续向上处理 */ //①变色 p->color = uncle->color = BLACK; grandfather->color = RED; //②继续向上处理 cur = grandfather; p = cur->parent; } else {//2、uncle不存在/存在且为黑 if (cur == p->left) { //单旋 rightRotate(grandfather); p->color = BLACK; grandfather->color = RED; } else { //双旋 leftRotate(p); rightRotate(grandfather); cur->color = BLACK; grandfather->color = RED; } break; } } else { Node* uncle = grandfather->left; //1、uncle存在且为红 if (uncle && uncle->color == RED) { /* 变色 + 继续向上处理 */ //①变色 p->color = uncle->color = BLACK; grandfather->color = RED; //②继续向上处理 cur = grandfather; p = cur->parent; } else {//2、uncle不存在/存在且为黑 if (cur == p->right) { //单旋 leftRotate(grandfather); p->color = BLACK; grandfather->color = RED; } else { //双旋 rightRotate(p); leftRotate(grandfather); cur->color = BLACK; grandfather->color = RED; } break; } } } } int compareTo(const pair<k, v> kv, Node* cur) { if (kv.first < cur->kv.first) return -1; else if (kv.first > cur->kv.first) return 1; else return 0; } //左旋 /* 》》围绕p左旋: ①p是左孩子 pf pf / / p pr(r) / \ / \ pl pr(r) ==> p rr(r) / \ / \ rl rr pl rl ②p是右孩子 pf pf \ \ p pr(r) / \ / \ pl pr(r) ==> p rr(r) / \ / \ rl rr pl rl */ void leftRotate(Node* p) { if (p) { Node* r = p->right; Node* rl = r->left; p->right = rl; if (rl) { rl->parent = p; } Node* parentParent = p->parent; //(双向) r->left = p;//p是r的左孩子 p->parent = r;//r是p的父亲 if (p == root) {//若p是根结点 root = r; r->parent = nullptr; } else { if (parentParent->left == p) { //p是左孩子 parentParent->left = r; } else { //p是右孩子 parentParent->right = r; } r->parent = parentParent; } } } //右旋 /* 》》围绕p右旋: ①p是左孩子 pf pf / / p pl(l) / \ ==》 / \ pl(l) pr ll p / \ / \ ll lr lr pr ②p是右孩子 pf pf \ \ p pl(l) / \ ==> / \ pl(l) pr ll p / \ / \ ll lr lr pr */ void rightRotate(Node* p) { if (p) { Node* l = p->left; Node* lr = l->right; p->left = lr; if (lr) { lr->parent = p; } Node* parentParent = p->parent; l->right = p; p->parent = l; if (p == root) { root = l; root->parent = nullptr; } else { if (parentParent->left == p) { parentParent->left = l; } else { parentParent->right = l; } l->parent = parentParent; } } } void InOrder() { _InOrder(root); } //中序遍历 void _InOrder(Node* root) { if (root == nullptr) { return; } _InOrder(root->left); cout << root->kv.first << ":" << root->kv.second << endl; _InOrder(root->right); } /* 检测是否满足红黑树的性质:任意选取一条路径找出黑色结点的个数作为基准值,然后依次与其他 路径比较,如果都相同则满足红黑树的性质。 */ bool IsBalance() { if (root && root->color == RED) { cout << "根结点不是黑色" << endl;//为了测试 return false; } //最左路径黑色结点数量做基准值 int banchmark = 0;//保存最左侧路径中黑色结点的个数 Node* left = root; while (left) { if (left->color == BLACK) ++banchmark; left = left->left; } int blackNum = 0;//递归遍历时记录黑色结点的个数 return _IsBalance(root, banchmark, blackNum); } bool _IsBalance(Node* root, int banchmark, int blackNum) { //走到null之后,判断banchmark和blackNum是否相等 if (root == nullptr) { if (banchmark != blackNum) { cout << "存在路径黑色结点的数量不相等" << endl;//为了测试 return false; } return true; } if (root->color == RED && root->parent->color == RED) { cout << "出现了连续的红色结点" << endl;//为了测试 return false; } if (root->color == BLACK)// 统计黑色节点的个数 { ++blackNum; } return _IsBalance(root->left, banchmark, blackNum) && _IsBalance(root->right, banchmark, blackNum); } int Height() { return _Height(root); } int _Height(Node* root) { if (root == nullptr) { return 0; } int leftHeight = _Height(root->left); int rightHeight = _Height(root->right); return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1; } Node* getRoot() { return this->root; } private: Node* root; }; template<class k, class v> class TreeOperation { typedef RBTreeNode<k, v> Node; /* 树的结构示例: 1 / \ 2 3 / \ / \ 4 5 6 7 */ // 用于获得树的层数 public: int getTreeDepth(Node* root) { if (root == nullptr) return 0; else { int ldep = getTreeDepth(root->left); int rdep = getTreeDepth(root->right); return (ldep < rdep) ? rdep + 1 : ldep + 1; } } void writeArray(Node* currNode, int rowIndex, int columnIndex, string** res, int treeDepth) { // 保证输入的树不为空 if (currNode == nullptr) return; // 0、默认无色 //res[rowIndex][columnIndex] = String.valueOf(currNode.getValue()); //1、颜色表示 if (currNode->color == BLACK) {//黑色,加色后错位比较明显 res[rowIndex][columnIndex] = ("\033[40;3m" + currNode->kv.second + "\033[0m"); //cout << "-----------------------------------------" << res[rowIndex][columnIndex] << endl; } else { res[rowIndex][columnIndex] = ("\033[31;3m" + currNode->kv.second + "\033[0m"); //cout << "=========================================" << res[rowIndex][columnIndex] << endl; } //2、R,B表示 //res[rowIndex][columnIndex] = String.valueOf(currNode.getValue()+"-"+(currNode.isColor()?"B":"R")+""); // 计算当前位于树的第几层 int currLevel = ((rowIndex + 1) / 2); // 若到了最后一层,则返回 if (currLevel == treeDepth) return; // 计算当前行到下一行,每个元素之间的间隔(下一行的列索引与当前元素的列索引之间的间隔) int gap = treeDepth - currLevel - 1; // 对左儿子进行判断,若有左儿子,则记录相应的"/"与左儿子的值 if (currNode->left != nullptr) { res[rowIndex + 1][columnIndex - gap] = "/"; writeArray(currNode->left, rowIndex + 2, columnIndex - gap * 2, res, treeDepth); } // 对右儿子进行判断,若有右儿子,则记录相应的"\"与右儿子的值 if (currNode->right != nullptr) { res[rowIndex + 1][columnIndex + gap] = "\\"; writeArray(currNode->right, rowIndex + 2, columnIndex + gap * 2, res, treeDepth); } } void show(Node* root) { if (root == nullptr) printf("EMPTY!"); //printf("=============="); // 得到树的深度 int treeDepth = getTreeDepth(root); // 最后一行的宽度为2的(n - 1)次方乘3,再加1 // 作为整个二维数组的宽度 int arrayHeight = treeDepth * 2 - 1; int arrayWidth = (2 << (treeDepth - 2)) * 3 + 1; /*printf("==============%d \n", arrayHeight); printf("==============%d \n", arrayWidth);*/ // 用一个字符串数组来存储每个位置应显示的元素 //string res[arrayHeight][arrayWidth]; int rows = arrayHeight; int cols = arrayWidth; //动态创建二维字符数组arr[m][n] string** res; res = new string * [arrayHeight]; //创建行指针 for (int i = 0; i < arrayHeight; i++) res[i] = new string[arrayWidth]; //为每行分配空间 // 对数组进行初始化,默认为一个空格 for (int i = 0; i < arrayHeight; i++) { for (int j = 0; j < arrayWidth; j++) { res[i][j] = " "; } } // 从根节点开始,递归处理整个树 writeArray(root, 0, arrayWidth / 2, res, treeDepth); for (int i = 0; i < arrayHeight; i++) { vector<string> strVector = {}; for (int j = 0; j < arrayWidth; j++) { cout<< res[i][j]; int tempStrLen = res[i][j].length(); if (tempStrLen > 1 && j <= arrayHeight - 1) { j += tempStrLen > 4 ? 2 : tempStrLen - 1; } //strVector.push_back(res[i][j]); /*if (res[i][j].length() > 1 && j <= arrayHeight - 1) { j += res[i][j].length() > 4 ? 2 : res[i][j].length() - 1; }*/ } cout << endl; /*string str=""; for (vector<string>::const_iterator it = strVector.begin(); it != strVector.end(); it++) { str.append(*it); } cout << str << endl;*/ } } }; void insertOpt() { RBTree<string, string> t; int inputV = 0; string str = ""; while (true) { printf("请输入你要插入的节点:"); scanf_s("%d", &inputV); str = to_string(inputV); //这里代码最多支持3位数,3位以上的话红黑树显示太错位了,这里就不重构代码了,大家可自行重构 if (str.length() == 1) { str = "00" + str; } else if (str.length() == 2) { str = "0" + str; } t.Insert(make_pair(str, str)); TreeOperation<string, string> Tp; Tp.show(t.getRoot()); } } void TestRBTree() { //RBTree<int, int> t; RBTree<string, string> t; //string a[] = { "5","4","3","2","1","0"}; //string a[] = { "16","3","7","11","9","26","18","14","15"}; //string a[] = { "4","2","6","1","3","5","15","7","16","14"}; //string a[] = { "4","2","6","1","3","5","15","7","16","14","8","9","10","11","12","13","14"}; string a[] = { "6","4","10","8","3","7","9"}; for (auto str : a) { if (str.length() == 1) { str = "00" + str; } else if (str.length() == 2) { str = "0" + str; } t.Insert(make_pair(str, str)); //cout << "Insert" << e << ":" << t.IsBalance() << endl; } /*t.InOrder(); cout << t.IsBalance() << endl; cout << t.Height() << endl;*/ //TreeOperation<int, int> Tp; TreeOperation<string, string> Tp; Tp.show(t.getRoot()); } int main() { /*TestRBTree(); cout << endl; cout << endl; cout << endl;*/ insertOpt(); system("pause"); return 0; }
效果展示如下: