四足机器人学习笔记（足端轨迹规划）

不管是基于位置控制还是力矩控制亦或是其他一些控制方式，均需要进行足端的轨迹规划，来使四足机器人能够成功跨越障碍物。因此对于四足机器人足端轨迹方法进行了汇总。

1. 摆线轨迹

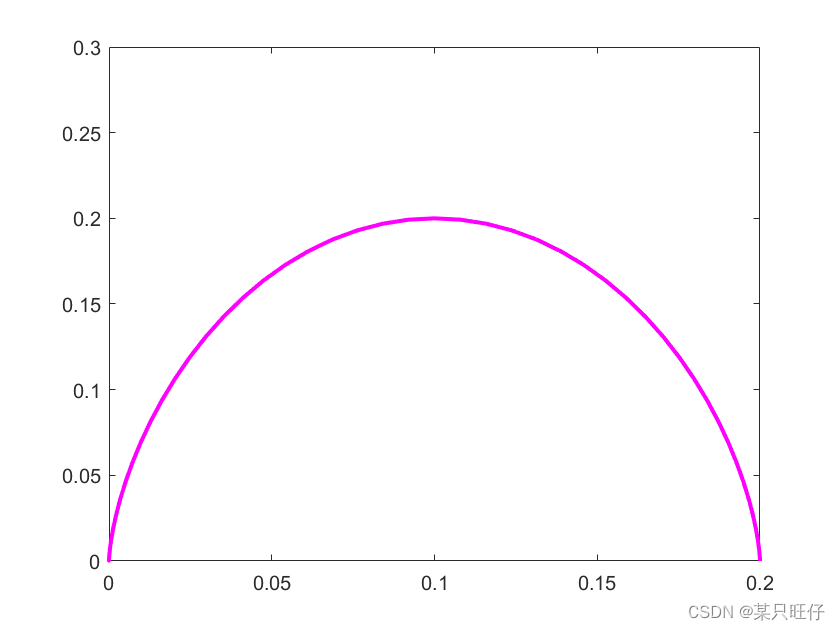
若使用位置控制模式，可以将足端轨迹规划为此种

将1，3腿作为一组，2，4腿作为另一组分时进行摆动。

当一组腿进行摆动时：

$\sigma = 2*pi*t/(\varphi *Ts)$

当轮到另一组腿进行摆动时，

$\sigma = 2*pi *(t-Ts*\varphi )/(\varphi*Ts )$

并代入下面的公式中计算，即可得到此时摆动相和支撑相（我认为也不是严格的支撑相毕竟像相对于地面仍然有位移）的足端规划轨迹

$zep = h*(1-cos(\sigma ))/2$

$xep_b = (xf-xs)*((\sigma -sin(\sigma ))/(2*pi))+xs$
$xep_z = (xs-xf)*((\sigma -sin(\sigma ))/(2*pi))+xf$

参数解释

t ——-在整个步态周期循环时间里从开始到某一时刻的时间

Ts ——步态循环周期

faai —- 占空比

zep —- 在地面坐标系下(z轴竖直向上)的规划后得到的坐标

h —- 抬腿高度

xep_b —- 某一组腿（此时设定为摆动腿）在地面坐标系下x轴（狗前进方向定为x轴正方向）的坐标

xs —- 足端x轴起始坐标

xf —- 足端x轴目标坐标

2. 类正弦轨迹

$gp = 0:0.01:1$

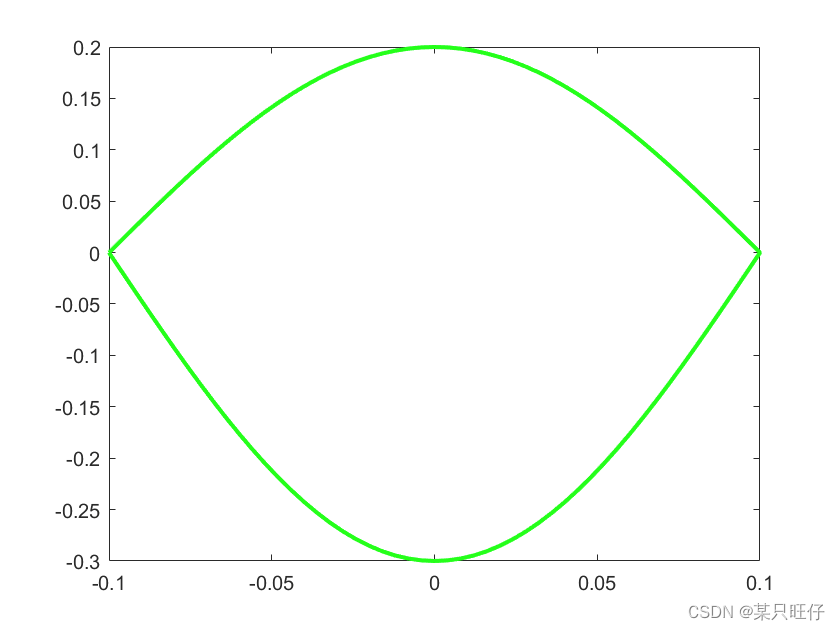
如果gp<flightPercent:

$x = (gp/ flightPercent)*stepLength - stepLength/2$

$y = -upAMP*sin(pi*gp/flightPercent)+stanceHeight$

如果gp>=flightPercent

$percentBack = (gp-flightPercent)/(1-flightPercent)$

$x = -percentBack*stepLength+stepLength/2$

$y = downAMP*sin(pi*percentBack)+stanceHeight$

对应的matlab代码：

3. 三次多项式

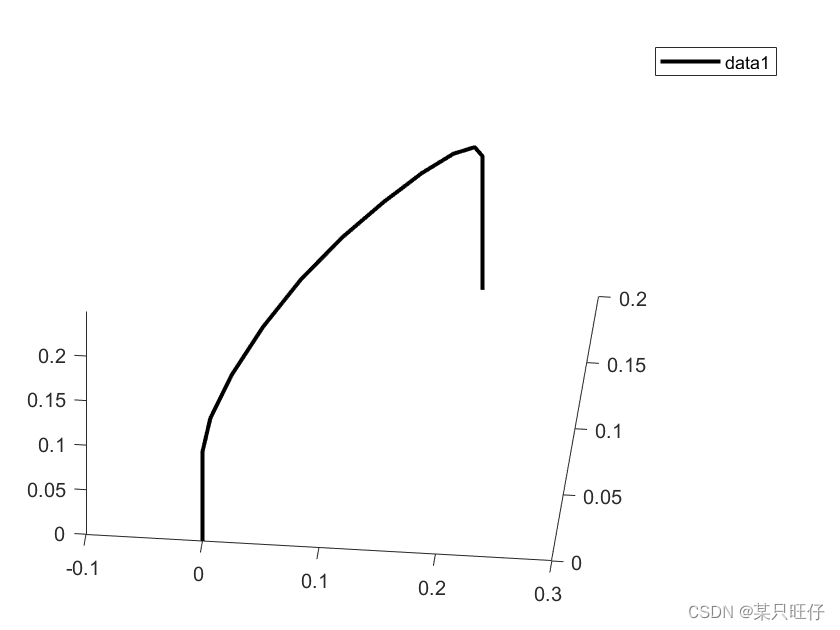
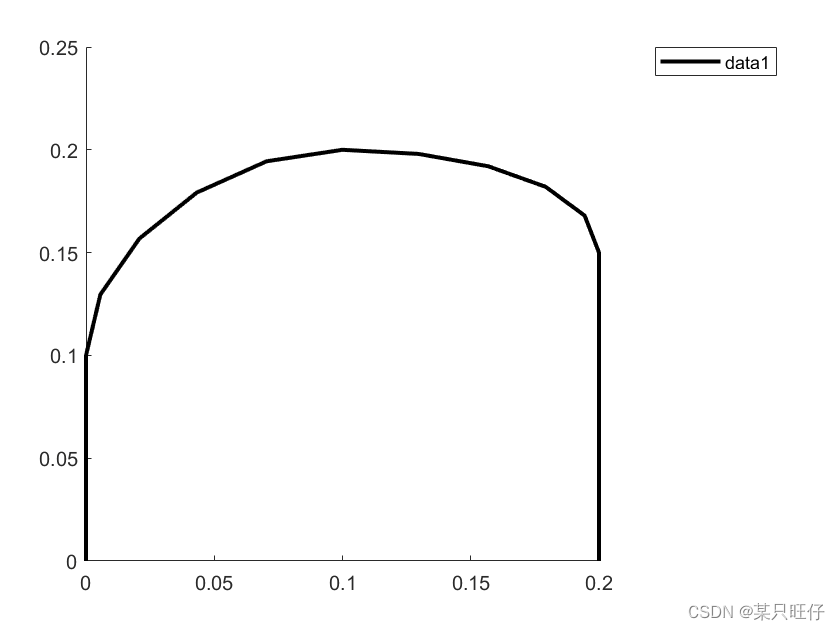
图1为整个三维空间的足端规划轨迹图2为X-Z和Y-Z平面上的轨迹投影

整个轨迹规划分为3段式：（其中x轴和y轴上规划方式相同，z轴上时间划分与其不同）

x,y轴：

（1）当t<Tf/4时

$x = -4*Vx *t^2/Tf + Vx*t+x_0$

$y = -4*Vy*t^2/Tf+Vy*t+y_0$

（2）当t>=Tf/4 并且 t<3*Tf/4时

$x = (-4*Tf*Vx-16*xT+16*x_0)*t^3/Tf^3 + (7*Tf*Vx+24*xT-24*x_0)*t^2/Tf^2+(-15*Tf*Vx-36*xT+36*x_0)*t/(4*Tf)+(9*Tf*Vx+16*xT)/16$

$y = (-4*Tf*Vy-16*xT+16*y_0)*t^3/Tf^3 + (7*Tf*Vy+24*yT-24*y_0)*t^2/Tf^2+(-15*Tf*Vy-36*yT+36*y_0)*t/(4*Tf)+(9*Tf*Vy+16*yT)/16$

（3）当t>=3*Tf/4 并且 t<=Tf时

$x = xT$

$y = yT$

z轴

（1）当t <Tf/2时

$z = 16*(z_0-z_h)*t^3/Tf^3+12*(z_h-z0)*t^2/Tf^2+z_0$

（2）当t>=Tf/2 并且 t<3*Tf/4时

$z = 4*(z_0-z_h)*t^2/Tf^2-4*(z_0-z_h)*t/Tf+z_0$

（3）当t>=3*Tf/4 并且 t<=Tf时

$z = 4*(z_0-z_h)*t^2/Tf^2-4*(z_0-z_h)*t/Tf+z0$

参数解释
Tf	一个周期内摆动相时间
x,y,z	在地面坐标系下x,y,z轴规划的足端实时坐标
Vx,Vy,Vz	在地面坐标系下x沿着三个轴的实时速度
t	在该摆动相开始时到某一时刻的时间间隔
xT，yT，zh	三个轴上一个周期内期望的落地点坐标
x0，y0，z0	三个轴上一个周期内足端初始位置的坐标

对应的matlab代码：（其中将速度值设为恒定实际使用中需要测得获得速度值）

4. 改进型等速运动

在原本的等速运动基础到，考虑到由于等速运动带来的位移函数在抬腿时和落地时数值发生突变，因此使用正弦运动规律与等速运动规律相结合。

（1）
$0\leq t\leq\frac{T}{4}$

$S = \frac{AT}{4\pi }*(t-\frac{T}{4\pi }sin(\frac{4\pi t}{T}))$

（2）
$\frac{T}{4}\leq t\leq \frac{3}{4}T$

$S = \frac{AT^2}{16\pi }+\frac{2AT}{4\pi }(t-\frac{T}{4})$

（3）
$\frac{3}{4}T\leq t\leq T$

$S = \frac{5AT^2}{16\pi }+\frac{AT}{4\pi }(t-\frac{3}{4}T)+\frac{AT^2}{16\pi ^2}sin(\frac{4\pi(t-\frac{3}{4}T) }{T})$

根据约束：t = 0 时 S = 0 ; t = T时，S = S0;

得出系数A的值

$A = \frac{8\pi S_{0}}{3T^2}$

其中T表示的是摆动周期，S0 表示的是运动行程

位移曲线图：

速度曲线图和加速度曲线图：

matlab代码：（只写了位移函数板块）

clear;clc
T = 1;
S0 = 250;
A = 8*pi*S0/3/T^2;
syms t;

t = 0:0.01:T/4;
S = A.*T./4./pi.*(t-T./4./pi.*sin(4.*pi.*t./T));

t1 = T/4:0.01:3*T/4;
S1 = A.*T^2/16/pi + 2.*A.*T./4./pi.*(t1-T./4);

t2 = 3*T/4:0.01:T;
S2 = 5.*A*T^2/16/pi+A.*T/4/pi*(t2-3*T/4)+A*T^2/16/pi/pi*sin(4*pi*(t2-3*T/4)/T);

t_all = [t t1 t2];
S_all = [S S1 S2];
plot(t_all,S_all);

原文链接：https://blog.csdn.net/qq_54543084/article/details/125281942

你可能也喜欢