D-Separation
很多的机器学习模型都可以用概率的角度去解释(可以看MLAPP和PRML这两本书),其中一类重要的模型就是概率图模型,而是概率图模型的灵魂就是模型变量间的条件独立性。
因为有了独立性,才有了各种不同的概率图模型,比如LDA,HMM等等模型。那么概率图中,变量间的独立性是怎么体现的呢?D-分离准则就是一种简单的技巧去判断一个概率图中的独立性的。
简单的说,如果在概率图模型中,比如说X,Y两个节点没有边,使得X和Y之间肯定存在某种独立性,这种独立性可以是在某个子集Z的条件下使得他们独立,也可能是他们两个本身就是独立的,这时我们称X,Y之间是D-分离的。现在先给出D-分离的准则:
定义:
当路径p被结点集Z,d-分离(或被blocked掉)时,当且仅当以下条件成立:
- 若p包含形式如下的链i->m->j 或i<-m->j,则结点m在集合Z中。
- 若p中包含collider(碰撞点)i->m<-j,则结点m不在Z中且m的子代也不在Z中。
更进一步说,如果Z将X和Y d-separate,当且仅当Z将X,Y之间的每一条路径都block掉。
接下来逐步的介绍上述的准则,我们可以拆分成3个规则来考虑:
首先,这里我们先说明一下path,我们说两个结点之间的path的时候是不管他们之间边的方向的。
没有条件集的独立性
规则1
:
如果x到y的任一path(路径)都经过collider(碰撞点),则x和y独立。注意,这里的路径是忽略边的方向的,而碰撞点是指有多个箭头指向的它的节点,即类似于下图的s->t<-u。
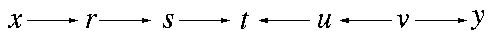
现在我们看看这个图变量之间的独立性是怎样的。先考虑x和t的路径:x-r-s-t。这条路径中并不存在碰撞点,所以x和t不独立,同样地,t和y、u、v都不独立。然而,对于变量x到y而言,x,y之间的路径必然会经过碰撞点t,所以x和y是独立,同样地,在碰撞点两侧的变量都是独立的,比如x和v,s和u,r和u也是独立的。
一般的条件独立
那么如果一条路径中没有碰撞点,怎么才能让他们独立呢?我们还能使用条件独立的性质,只要条件集Z能够将一条路径block掉,那么就可以让两个变量独立。注意的是,当碰撞点或碰撞点的子代出现在条件集的时候要小心,很有可能会导致不同的结果,这个问题我们留到规则3。现在我们先假设条件集中不存在碰撞点。
规则2
:
当x到y的之间的任一路径都经过Z中的节点,且Z并不包含碰撞点或碰撞点的子代,则x和y独立。
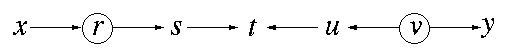
如图,设结点集Z={r, v}(图中画圈的节点),根据规则2,x和s是条件独立的,因为x和s之间的路径被block掉了,同样地,u和y也是条件独立的。
当collider作为条件集
现在我们先看看collider成为条件集的时候会发生什么。我们考虑一个例子

这里显然IQ和难度是独立的,他们共同决定成绩的高低,于是成绩是一个collider,而不同成绩会导致不同排名,所以排名是成绩的子代。现在如果我们已经知道一个人的成绩是多少,那么神奇的事情发生了,如果我们知道一个人IQ很低,但成绩很高,那么我们可以推断出难度肯定很低;同理我们知道成绩很高,但难度很大,那么可以推断出IQ很高。原本IQ和难度两个独立的变量在成绩的条件下变得不独立的。
同理,因为ABCD等级是由不同成绩划分出来的,也包含了成绩的信息,所以我们知道一个人的等级同样可以推断出一个人的IQ和难度。因此当条件集是collider的时候,会反而使得两个独立的变量变得不独立。这就是我们判断条件独立性的时候要小心的地方。接下来是规则3,
规则3
:
当碰撞点或碰撞点的子孙节点为集合Z的成员时,该碰撞点不再截断路径。
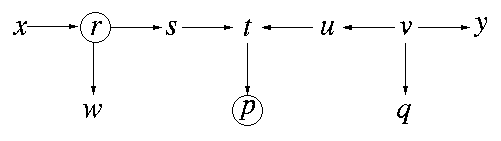
设结点集Z={r, p}(图中画圈的节点),根据规则3,在给定Z的情况下,s和y不独立,因为t的孩子节点p在集合Z中,所以t没有办法像规则1一样截断路径s-t-u-v-y,与此相反,条件集p使得s和u变得不独立了。然而在这里,x和u是独立的,虽然t不能截断它,但是r可以截断它(根据规则2)。
参考资料
Pearl, Judea. Causality. Cambridge university press, 2009. Page 16.