博客

**

kmeans聚类详解

**


(1) kmeans简介


K-means算法是很典型的

基于距离

的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

k个初始类聚类中心点的选取对聚类结果具有较大的影响，因为在该算法第一步中是随机的选取任意k个对象作为初始聚类的中心，初始地代表一个簇。该算法在每次迭代中对数据集中剩余的每个对象，根据其与各个簇中心的距离将每个对象重新赋给最近的簇。当考察完所有数据对象后，一次迭代运算完成，新的聚类中心被计算出来。如果在一次迭代前后，J的值没有发生变化，说明算法已经收敛。


(2)算法过程如下


1.计算欧氏距离

2.随机选取k个初始聚类中心点

3.更新簇的中心点

4.迭代,直到收敛

通常停止迭代的条件:

• 达到指定的迭代次数
• 质心不再发生明显的变化,即收敛
  
  这里采用了设置迭代次数而停止迭代
  
  
  (3)实现步骤
  
  
  导入库和模块
  
  

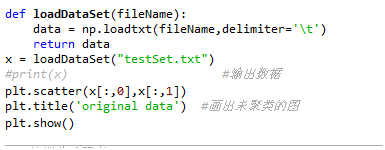
导入数据.画出未聚类的图





计算欧氏距离



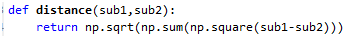
初始化质心, 将给定数据集构建一个包含K个随机质心的数组



开始kmeans聚类



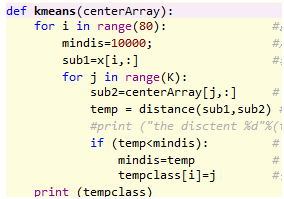
更新质心



开始迭代,迭代10次



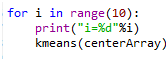
第一次迭代



第二次迭代



第三次迭代



第四次迭代



第五次迭代



第六次迭代



第七次迭代



第八次迭代



第九次迭代



第十次迭代



最后画出聚类结果图



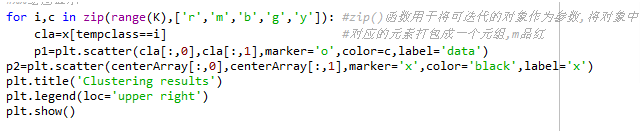
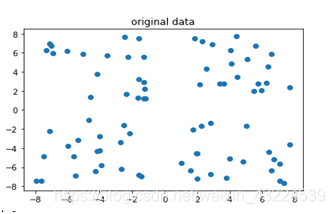
最后的聚类结果图,聚成了4类,在k=4的时候聚类效果最好





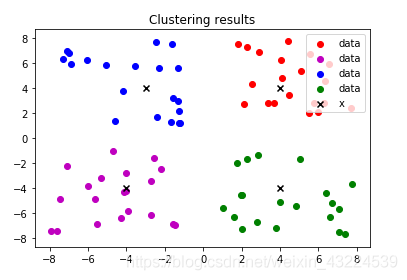
(4)对kmeans算法的认识



• 聚类是一种无监督的学习方法

• K均值算法需要用户指定创建的簇数k

• K均值算法在大数据集上收敛较慢


优点


K-Means聚类算法的优点主要集中在:

1.算法快速、简单;

2.对大数据集有较高的效率并且是可伸缩性的;

3.时间复杂度近于线性，而且适合挖掘大规模数据集。K-Means聚类算法的时间复杂度是O(nkt) ,其中n代表数据集中对象的数量，t代表着算法迭代的次数，k代表着簇的数目


缺点


① 在 K-means 算法中 K 是事先给定的，这个 K 值的选定是非常难以估计的

② 在 K-means 算法中，首先需要根据初始聚类中心来确定一个初始划分，然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响，一旦初始值选择的不好，可能无法得到有效的聚类结果，这也成为 K-means算法的一个主要问题。

③ 从 K-means 算法框架可以看出，该算法需要不断地进行样本分类调整，不断地计算调整后的新的聚类中心，因此当数据量非常大时，算法的时间开销是非常大的。所以需要对算法的时间复杂度进行分析、改进，提高算法应用范围。

(5)源代码展示

"""
Created on Mon Dec 10 13:53:35 2018

@author: liushengzhen
"""
#%%导入使用的库
import numpy as np
import random
import matplotlib.pyplot as plt  
                                                  
#%%导入数据                                         
def loadDataSet(fileName):
    data = np.loadtxt(fileName,delimiter='\t')
    return data
x = loadDataSet("testSet.txt")
#print(x)                      #输出数据
plt.scatter(x[:,0],x[:,1])   
plt.title('original data')  #画出未聚类的图
plt.show()

#%%计算欧氏距离
def distance(sub1,sub2):                          #numpy的数组可以对一个向量做减法，得到的还是一个向量
    return np.sqrt(np.sum(np.square(sub1-sub2))) #对向量做平方,求和,开方,得到sub1和sub2的欧式距离
#%%初始化质心    
K=4 
# 将给定数据集构建一个包含K个随机质心的数组           
tempclass=np.zeros(x.shape[0]) #获得x的第0列的维度(行数)
center = random.sample(range(x.shape[0]),K)#从x的第0列数中随机挑选k个数
centerArray = x[center,:]      #从x中获得以center的序列内容为行的向量，列数是从第0列到最后一列
#至此完成了对 kmeans 中心点的生成(质心)

#%%kmeans聚类
def kmeans(centerArray):
    for i in range(80):               #因为是80行数据，这里要准备逐条遍历x的80行数据
        mindis=10000;                 #质心的最小距离  
        sub1=x[i,:]                   #获取矩阵x的第i行数据
        for j in range(K):            #遍历质心
            sub2=centerArray[j,:]     # 按行读取质心列表中的行向量
            temp = distance(sub1,sub2) # 逐个元素计算与质心的距离
            #print ("the disctent %d"%(temp)) #输出的是80个数据依次到4个质心的距离(一次迭代320)
            if (temp<mindis):         # 在k个质心里面选择距离最小的
                mindis=temp           #
                tempclass[i]=j        #得到样本i 距离最近质心
    print (tempclass)
#%%
    #更新质心
    for j in range(K): #遍历质心                    #按照质心个数，统计每个质心下面的样本
        tempclassResult = x[tempclass==j]  #从聚类结果里面分别拿到每个类的样本
        x1=np.mean(tempclassResult[:,0])   #取出tempclassResult里面第0列的值序列，并对这个序列计算均值
        x2=np.mean(tempclassResult[:,1])   
        centerArray[j,:]=[int(x1),int(x2)] #更新质心数组里面的质心坐标

#%%开始迭代        
#迭代10次
for i in range(10):
    print("i=%d"%i)
    kmeans(centerArray)
        
#%%绘图显示  
for i,c in zip(range(K),['r','m','b','g','y']): #zip()函数用于将可迭代的对象作为参数,将对象中
    cla=x[tempclass==i]                         #对应的元素打包成一个元组,m品红
    p1=plt.scatter(cla[:,0],cla[:,1],marker='o',color=c,label='data')  
p2=plt.scatter(centerArray[:,0],centerArray[:,1],marker='x',color='black',label='x')
plt.title('Clustering results')  
plt.legend(loc='upper right')  
plt.show()  

若有不足之处希望读者评论,一起进步!!!