快速算法

简介：

快速排序是基于分治技术的重要排序算法，排序算法按照元素的值对它们进行划分。

划分是对给定数组中的元素的重新排序，使得

[

]

A[s]

$A [s]$

左边的元素都小于等于

[

]

A[s]

$A [s]$

，而右边

[

]

A[s]

$A [s]$

右边的元素都大于等于

[

]

A[s]

$A [s]$

。

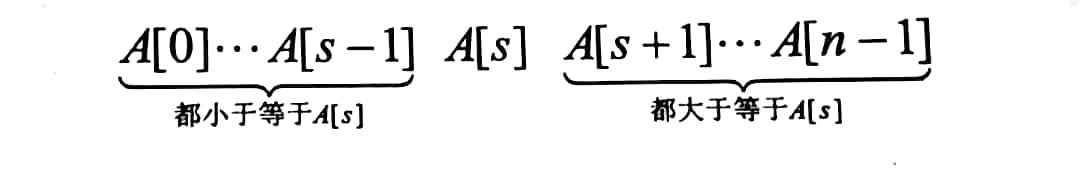
在这里插入图片描述

显然，建立了一个划分以后，

[

]

A[s]

$A [s]$

已经位于它在有序数组中的最终结果，接下来我们可以继续对

[

]

A[s]

$A [s]$

前和

[

]

A[s]

$A [s] $

后的子数组分别进行排序(例如，使用同样的方法)。

注意，它和合并排序不同之处在：

在合并排序算法中，将问题划分为两个子问题，是很快的，算法的主要工作在于合并子问题的解；
在快速排序中，算法的主要工作在于划分阶段，而不需要再去合并子问题的解了。

动态演示过程：

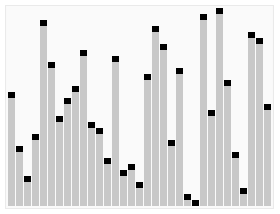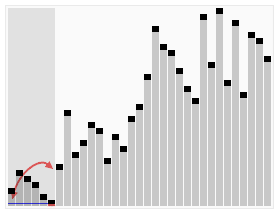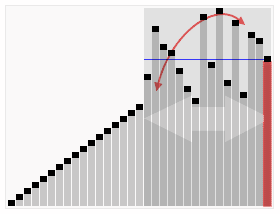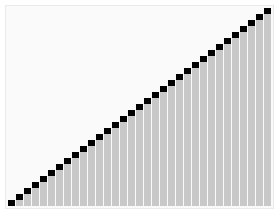
在这里插入图片描述

下面是快速排序的伪代码：

算法 Quicksort(A[l..r])
	  //用QuickSort对子数组排序
	  //输入：数组A[0..n-1]中的子数组A[l..r],由左右下标和r定义
	  //输出：非降序排列的子数组A[l..r]
	  if l < r:
			s <- Partition (A[l..r]) // s是分裂位置
			Quicksort(A[l..s-1])
			Quicksort(A[s+1..l])

下面这段伪代码实现了划分的过程：

算法 HoarePartition(A[l..r])
		//以第一个元素为中轴，对子数组进行划分
		//输入：数组A[0..n-1]中的子数组A[l..r],由左右下标l和r定义
		//输出：A[l..r]的一个划分，分裂点的位置作为函数的返回值
		p <- A[l]
		i <- l; j <- r+1
		repeat
			repeat i <- i+1 until A[i] >= p
			repeat j <- j-1 until A[j] <= p
			swap(A[i], A[j])
		until i >= j
		swap(A[i], A[j])	//当i>=j撤销最后一次交换
		swap(A[l], A[j])
		return j

排序过程：

在这里插入图片描述

C语言代码1：

int qsort(int *a,int left,int right){
    if (right <= left)
        return -1;
    int pivot = a[right];
    int i = left;
    int j = right - 1;

    //从前向后扫描，不需要判断是否会出现越界问题
    while(true){
        while(a[i++] < pivot);

        //从后向前扫描，要防止越界
        while(a[j] > pivot && j >= left){
            j--;
        }
        if (i < j)
            swap(a[i++],a[j--]);
        else{
            break;
        }
    }
    swap(a[i],pivot); // 最后一趟是将a[i]与pivot交换
    qsort(a,left,i -1);
    qsort(a,i+1,right);
    return 0;
}

C语言代码2：

//  划分算法
int Partition(RcdType rcd[], int low, int high){
    //  对子序列rcd[low..high]进行一次划分，并返回枢轴应当所处的位置
    //  使得在枢轴之前的关键字均不大于它的关键字，枢轴之后的关键字均不小于它的关键字
    rcd[0] = rcd[low];      //  将枢轴移至数组的闲置单元
    while (low < high){     //  low和high从待排序列的两端交替地向中间移动
        while (low < high && rcd[high].key >= rcd[0].key)   --high;
        rcd[low] = rcd[high];   //  将比枢轴关键字小得关键字移至低端
        while (low < high && rcd[low].key <= rcd[0].key)    ++low;
        rcd[high] = rcd[low];   //  将比枢轴关键字打的关键字移至高端
    }
    rcd[low] = rcd[0];  //  枢轴关键字移到正确位置
    return low;         //  返回枢轴的位置
}

//  快速排序
void QSort(RcdType rcd[], int s, int t){
    //  对记录序列rcd[s..t]进行快速排序
    int privotloc;
    if (s < t){         //  长度大于1
        privotloc = Partition(rcd, s, t);   //  对rcd[s..t]进行划分并返回枢轴位置
        QSort(rcd, s, privotloc - 1);       //  对枢轴之前的子序列递归快排
        QSort(rcd, privotloc + 1, t);       //  对枢轴之后的子序列递归快排
    }
}

//  对记录的顺序表L进行快速排序
void QuickSort(RcdSqList &L){
    QSort(L.rcd, 1, L.length);
}

快速排序优化：

更好的中轴选择方法

随机选取法：

原因

:在待排序列是部分有序时，固定选取枢轴使快排效率低下，要缓解这种情况，就引入随机选取枢轴

思路

:使用随机数生成函数生成一个随机数rand，随机数的范围在[left, right], 并用此随机数为下标对应的元素a[rand]作为中轴，并与最后一个元素a[right]交换，然后进行与选取最后一个元素作为中轴的快排一样的算法即可

例如随机快速排序(randomized quicksort)，它使用随机的元素作为中轴；

int random(int left,int right){
    return rand() % (right - left + 1) + left;
}

void Qsort(int *a,int left,int right){
    if (left >= right)
    {
        return;
    }
    //随机选取一个元素作为枢轴，并与最后一个元素进行交换
    int ic = random(left,right);
    swap(a[ic],a[right]);

    int midIndex = data[right];
    int i = left;
    int j = right - 1;

    while(true){
        //找大于枢轴的数据
        while(a[i++] < midIndex);

        //找到小于枢轴的数据
        while(a[j] > midIndex && j >= left){
            j--;
        }
        //数据已经找到，准备交换
        if (i < j)
        {
            swap(a[i++],a[j--]);
        }
        else{
            break;
        }
    }
    swap(a[i],midIndex); //将枢轴放在正确的位置
    Qsort(a,left,i -1);
    Qsort(a,i+1,right);
}

三数取中

原因

:虽然随机选取枢轴时，减少出现不好分割的几率，但是最坏情况还是

(

)

O(n^2)

$O (n^{2})$

，要缓解这种情况，就引入了三数取中选取枢轴。

思路

:假设数组被排序的范围

left

$l e f t$

和

right

$r i g h t$

，

(

)

center=(left+right)/2

$c e n t e r = (l e f t + r i g h t) / 2$

, 对于a[left]和a[right]和a[center]进行适当排序，取中值为中轴，将最小者放a[left]，最大者放a[right]，把中轴元与a[right-1]交换，并在分割阶段将i和j初始化为left+1和right-2。然后使用双向描述法，进行快排。

例如三平均划分法(median-of-three method)，它以数组最左边、最右边和最中间的元素的中位数作为中轴。

分割好处：

1.将三元素中最小者被分到a[left]、最大者分到a[right]是正确的，因为当快排一趟后，比中轴小的放到左边，而比中轴大的放到右边，这样就在分割的时候把它们分到了正确的位置，减少了一次比较和交换。

2.在前面所说的所有算法中，都有双向扫描时的越界问题，而使用这个分割策略则可以解决这个问题。因为i向右扫描时，必然会遇到不小于中轴的数a[right-1]，而j在向左扫描时，必然会遇到不大于中轴的数a[left]，这样，a[right-1]和a[left]提供了一个警戒标记，所以不需要检查下标越界的问题。

分析

:最佳的划分是将待排序的序列分成等长的子序列，最佳的状态我们可以使用序列的中间的值，也就是第N/2个数。可是，这很难算出来，并且会明显减慢快速排序的速度。这样的中值的估计可以通过随机选取三个元素并用它们的中值作为枢纽元而得到。事实上，随机性并没有多大的帮助，因此一般的做法是使用左端、右端和中心位置上的三个元素的中值作为枢纽元。显然使用三数中值分割法消除了预排序输入的不好情形，并且减少快排大约14%的比较次数

例子：

初始数组：6 1 8 9 4 3 5 2 7 0

选取三个中间数：

6

1 8 9

4

3 5 2 7

0

对这三个数进行排序：

0

1 8 9

4

3 5 2 7

6

最后中轴与a[right-1]交换：0 1 8 9

7

3 5 2

4

6

代码：

int Median(int *a,int left,int right){
    int midIndex = (left + right)>>1;
    if (a[left] > a[midIndex])
    {
        swap(a[left],a[midIndex]);
    }
    if (a[left] > a[right])
    {
        swap(a[left],a[right]);
    }
    if (a[midIndex] > a[right])
    {
        swap(a[midIndex],a[right]);
    }
    swap(a[midIndex],a[right-1]);
    return a[right-1]; //返回中轴
}

void qSort(int *a,int left,int right){
        //如果需要排序的数据大于3个则使用快速排序
        if (right - left >=3)
        {
            int midIndex = Median(a,left,right);
            int begin = left;
            int end = right - 1;
            while (true){
                while(a[++begin] < midIndex);
                while(a[--end]<midIndex);
                if (begin < end)
                {
                    swap(a[begin],a[end]);
                }
                else{
                    swap(a[begin],a[right -1]);//将枢轴移动到何时位置
                    break;
                }
            }
            qSort(a,left,begin -1);
            qSort(a,begin + 1,right);
        }
        else{
            BubbleSort(a,left,right);//当数据小于3个,直接用冒泡排序
        }//当要排序的数据很少时（小于3个），则不能进行三数取中值，此时直接使用简单的排序（例如冒泡）即可，而且从效率的角度来考虑这也是合理的，因为可以避免函数调用的开销。
    }

当子数组足够小时

改用插入排序方法

一些划分方法的改进

例如三路划分，将数组分成三段，每段的元素分别小于、等于、大于中轴元素。

原文链接：https://blog.csdn.net/weixin_41738030/article/details/89409311