支持向量机的提出是为了解决线性无法分类的问题,想要深入理解就需要从线性分类开始探讨,找到线性分类的优缺点,然后在循序渐进的提出解决方法和思路进而引出支持向量机,在继续深入探讨支持向量机的特点,以及如何分类?分类的原理是什么,支持向量机的难点在哪里?如何解决?带着问题去探讨,这样才符合我们认识事物的规律,本篇讲述就按此进行。
线性分类器:
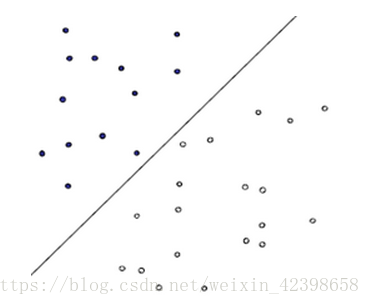
如图二维数据分类的例子,从 图中看,这条分类函数还是可以准确做出判断的,但是这样的一元线性函数只存在一条吗?当然不是,能正确做出判断的函数有很多,如下图:

从图中可以看出这些一元线性函数都可以对此进行分类,但哪个线性分类函数最好呢?如何找出这个最好的线性分类函数呢?
在解释提出的问题之前,先把线性分类函数的一般表达式给出:
还记的Logistic回归中,他的分类函数的表达式是什么样的吗?直接引用博客里的式子:
其中:
为常数
下面就是如何找到最好的分类函数,什么是最好呢?就是分类预测的确信或者准确度达到最高就是最好的了
那么怎么找呢?
找这个分类函数其实就是找最佳的权值向量
和b,怎么找呢?找之前先引入几个概念:
最大边缘超平面(MMH):
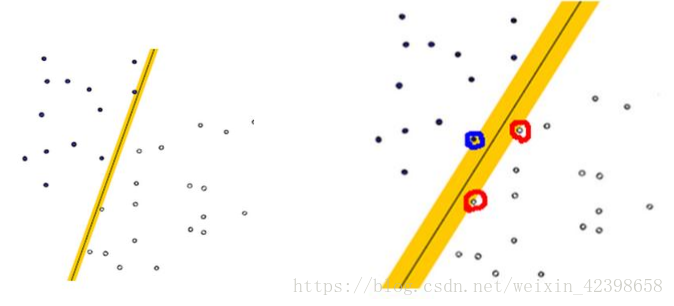
什么是最大边缘超平面呢?大家都知道,在一维中(横轴) 一点可以把数分两类,在二维中,一条直线可以把数据分两类(上面讲的都二维的),在三维中,一个平面可以把数据分两类(大家可以想象空间一个球,过球心的水平面就可以把球分两部分),在四维,五维、六维、、、n维中(我们目前只知道一、二、三维的空间,三维空间可通过平面进行区分空间,更高维度的空间区分他们就叫超平面了,例如 五维空间一般可以通过四维超平面进行分开,n维就是通过n-1维超平面进行区分,下面解释一下最大边界,以二维空间为例,我们知道区分二维平面的是直线,所谓最大边界,例如上图右,蓝色和红色边界的直线(黄色的)称为决策边界,他们分别经过了两边边沿的一个数据点,而这些数据点就称为支持向量点,为什么这样称呼下面会讲解,同时该两条直线之间的空间称为“隔离带”(自称的),如下图:
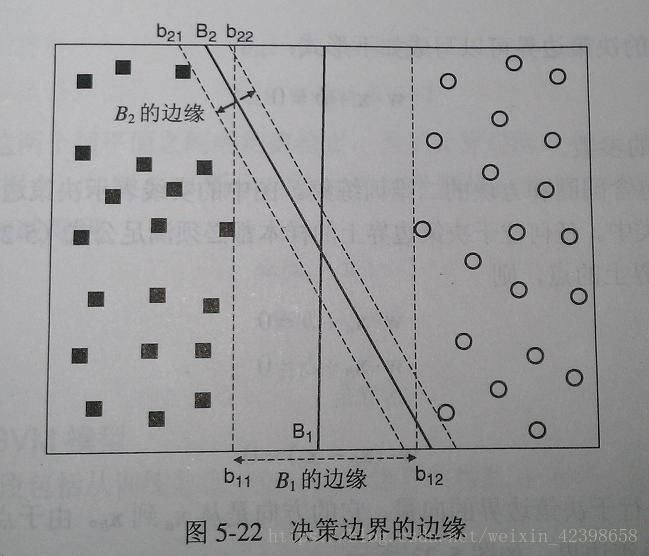
我们可以看到,b11和b12, b21和b22就是最大边缘决策边界(最大边缘超平面),他们分别经过两组数据的第一个点,以此称为决策边界,找到最大边缘分界有什么用呢?其实最优的分类一定就在这之间了,但是如何确定最优的呢?
假如我们找到的决策函数为上图的B1或者B2,大家觉得决策函数应该在哪里最好?直观是不是应该在中间,以B1的边缘为例,那么B1的决策决策函数就在b11和b12中间,因为中间位置到两遍的边缘分界的距离最大,那么他判断正确的确信度就越高,所以‘隔离带’越大越好,即通过求分界线之间的距离建立关系,一旦分界间的距离确定了,那么决策函数就容易求了,因此定义决策超平面(在二维中,是一条线,但是在高维中就是超平面了)如下:
把两边决策边界定义为:
①
②
那么从公式中我们可以看到,在决策边界上的数据点结果是等于1或者-1的(隔离带先假设不存在数据点),其余的应该不等于1或者-1的,结合下图,以二维数据为例,我们知道,下面的图形就是平面图形,边界直线经过坐标系的一二四象限,根据直线和坐标系的位置可知,以①式为例:数据点在①式上的等于1,数据点在它上面的肯定大于1,不信的可以拿个笔计算一下,初中知识了,那么分类方块代表数据总体可以写成这样了:
同理
即分两类了。1代表一类,-1代表一类,同时这两个不等式就是把数据分类了在说简单点,我们后面所要做的所有事情都希望满足这个,为什么呢?因为我们的目的是分类呀,这是最初的目的好吧,进行这一切的操作都是为了更好的分类,你说呢?
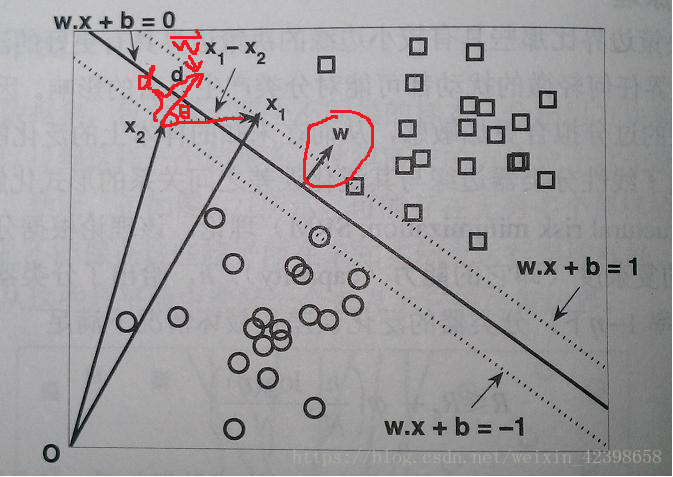
至于为什么是1和-1,那篇文章讲的很详细,我就不啰嗦了,不知道的可以查看一下,需要解释一下为什么边界线通过的点称为支持向量,以二维为例,上图中,我们可以看到x1和x2两个数据点分别是边界线进过的数据点,以0为原点建立直角坐标系,数据x1和x2分别构成的向量为:
和
,,两向量相减得到:
–
=
另外我们知道直线的斜率就是法向量,与直线是垂直的,上图是二维平面,直线的法向量
和直线垂直,同时也是边界线的法向量,因此
和
的內积就可以写出了:
=
內积大家都知道吧,那我们继续,
下面正式推到了,上面是从向量的建立角度进行讲解,为下面的做准备工作。
然而这內积结果为什么等于2呢?可以根据两式相减得到,即两边界方程相减得:即① – ②
又因为
=
(因为都是向量,向量的减法没忘完吧)
所以上式可以写为:
=
其中
为范数,在平面向量里称为模
又因为
其实就是两条边界线的距离d,不懂的可能是夹角
,其实就是法向量
和
中间的夹角,如上图画的,这里大家需要一点向量知识,到这里令:
=
可改写为:
=
所以:
到这里问题就转化了,求d得最大值就可以了。
在这里还有另外一种解决思路:
我们知道平面的两条直线的距离公式为:

如果求边界间的距离,可以直以直接使用该公式即可:
同样可以得到边界线的距离:
这种显得更简洁,但是为什么不直接使用这个呢?因为这个在高维的情况下可能不适用,同时也无法解释什么是支持向量,无法解释支持向量机的本质。
总结一下: 所谓支持向量就是边界超平面经过的数据点,因为这些点才构成边界,因才有支持向量的称呼,但是找边界不是目的,我们希望找到最优的决策超平面,而最优的决策超平面就在决策边界中心位置,而且决策边界间的距离越大越好,即把问题转化为求距离最大问题了。
下面问题是如何求最大距离?有哪些约束条件?下一篇介绍。