文章目录
1. 题目来源
链接:
快乐数
来源:LeetCode
2. 题目说明
编写一个算法来判断一个数是不是“快乐数”。
一个“快乐数”定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是无限循环但始终变不到 1。如果可以变为 1,那么这个数就是快乐数。
示例 :
输入: 19
输出: true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
3. 思维启迪
3.1 单链表
这个有趣的算法思维
涉及到单链表
,下面非常简单的介绍下单链表相关知识:
直观理解单链表这种数据结构,就是把内存中的若干个存储单元,连成了一条链,逻辑结构呢就如下图所示(
这个五颜六色的颜色只是单纯为了好看些…
):

能发现这些像指针一样的小箭头在程序中怎么去实现呢?嗯,没错,就是拿指针实现这些小箭头的指向关系。
链表结构的末尾将指向空地址,即上图的
NULL
。
而单链表存在一条非常关键的性质:
当前节点唯一指向下一个节点。
这个性质就能帮助我们快乐的解决快乐数问题。
3.2 单链表判环
单链表是否存在环是一个非常经典的问题,就如下图所示:
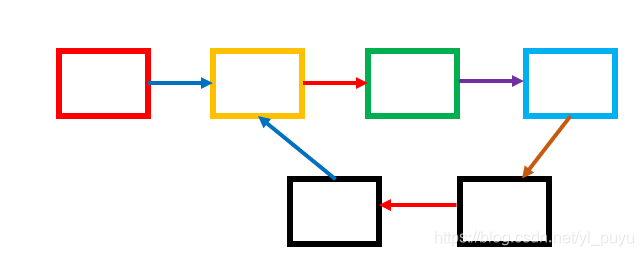
如果让咱们自己来 “肉眼判环”,这个结果就显而易见,但是要把这个扔给计算机来判断,那它可就是 “目光狭窄” 的判断不了了。
其实判断方法比较简单,我们给个生活上的例子,你和博尔特在一个赛道上同时出发,
假设你比博尔特跑的快
,那么当你从后面相遇到博尔特时,可以很自然的给他说一句
“
嗨,我的老伙计,你怎么跑的这么慢,我都超你一圈了~
”
那么就证明了这个赛道是环形赛道。
同理可以引用到单链表中,就是经典的快慢指针解法。我们设置两个指针,一个走得快,一个走得慢,如下图:
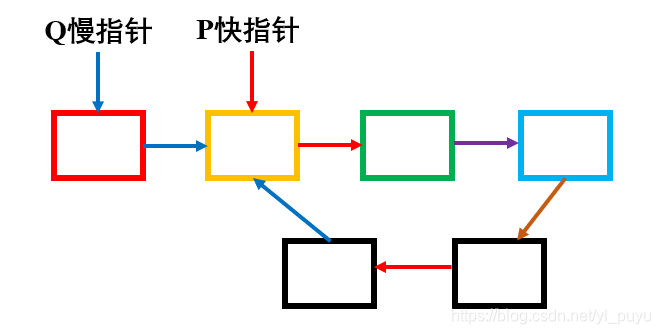
如果
P
、
Q
走着走着相遇了,那么就能证明这个链表就存在环。如果不能相遇的话,那么就肯定是
P
指针首先走到链表的末尾,即指到最后的
NULL
。
3.3 提炼其精华所在
链表中是否有环是一个算法技巧,但是它的价值有限,因为它仅仅只是解决了一个数据结构的问题。
算法和算法思维是绝不等价的两者。
一个算法可能 30 分钟就能学会,但是算法思维是需要长期的锻炼的。下面来看看根据单链表判环能引出那种算法思维。提到思维的话,我们就需要将我们刚刚所掌握的东西做一个泛化的理解:
泛化链表结构
:如果我们
把链表的节点看成问题中的状态
的话,它可以代表问题中的一个数字、一个阶段等等,是很泛化的东西。而链表的唯一指向关系它又代表什么呢?它其实代表着
状态与状态之间是唯一确定转换
的。也就是说从当前状态是唯一确定转换到下一个状态的。
如果问题中存在这种特性,那么我们就能够用链表思维进行概括。
3.4 快乐数与单链表的联系
根据快乐数的转换规则,能得到:

这个转换关系是确定的,即如果当前状态确定了,那么下一个状态就是确定的。那么在思维逻辑上就能将其抽象为链表结构,如下图所示:

这个链表结构就更加清晰了,我们根据题目的意思就将 1 作为链表的结尾即
NULL
。
那么在单链表中一直走不到空地址意味着什么?就意味着链表有环呗。那么这个快乐数问题就被抽象为链表中是否有环的问题。即,
如果这个链表有环那么就不是快乐数,如果链表没环,能指到空地址 1 的话那就说明这个数就是快乐数。
3.5 算法规模,是不是死循环?
从上面我们得到了解决这个问题的算法思维,但是会不会出现这个链表太长了,有上个几千、几万、几十万的链表单元,影响我们找不到结果呢?我们来考虑一下这个算法的规模。
首先,如果输入值为
int
,那么能知道
int
最多也就是一个以 2 开头的 10 位的数字。接着我们来考虑这样一个问题,在
int
数据范围中,哪一个数字
n
它所对应的下一个数字
n
是最大的?
我们能构造得到
1 999 999 999
,那么只有构造出 1 个 1 ,9 个 9 的数字在
int
范围内就是最大的,那么下一个节点时多少呢?根据快乐数的定义能得到
9
2
×
9
+
1
=
730
9^2 \times9 + 1 =730
9
2
×
9
+
1
=
7
3
0
,那么 730 就是在整形范围之内任何一个数字所能映射到的下一个数字都不会超过 730,也就意味着当前所抽象出来的链表结构中节点数目最多不会超过 730 个,如果快指针一次走两步、慢指针一次走一步的话,那么慢指针走的最多,也只不过走了
731
×
2
=
1462
731\times2 = 1462
7
3
1
×
2
=
1
4
6
2
步,而快指针就是走了
731
731
7
3
1
步。
所以至此就证明完了,在整形快乐数中进行单链表判环的操作的话,操作步骤是有限的,就取个整吧,最多最多也就 2000 步了。所以这个方案是高效可行的。
3.6 代码展示
// 执行用时 :0 ms, 在所有 C++ 提交中击败了100.00%的用户
// 内存消耗 :8 MB, 在所有 C++ 提交中击败了89.59%的用户
class Solution {
public:
bool isHappy(int n) {
int p = n, q = getNext(n);
while (q != 1) {
p = getNext(p);
q = getNext(getNext(q));
if (p == q) return false;
}
return true;
}
int getNext(int x) {
int n = 0;
while (x) {
n += (x % 10) * (x % 10);
x /= 10;
}
return n;
}
};
4. 总结
好久没有回到这种做题的快乐感了,或许和做这个快乐数有关吧 😃。其实做这个快乐数题目什么的并不重要,而重要的是需要体会一点:如何从具体的算法推导出算法思维的。这个思维的变换很重要!这也就是真正的
算法之美!