格雷码应用意义及编解码

文章目录

1. 格雷码的应用意义

学过晶体管知识的朋友们都知道，数据位跳变就相当于硬件电路中的晶体管翻转。

许多位同时跳变就相当于多个晶体管同时翻转，会导致电路中出现很大的尖峰电流脉冲，从而导致数据不稳定

。

在一组数的编码中，若任意两个相邻的代码只有一位二进制数不同，则称这种编码为

格雷码

（Gray Code），另外由于最大数与最小数之间也仅一位数不同，即“首尾相连”，因此又称

循环码

或

反射码

。在数字系统中，常要求代码按一定顺序变化。例如，按自然数递增计数，若采用

8421

$8421$

码，则数

0111

$0111$

变到

1000

$1000$

时四位均要变化，而在实际电路中，

4

$4$

位的变化不可能绝对同时发生，则计数中可能出现短暂的其它代码（

1100

$1100$

、

1111

$1111$

等）。在特定情况下可能导致电路状态错误或输入错误。使用格雷码可以避免这种错误。格雷码有多种编码形式。

其重要特征是一个数变为相邻的另一个数时，只有一个数据位发生跳变，由于这种特点，就可以避免电路中出现亚稳态而导致数据错误。简而言之，

格雷码的一位改变特征

减小了电路出错概率，实际很多场合也用到了格雷码。

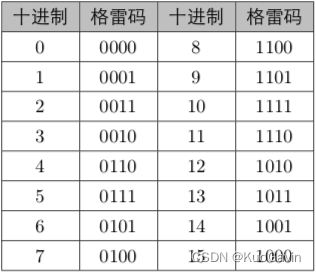
四位格雷码如下图所示：

更多内容，可见百度百科「

格雷码

」。

2. 由自然数编码获得格雷码

leetCode当中关于格雷码的生成有：

89. 格雷编码

、

1238. 循环码排列

2.1 对称法实现

当是

0

$0$

位格雷码时，格雷码序列即为

]

[0]

$[0]$

。

如果我们获取了

−

n-1

$n - 1$

位格雷码序列，并记为

−

G_{n-1}

$G_{n - 1}$

，可以使用它构造获得

n

$n$

位格雷码序列

G_n

$G_{n}$

。具体方法如下：

将
$G_{n-1} G n − 1 复制一份并进行反转，记为 G n − 1 T G_{n-1}^T G n − 1 T ；$
将
$G_{n-1}^T G n − 1 T 中每个元素的第 n − 1 n-1 n − 1 个二进制位均从 0 0 0 变为 1 1 1 ，得到 ( G n − 1 T ) ′ (G_{n-1}^T)’ ( G n − 1 T ) ′ 。这里最低的二进制位为第 0 0 0 个二进制位；$
将
$G_{n-1} G n − 1 和 ( G n − 1 T ) ′ (G_{n-1}^T)’ ( G n − 1 T ) ′ 进行拼接，得到 G n G_n G n 。$

证明如下：

由于
$G_{n-1} G n − 1 是 [ 0 , 2 ( − 1 ) [0, 2^{(-1}) [ 0 , 2 ( − 1 ) 的排列，那么其中每个元素的第 n − 1 n-1 n − 1 个二进制位都是 0 0 0 。进而， ( G n − 1 T ) ′ (G_{n-1}^T)’ ( G n − 1 T ) ′ 是 [ 2 n − 1 , 2 n ) [2^{n-1}, 2^{n}) [ 2 n − 1 , 2 n ) 的排列，所以 G n = G n − 1 + ( G n − 1 T ) ′ G_n=G_{n-1}+(G_{n-1}^T)’ G n = G n − 1 + ( G n − 1 T ) ′ 就是 [ 0 , 2 n ) [0,2^n) [ 0 , 2 n ) 的排列；$
对于
$G_{n-1} G n − 1 和 ( G n − 1 T ) ′ (G_{n-1}^T)’ ( G n − 1 T ) ′ 的内部，每对相邻整数的二进制恰好有一位不同。对于 G n − 1 G_{n-1} G n − 1 最后一个数和 ( G n − 1 T ) ′ (G_{n-1}^T)’ ( G n − 1 T ) ′ 第一个数，它们只有第 n − 1 n-1 n − 1 个二进制位不同。对于 G n − 1 G_{n-1} G n − 1 第一个数和 ( G n − 1 T ) ′ (G_{n-1}^T)’ ( G n − 1 T ) ′ 最后一个数，它们也仅有第 n − 1 n-1 n − 1 个二进制位不同。$

因此，

G_n

$G_{n}$

就是满足要求的

n

$n$

位格雷码序列。对应的cpp代码为：

class Solution {
public:
    vector<int> grayCode(int n) {
        vector<int> ans;
        ans.push_back(0);
        for (int i = 1; i <=n; ++i) {
            int t = ans.size();
            for (int j = t-1; j >= 0; --j) {
                //ans.push_back(ans[j] + (1 << (i-1)));
                //这里+，|运算等效，因为0|A=A，且这里是按位或
                ans.push_back(ans[j] | (1 << (i-1)));
            }
        }
        return ans;
    }
};

2.2 公式法实现

也可以由公式直接求出，第

(

≥

)

i(i\ge0)

$i (i \geq 0)$

个格雷码为：

⊕

⌊

⌋

g_i=i\oplus\lfloor\frac{i}{2}\rfloor

$g_{i} = i \oplus ⌊ \frac{i}{2} ⌋$

其中

\oplus

$\oplus$

表示按位异或运算，正确性证明如下：

当
$\lfloor\frac{i}{2}\rfloor ⌊ 2 i ⌋ 和 ⌊ i + 1 2 ⌋ \lfloor\frac{i+1}{2}\rfloor ⌊ 2 i + 1 ⌋ 相等，进而异或之后 g i g_i g i 和 g i + 1 g_{i+1} g i + 1 也只有最低的一个二进制位不同；$
当
i

i

$i$

为奇数时，我们记

i

$i$

的二进制表示为

⋯

01

⋯

11

)

2

(⋯01⋯11)_2

$(\dots 01 \dots 11)_{2}$

，

+

1

i+1

$i + 1$

的二进制表示为

⋯

10

⋯

00

)

2

(⋯10⋯00)_2

$(\dots 10 \dots 00)_{2}$

，即：
- 那么
  $\lfloor\frac{i}{2}\rfloor ⌊ 2 i ⌋ 和 ⌊ i + 1 2 ⌋ \lfloor\frac{i+1}{2}\rfloor ⌊ 2 i + 1 ⌋ 的二进制表示分别为 ( ⋯ 01 ⋯ 1 ) 2 (⋯01⋯1)_2 ( ⋯ 01 ⋯ 1 ) 2 和 ( ⋯ 10 ⋯ 0 ) 2 (⋯10⋯0)_2 ( ⋯ 10 ⋯ 0 ) 2 ，进而有： g i = ( ⋯ 01 ⋯ 11 ) 2 ⊕ ( ⋯ 10 ⋯ 0 ) 2 = ( ⋯ 010 ⋯ 0 ) 2 g_i=(⋯01⋯11)_2\oplus(⋯10⋯0)_2=(⋯010⋯0)_2 g i = ( ⋯ 01 ⋯ 11 ) 2 ⊕ ( ⋯ 10 ⋯ 0 ) 2 = ( ⋯ 010 ⋯ 0 ) 2 ，以及： g i + 1 = ( ⋯ 10 ⋯ 00 ) 2 ⊕ ( ⋯ 10 ⋯ 0 ) 2 = ( ⋯ 110 ⋯ 0 ) 2 g_{i+1}=(⋯10⋯00)_2\oplus(⋯10⋯0)_2=(⋯110⋯0)_2 g i + 1 = ( ⋯ 10 ⋯ 00 ) 2 ⊕ ( ⋯ 10 ⋯ 0 ) 2 = ( ⋯ 110 ⋯ 0 ) 2 ，也只有一个二进制位不同。$
- 注意到，当我们在表示
  $(⋯10⋯00)_2 ( ⋯ 10 ⋯ 00 ) 2 ，默认了其二进制表示的低位至少有两个 0 0 0 。事实上，当 i + 1 i+1 i + 1 是 2 2 2 的倍数而不是 4 4 4 的倍数时，结论相同。$

class Solution {
public:
    vector<int> grayCode(int n) {
        vector<int> ret(1 << n);
        for (int i = 0; i < ret.size(); ++i) 
            ret[i] = (i >> 1) ^ i;
        return ret;
    }
};

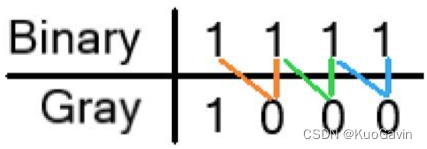
也即二进制到格雷码转换的固定规律为：

格雷码中的最高有效位（最左边）等同于二进制数中相应的最高有效位;
从左到右，加上每一对相邻的二进制编码位，从而得到下一个格雷码位，舍去进位。

3. 由格雷码解码获得自然数

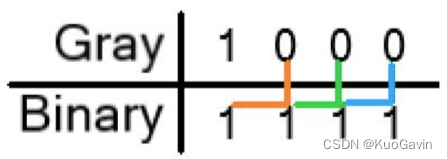
格雷码到二进制转换的固定规律为：

二进制码的最高有效位（最左边）等同于格雷码中相应的最高有效位。
将所产生的每个二进制码位加下一个相邻位置的格雷码位，从而得到下一个二进制位。舍去进位。

/*解码模板 */
#include<math.h>		// log对数函数需要用到的头文件
#include <iostream>
using namespace std;
 
int gray_decode(int num) {
	int head;
	if (!num) return 0;
	head = 1 << int(log(num) / log(2));	//C++没有直接以2为底的对数，我们创造一个以2为底的对数
   return head + gray_decode((num^head) ^ (head>>1));
}

原文链接：https://blog.csdn.net/yueguangmuyu/article/details/129176091