关于欧几里得算法，贝祖等式，扩展欧几里得算法，

Wikipedia的解释

非常非常详细了。

另外，看了好多别人优秀的总结，我认为最详尽的就是

ACM之家

的总结。

这里自己再总结一次…实际上就是把别人总结的，我认为有助于自己理解的内容copy过来，再加上几句自己的理解。

本文包括：

欧几里德算法递归实现
欧几里德算法非递归实现
贝祖等式
扩展欧几里德算法递归实现
扩展欧几里德算法非递归实现

#欧几里得算法

欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数 gcd(a,b)。基本算法：设

a = qb + r

，其中a，b，q，r都是整数，则 gcd(a,b) = gcd(b,r)，即 gcd(a,b) = gcd(b,a%b)。

证明：

a = qb + r

如果 r = 0，那么 a 是 b 的倍数，此时显然 b 是 a 和 b 的最大公约数。

如果 r ≠ 0，任何整除 a 和 b 的数必定整除 a – qb = r，而且任何同时整除 b 和 r 的数必定整除 qb + r = a，所以 a 和 b 的公约数集合与 b 和r 的公约数集合是相同的。特别的，a 和 b 的最大公约数是相同的。

递归实现：

int gcd(int a, int b)
{
	return b == 0 ? a : gcd(b, a%b);
}

非递归实现：

int gcd(int a, int b)
{
	while(b)
	{
		int t = b;
		b = a % b;
		a = t;
	}
	return a;
}

贝祖等式

在数论中，裴蜀等式（英语：Bézout’s identity）或

贝祖定理

（Bézout’s lemma）是一个关于最大公约数（或最大公约式）的定理。裴蜀定理得名于法国数学家艾蒂安·裴蜀，说明了对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性丢番图方程（称为裴蜀等式）：

ax + by = m

有整数解时当且仅当m是d的倍数。

裴蜀等式有解时必然有无穷多个整数解，每组解x、y都称为裴蜀数，可用扩展欧几里得算法(Extended Euclidean algorithm)求得。

例如，12和42的最大公因数是6，则方程12x+42y=6有解。事实上有(-3)×12 + 1×42 = 6及4×12 + (-1)×42 = 6。

特别来说，方程 ax+by=1 有整数解当且仅当整数a和b互素。

裴蜀等式也可以用来给最大公约数定义： d其实就是最小的可以写成ax+by形式的正整数。(这个定义的本质是整环中“理想”的概念。因此对于多项式整环也有相应的裴蜀定理。)

证明:

如果

a

$a$

和

b

$b$

中有一个是 0，比如

a = 0

$a = 0$

，那么它们两个的最大公约数是

b

$b$

。这时裴蜀等式变成

\displaystyle by=m

$b y = m$

，它有整数解 (x,y) 当且仅当

m

$m$

是

b

$b$

的倍数，而且有解时必然有无穷多个解，因为

x

$x$

可以是任何整数。定理成立。

以下设 a和 b 都不为0。

设

{

;

(

;

)

∈

}

A=\{xa+yb; (x;y)\in \mathbb{Z } ^{2}\}

$A = {x a + y b; (x; y) \in Z^{2}}$

，下面证明A中的最小正元素是 a 与 b 的最大公约数。

首先，

∩

∗

A\cap \mathbb{N} ^{*}

$A \cap N^{*}$

不是空集（至少包含

∣

|a|

$∣ a ∣$

和

∣

|b|

$∣ b ∣$

），因此由于自然数集合是良序的，

A

$A$

中存在

最小正元素

d_{0}=x_{0}a+y_{0}b

$d_{0} = x_{0} a + y_{0} b$

。考虑

A

$A$

中任意一个

正

元素

（

）

p（=x_{1}a+y_{1}b）

$p （ = x_{1} a + y_{1} b ）$

对

d_{0}

$d_{0}$

的带余除法：设

p=qd_{0}+r

$p = q d_{0} + r$

，其中

q

$q$

为正整数，

≤

0\leq r<d_{0}

$0 \leq r < d_{0}$

。但是

−

(

)

∈

r=p-qd_{0}=x_{1}a+y_{1}b-q(x_{0}a+y_{0}b)\in A

$r = p - q d_{0} = x_{1} a + y_{1} b - q (x_{0} a + y_{0} b) \in A$

而

0

d_{0}

$d_{0}$

已经是集合

A

$A$

中最小的正元素了，又

≤

r

<

d

0

0\leq r<d_{0}

$0 \leq r < d_{0}$

,所以

=

0

r = 0

$r = 0$

。

因此

∣

d_{0}\ |\ p

$d_{0} ∣ p$

。也就是说，A中任意一个正元素p都是

d_{0}

$d_{0}$

的倍数，特别地：

∣

、

∣

d_{0}\ |\ a、d_{0}\ |\ b

$d_{0} ∣ a 、 d_{0} ∣ b$

。因此

d_{0}

$d_{0}$

是

a

$a$

和

b

$b$

的公约数。

另一方面，对 a 和 b 的任意正公约数

d

$d$

，设

、

a=kd、 b=ld

$a = k d 、 b = l d$

，那么

(

)

d_{0}=x_{0}a+y_{0}b=(x_{0}k+y_{0}l)d

$d_{0} = x_{0} a + y_{0} b = (x_{0} k + y_{0} l) d$

≥

x_{0}k+y_{0}l \geq 1

$x_{0} k + y_{0} l \geq 1$

,因此

∣

d\ |\ d_{0}

$d ∣ d_{0}$

。所以

d_{0}

$d_{0}$

是

a

$a$

和

b

$b$

的最大公约数。

在方程

ax+by=m

$a x + b y = m$

中，如果

m=m_{0}d_{0}

$m = m_{0} d_{0}$

，那么方程显然有无穷多个解：

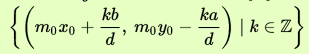
这里写图片描述

相反的，如果

ax+by=m

$a x + b y = m$

有整数解，那么

∣

∈

|m|\in A

$∣ m ∣ \in A$

，于是由前可知

∣

d_{0}\ |\ |m|

$d_{0} ∣ ∣ m ∣$

（即

∣

d_{0}\ |\ m

$d_{0} ∣ m$

）。

m=1时，方程有解当且仅当a、b互质。方程有解时，解的集合是

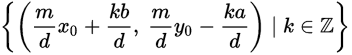
这里写图片描述

其中

)

(x_{0},y_{0})

$(x_{0}, y_{0})$

是方程ax+by=d的一个解，可由辗转相除法得到。

所有解中，有且仅有一个解(x,y) 满足

≤

，

−

≤

-b\leq x\leq b，-a\leq y\leq a

$- b \leq x \leq b ， - a \leq y \leq a$

。

#扩展欧几里得算法

扩展欧几里得算法就是在求

a,b

$a, b$

的最大公约数

(

)

m = gcd(a,b)

$m = g c d (a, b)$

的同时，求出贝祖等式***ax + by = m***的一个解

)

(x,y)

$(x, y)$

。

##扩展欧几里得算法的递归实现：

有两个数

a,b

$a, b$

，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到

(

)

ax+by=gcd(a,b)

$a x + b y = g c d (a, b)$

的整数解。

先来看下这个几乎所有总结扩展欧几里得算法的帖子中都会用到的例子

（可能出自wikipedia，毕竟wikipedia上也是用的这个栗子）：

用类似辗转相除法，求二元一次不定方程47x+30y=1的整数解。
47=30*1+17
30=17*1+13
17=13*1+4
13=4*3+1
然后把它们改写成“余数等于”的形式

17=47*1+30*(-1) //式1
13=30*1+17*(-1) //式2
4=17*1+13*(-1) //式3
1=13*1+4*(-3)
然后把它们“倒回去”

1=13*1+4*(-3) //应用式3
1=13*1+[17*1+13*(-1)]*(-3)
1=13*4+17*(-3) //应用式2
1=[30*1+17*(-1)]*4+17*(-3)
1=30*4+17*(-7) //应用式1
1=30*4+[47*1+30*(-1)]*(-7)
1=30*11+47*(-7)
得解x=-7, y=11。

这些式子自己手写一遍才能理解的更清楚。

这个“倒回去”的过程对应的就是代码中递归向上返回的过程。现在的问题就是要找出这个可以倒回去的递推关系。

参照

ACM之家

中的证明：

(

)

ax + by = gcd(a,b)

$a x + b y = g c d (a, b)$

   设：a>b。
　　推理1，显然当 b=0，gcd（a，b）=a。此时 x=1，y=0;//推理1
　　推理2，ab!=0 时
　　设 ax1+by1=gcd(a,b);
　　bx2+(a mod b)y2=gcd(b,a mod b);
　　根据朴素的欧几里德原理有 gcd(a,b)=gcd(b,a mod b);
　　则:ax1+by1=bx2+(a mod b)y2;
　　即:ax1+by1=bx2+(a-(a/b)*b)y2=ay2+bx2-(a/b)*by2;
　　根据恒等定理得：x1=y2 ,y1=x2-(a/b)*y2;//推理2
　　这样我们就得到了求解 x1,y1 的方法：x1，y1 的值基于 x2，y2.
   上面的思想是以递归定义的，因为 gcd 不断的递归求解一定会有个时候 b=0，所以递归可以结束。

这样我们就找到了递推关系：

$x1=y2; $

−

(

)

∗

;

y1=x2-(a/b)*y2;

$y 1 = x 2 - (a / b) * y 2;$

递推的终止条件再上面也已经给出：

，

（

，

）

。

此

时

，

;

当 b=0，gcd（a，b）=a。此时 x=1，y=0;

$当 b = 0 ， g c d （ a ， b ） = a 。此时 x = 1 ， y = 0;$

由此我们可以得到递归的扩展欧几里得算法的代码：

int exgcd(int a, int b, int &x, int &y)
{
	if(b == 0)
	{//推理1，终止条件
		x = 1;
		y = 0;
		return a;
	}
	int r = exgcd(b, a%b, x, y);
	//先得到更底层的x2,y2,再根据计算好的x2,y2计算x1，y1。
	//推理2，递推关系
	int t = y;
	y = x - (a/b) * y;
	x = t;
	return r;
}

比如上面的 47x+30y=1 的例子，exgcd() 要求出 gcd(47, 30)，同时得到一组（x，y）的解。

 用一个方便我自己理解的方式，把求解的过程写出来好了。这里的大括号"{}"里面不是函数体，"{"表示一层递归调用的开始,"}"表示该层递归的结束。 
 exgcd(47, 30, x, y)
 {
	 r = exgcd(30, 17，x, y)
	 {
		 r = exgcd(17, 13, x, y)
		 {
			 r = exgcd(13, 4, x, y)
			 {
				 r = exgcd(4, 1, x, y)
				 {
					 r = exgcd(1, 0, x, y)
					 {
						 x = 1; 
						 y = 0;
						 return 1;
					 }
					 t = y = 0;
					 y = x - (4/1) * y = 1;
					 x = t = 0;
					 return r = 1; 
				 }
				 t = 1;
				 y = 0 - (13/4) * 1 = -3;
				 x = 1;
				 return 1;
			 }
			 t = -3;
			 y = 1 - (17/13) * (-3) = 4;
			 x = -3;
			 return 1;
		 }
		 t = 4;
		 y = -3 - (30/17) * 4 = -7;
		 x = 4;
		 return 1;
	 }
	 t = -7;
	 y = 4 - (47/30) * (-7) = 11;
	 x = -7;
	 return 1;
 }
 最后的结果:
 r = exgcd(47,30,x,y) = 1;
 x = -7;
 y = 11;

##扩展欧几里得算法的非递归实现！

非递归的算法明显就要比递归的复杂到不知哪里去啦，可能是智商捉急，这个非递归的扩展欧几里得算法我理解了好久好久。

让我决定彻底弄清楚扩展欧几里得算法的原因，正是《计算机程序设计艺术》1.2数学归纳法中介绍的算法E(推广的欧几里得算法)。用数学归纳法我也能归出来这个算法是正确的，数学归纳法简洁优美，但是还是需要得到递推关系我才算真正理解这个算法。

百度没找到完整的非递归扩展欧几里得算法递推关系的推到过程，自己推了半天推不动。

http://anh.cs.luc.edu/331/notes/xgcd.pdf

http://math.cmu.edu/~bkell/21110-2010s/extended-euclidean.html

还好找到两篇英文的，两篇一起看效果更佳！找到这两篇简直感动到cry，太详细了！

算法

E

$E$

(推广的欧几里得算法). 给定两个正整数m和n，计算他们的最大公因数d，并计算两个未必为正数的整数 a 和 b, 使得

am + bn = d

$a m + b n = d$

.

E1.

$E 1 .$

[初始化.] 置

′

←

′

←

a’ \leftarrow b \leftarrow 1, a \leftarrow b’ \leftarrow 0, c \leftarrow m, d \leftarrow n.

$a^{'} \leftarrow b \leftarrow 1, a \leftarrow b^{'} \leftarrow 0, c \leftarrow m, d \leftarrow n .$

E2.

$E 2 .$

[除法.] 令

q

$q$

和

r

$r$

分别是用

d

$d$

除

c

$c$

所得的商和余数. （我们有

c = qd + r

$c = q d + r$

和

≤

0 \leq r < d.

$0 \leq r < d .$

）

E3.

$E 3 .$

[余数为0？] 如果

r = 0

$r = 0$

，算法终止，此时有

am + bn = d

$a m + b n = d$

, 正如所求.

E4.

$E 4 .$

[循环.] 置

←

′

←

−

←

′

←

−

c \leftarrow d , d \leftarrow r , t \leftarrow a’ , a’ \leftarrow a , a \leftarrow t – qa , t \leftarrow b’ , b’ \leftarrow b , b \leftarrow t – qb

$c \leftarrow d, d \leftarrow r, t \leftarrow a^{'}, a^{'} \leftarrow a, a \leftarrow t - q a, t \leftarrow b^{'}, b^{'} \leftarrow b, b \leftarrow t - q b$

，然后返回

E2.

$E 2 .$

┃

假定 m = 1769 ， n = 551, 我们相继得到：


1	0	0	1	1769	551	3	116
0	1	1	-3	551	116	4	87
1	-4	-3	13	116	87	1	29
-4	5	13	-16	87	29	3	0

答案是正确的： 5×1769 – 16×551 = 8845 – 8816 = 29, 这是1769和551的最大公因数。《计算机程序设计艺术》用的数学归纳法证明。

首先我们发现等式：

′

a’m + b’n = c, am + bn = d

$a^{'} m + b^{'} n = c, a m + b n = d$

在步骤

E2

$E 2$

执行后总是成立。 (1)

 证明(1):
  算法首次转到E2时，由上表，显然等式成立。
  步骤 E2，E3 并不会改变等式的正确性。
  所以只需要证明步骤 E4 不改变他们的正确性就可以了。
  
  执行 E4 之前，
	  a'm + b'n = c    (*)
	  am + bn = d      (**)
  成立。
  a'm + b'n = c = qd + r;
  a'm + b'n - q(am + bn) = r;
  (a' - qa)m + (b' - qb)n = r  (***)
  
  执行 E4 之后，c←d, d←r, t←a', a'←a, a←t-qa, t←b', b'←b, b←t-qb;
  所以
  (**)变为 a' + b' = c
  (***)变为 am + bn = d
  所以步骤 E4 不改变等式的正确性，得证。

现在我们对n归纳，证明算法

E

$E$

是正确的：如果

m

$m$

是

n

$n$

的倍数，算法显然能够正确执行，因为在第一次达到

E3

$E 3$

的时候就立即完成了。当

n = 1

$n = 1$

时这种情况总是出现，剩下的情况仅是

n > 1

$n > 1$

且

m

$m$

不是

n

$n$

的倍数。在这种情况下，算法在第一次执行后置

←

c \leftarrow n

$c \leftarrow n$

和

←

d \leftarrow r

$d \leftarrow r$

，并且由于

←

r \leftarrow n

$r \leftarrow n$

,

按归纳法可以假设

,

d

$d$

的最终值是

n

$n$

和

r

$r$

的最大公因数。根据上文欧几里得算法的论证，数偶

}

\{m,n\}

${m, n}$

和

}

\{n,r\}

${n, r}$

具有相同的公因数，特别的，它们具有相同的最大公因数。因此

d

$d$

是

m

$m$

和

n

$n$

的最大公因数，而且由(1)式，

am + bn = d

$a m + b n = d$

。

看完了优美的数学归纳法证明，我们来找找

′

a’m + b’n = c, am + bn = d

$a^{'} m + b^{'} n = c, a m + b n = d$

的递推公式：

首先我们发现

′

a’m + b’n = c, am + bn = d

$a^{'} m + b^{'} n = c, a m + b n = d$

这两个式子是等价的，只是同一个式子的不同阶段。

′

a’m + b’n = c

$a^{'} m + b^{'} n = c$

保存了

am + bn = d

$a m + b n = d$

的上一个阶段。所以我们只需要得到其中一个的递推公式就可以了。

实际上

′

a’

$a^{'}$

只是保存了

a

$a$

之前的一个阶段。

下面我们求解

am + bn = d

$a m + b n = d$

的递推公式。

如果给上表标上序号：

序号							余数等于
1	0	1	1769	551	3	116	116 = m + (-3)n
2	1	-3	551	116	4	87	87 = -4m + 13n
3	-4	13	116	87	1	29	29 = 5m +(-16)n
4	5	-16	87	29	3	0

第

i

$i$

行的变量分别为

a_{i}, b_{i}, c_{i}, d_{i}, q_{i}, r_{i}

$a_{i}, b_{i}, c_{i}, d_{i}, q_{i}, r_{i}$

。

再 gcd() 的过程中，我们会得到一系列的余数，但我们不仅仅想得到这些余数的序列，我们还想得到

a_{i}m + b_{i}n = d_{i}

$a_{i} m + b_{i} n = d_{i}$

这样的等式。

因为

−

d_{i} = r_{i-1}

$d_{i} = r_{i - 1}$

，所以

d

$d$

序列本身就是

r

$r$

的序列。从上表可以清楚的看到这二者之间的关系。

第一行：

a_{1} = 0, b_{1} = 1

$a_{1} = 0, b_{1} = 1$

0×1769 + 1×551 = 551 初始条件是成立的，即

a_{1}m + b_{1}n = d_{1}

$a_{1} m + b_{1} n = d_{1}$

;

第二行：由第一行的 1769 = 3×551 + 116 ,把余数116表示为 116 = 1×1769 + (-3)×551 = m + (-3)n, 我们注意到第一行的余数

r_{1}

$r_{1}$

等于第二行的

d_{2}

$d_{2}$

所以

−

a_{2} = 1, b_{2} = -3

$a_{2} = 1, b_{2} = - 3$

,

a_{2}m + b_{2}n = r_{1} = d_{2}

$a_{2} m + b_{2} n = r_{1} = d_{2}$

第三行：由第二行的 551 = 4×116 +87，把余数87表示为 87 = 551 + (-4)×116, 其中551 = n, 而116已经求得为m+(-3)n, 所以 87 = n + (-4)(m+(-3)n) = -4m + 13n ，即

−

a_{3} = -4, b_{3} = 13

$a_{3} = - 4, b_{3} = 13$

,

a_{3}m + b_{3}n = r_{2} = d_{3}

$a_{3} m + b_{3} n = r_{2} = d_{3}$

;

第四行：由第三行的 116 = 1×87 + 29，把余数29表示为 29 = 116 + (-1)×87 = (m + (-3)n) + (-1)(-4m + 13n) = 5m +(-16)n，所以

−

a_{4} = 5, b_{4} = -16

$a_{4} = 5, b_{4} = - 16$

，

a_{4}m + b_{4}n = r_{3} = d_{4}

$a_{4} m + b_{4} n = r_{3} = d_{4}$

;

第五行：由第4行的 87 = 3×29 ，

r_{4} = 0

$r_{4} = 0$

，算法终止，

d_{4}

$d_{4}$

即为最大公约数，

a_{4}, b_{4}

$a_{4}, b_{4}$

即为求得的满足

(

)

am+bn=gcd(m,n)

$a m + b n = g c d (m, n)$

的

a, b

$a, b$

。

我们发现 :

−

(

−

)

−

(

−

)

d_{i} = r_{i-1} = c_{i-1} – q_{i-1}d_{i-1} = d_{i-2} – q_{i-1}d_{i-1} = (a_{i-2}m + b_{i-2}n) – q_{i-1}(a_{i-1}m + b_{i-1}n)

$d_{i} = r_{i - 1} = c_{i - 1} - q_{i - 1} d_{i - 1} = d_{i - 2} - q_{i - 1} d_{i - 1} = (a_{i - 2} m + b_{i - 2} n) - q_{i - 1} (a_{i - 1} m + b_{i - 1} n)$

(

−

)

(

−

)

= (a_{i-2} – q_{i-1}a_{i-1})m + (b_{i-2} – q_{i-1}b_{i-1})n

$= (a_{i - 2} - q_{i - 1} a_{i - 1}) m + (b_{i - 2} - q_{i - 1} b_{i - 1}) n$

又

d_{i} = a_{i}m + b_{i}n

$d_{i} = a_{i} m + b_{i} n$

所以

−

a_{i} = a_{i-2} – q_{i-1}a_{i-1}

$a_{i} = a_{i - 2} - q_{i - 1} a_{i - 1}$

;

−

b_{i} = b_{i-2} – q_{i-1}b_{i-1}

$b_{i} = b_{i - 2} - q_{i - 1} b_{i - 1}$

;

实际上，这里的

−

a_{i-2}, b_{i-2}

$a_{i - 2}, b_{i - 2}$

就是

′

a’_{i}, b’_{i}

$a_{i}^{'}, b_{i}^{'}$

。

于是，我们就找到了

am + bn = d

$a m + b n = d$

的系数

a

$a$

和

b

$b$

的递推公式。

最后，给出非递归的C++代码：

int exgcd(int m, int n, int &x, int &y) {
    if (n == 0) {
        x = 1; y = 0;
        return m;
    }
    int a, a1, b, b1, c, d, q, r, t;
    a1 = b = 1;
    a = b1 = 0;
    c = m; d = n;

    q = c/d; r = c%d;
    while (r) {
        c = d;
        d = r;
        t = a1;
        a1 = a;
        a = t - q * a;
        t = b1;
        b1 = b;
        b = t - q * b;

        q = c/d;
        r = c%d;
    }
    x = a; y = b;
    return d;
}

原文链接：https://blog.csdn.net/yoer77/article/details/69568676

贝祖等式

你可能也喜欢