参考来源：

【OpenMMLab 公开课】图像分类与 MMClassification

前面一篇博文

总结了传统图像分类算法的设计思路，以及后来的基于CNN的分类网络的演化过程，从AlexNet到GoogleNet，然后是ResNet、MobileNet等，以及后来的EfficientNet和注意力机制。本文总结分类模型具体的训练过程以及PyTorch框架

目录

1. 图像分类模型训练

1.1 交叉熵损失函数

1.2 训练CNN的困难之处

1.3 梯度下降算法及其改进

1.4 学习率设置策略

1.5 自适应梯度算法

1.6 权重初始化策略

1.7 防止过拟合的策略

1.8 数据增广策略

1.9 Batch Normalization

1.10 总结

2. PyTorch框架简介

2.1 PyTorch的基本模块

2.2 数值计算库torch

2.3 自动求导torch.autograd

2.4 函数库torch.nn.functional

2.5 通用模型封装torch.nn.Module

2.6 优化器torch.optim

2.7 数据工具torch.utils.data

1. 图像分类模型训练

1.1 交叉熵损失函数

• 分类任务的神经网络会输出K维类别向量P，y为真实类别标签，交叉熵损失为向量P的某个真实类别维度的概率值取对数然后取负号。减函数，也就是Py越大，损失越小

1.2 训练CNN的困难之处

• 
  数据量大，计算量大
  
  ：例如在ImageNet数据集上训练AlexNet，有100万张图片，大约6000万个参数
• 
  损失函数复杂度高（高维非凸函数）
  
• 
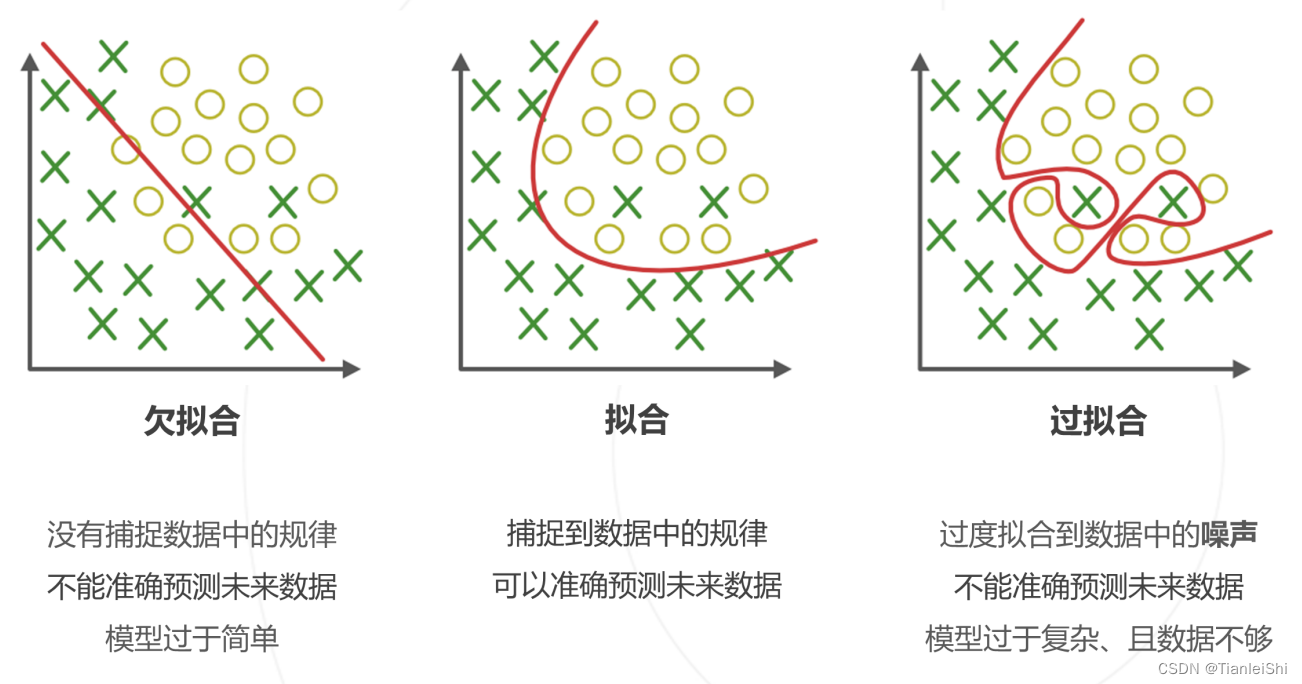
  模型复杂度高，过拟合现象
  

1.3 梯度下降算法及其改进

• 
  梯度下降算法
  
  ：给定数据集，模型和损失函数。首先初始化模型参数，设置学习率，通过前向传播，反向传播计算梯度，更新参数，直至收敛。
• 
  随机梯度下降算法
  
  ：（梯度下降每走一步就只要在整个数据集上计算全部参数，显然不可能，这就出现了SCD）
  • 每次迭代随机选取样本子集（称为批Mini Batch），近似计算损失函数的梯度
• 
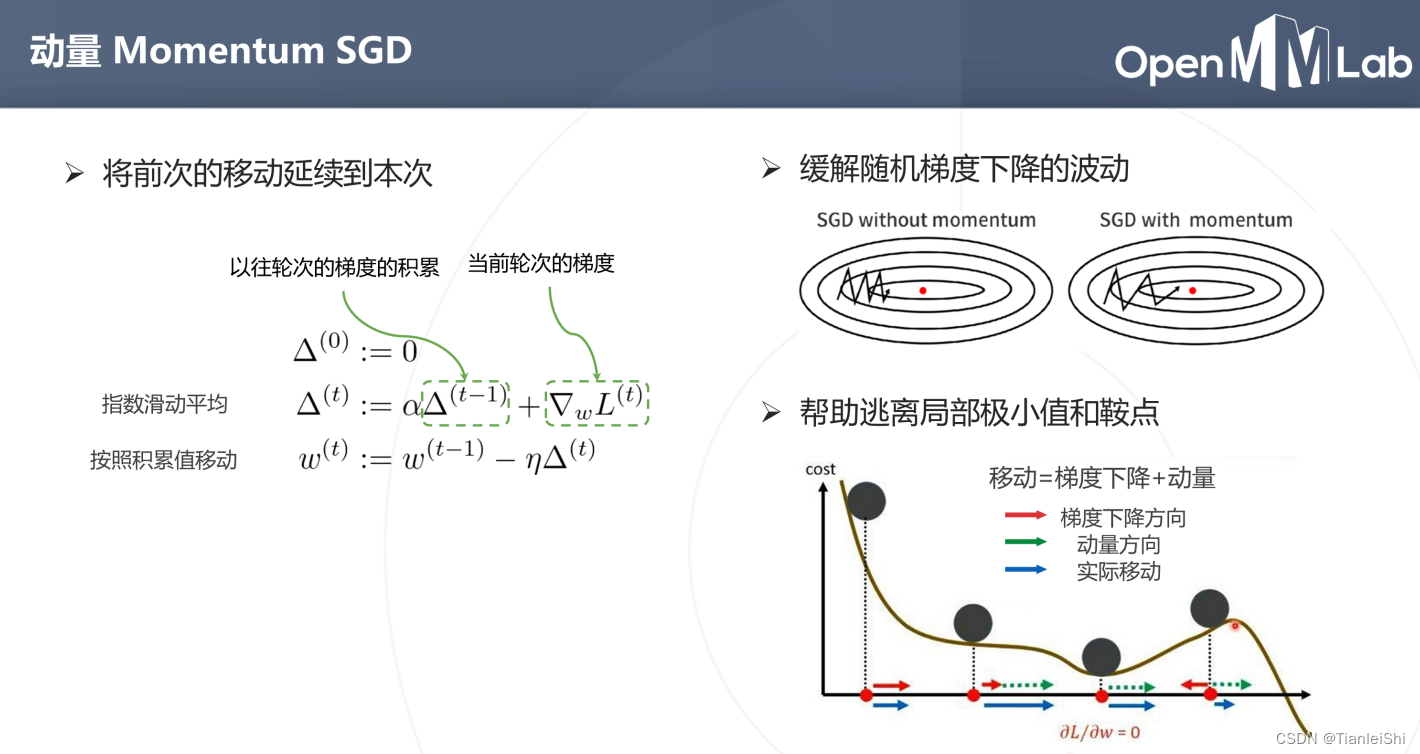
  动量Momentum SGD
  
  ：（SGD下降波动比较大，为了减小误差，不让梯度乱走。就考虑把在以往数据上计算的梯度移动延续到这次移动，引入了动量）
  • 不是按照梯度去移动，而是按照累计值移动

1.4 学习率设置策略

• 学习率退火策略：最常用，在训练初始阶段使用较大的学习率，损失函数稳定后下降学习率（按步长下降，按比例下降，按倒数下降等）

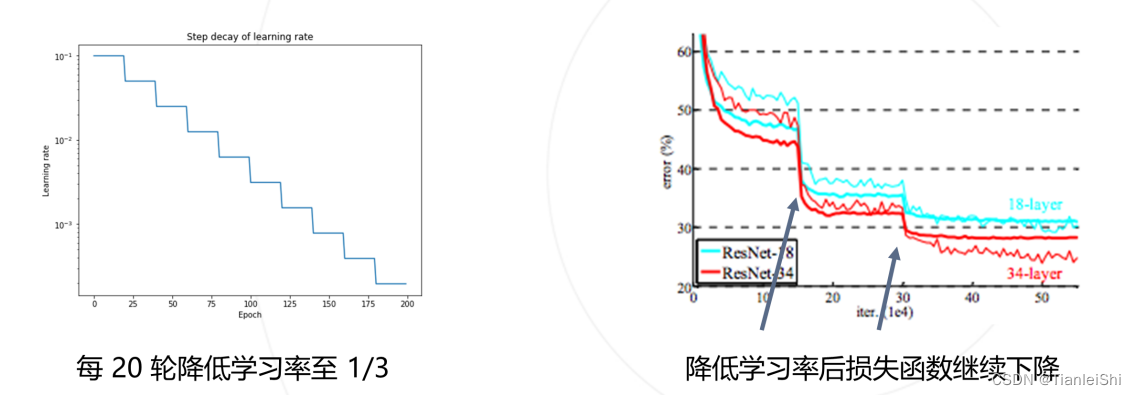
• 学习率升温（Warmup）：在训练前几轮学习率逐渐上升，指导预设的学习率，以稳定训练的初始阶段，可以线性上升等。与退火结合使用
• 当然，学习率这么设置的话仍然存在一个问题就是：所有的参数都按照同一个学习率下降，有时候并不希望这样，这就出现了自适应梯度算法

1.5 自适应梯度算法

• 不同梯度需要不同的学习率，根据梯度的幅度自动调整学习率

1.6 权重初始化策略

• 针对卷积层和全连接层，初始化连接权重W和偏置
• 随机初始化方法：
  • 朴素方法：依照均匀分布或高斯分布
  • Xavier方法（2010）：前传时维持激活值的方差，反传维持梯度的方差
  • Kaiming方法（2015）：同上，但针对ReLU激活函数
• 用训练好的模型进行初始化：
  • 替换预训练模型的分类头，进行微调训练（finetune）

1.7 防止过拟合的策略

• 
  早停（Early Stopping）
  
  ：将训练数据集划分为训练集和验证机，在训练集上训练，周期性在验证集上测试。当验证集的loss不降反升时，停止训练，防止过拟合。
• 
  正则化与权重衰减
  
  ：（奥卡姆剃刀原理：我们认为世界是简单的，当有两个模型都能拟合我们的数据时，我们倾向于选择简单的模型）
  • 在损失函数中引入正则化项，这个正则项用来惩罚模型的复杂度（经验风险），以鼓励训练出相对简单的模型。
  • 最终去优化结构风险：结构风险 = 损失函数 + 经验风险（正则项）
  • 注意梯度更新策略中，经验风险合并到权重初值上去了，只不过是乘了个常数系数，变成了权重衰减项。这就使得我们的梯度下降算法优化策略变成了两个步骤
    • 首先在某个位置，把
      
      参数缩小
      
      一点，然后再按照算出来的梯度方向
      
      往前走一步
      

1.8 数据增广策略

• 泛化性好的模型需要大量多样化的数据，而数据的采集标注是有成本的
• 可以利用简单的随机变换，从一张图片扩充出多张图片

1.9 Batch Normalization

• 在一个Batch中，对神经元响应进行归一化，使每层的输出有相对稳定的数值分布。从而降低网络的学习难度，提高训练的稳定性，并允许使用更大的学习率
• 但是呢，强行的归一化到0均值1方差的分布，可能会是数据多样性一定程度的被破坏，因此我们会加上一个γ和β对它进行一个扩展
• 在归一化之后进行仿射变换扩大数值范围，方向和幅度的分解
• 推理时没有batch，使用统计量的平均值
• BN一般用于卷积层，将同意通道内，不同空间位置，来自不同样本的所有响应值归为一组进行归一化
• 应用BN的卷积层一般不需要bias
• 其他的Normalization

1.10 总结

• 随机梯度下降为主，各种经验策略辅助
• 损失函数高度不规则，非凸
  • 权重初始化：kaiming init，预训练模型
  • 优化器改进：动量SGD，自适应梯度算法
  • 学习率策略：学习率退火，升温
• 防止过拟合
  • 数据增广、早停、Dropout
• Batch Normalization：稳定数据分布，降低训练难度

2. PyTorch框架简介

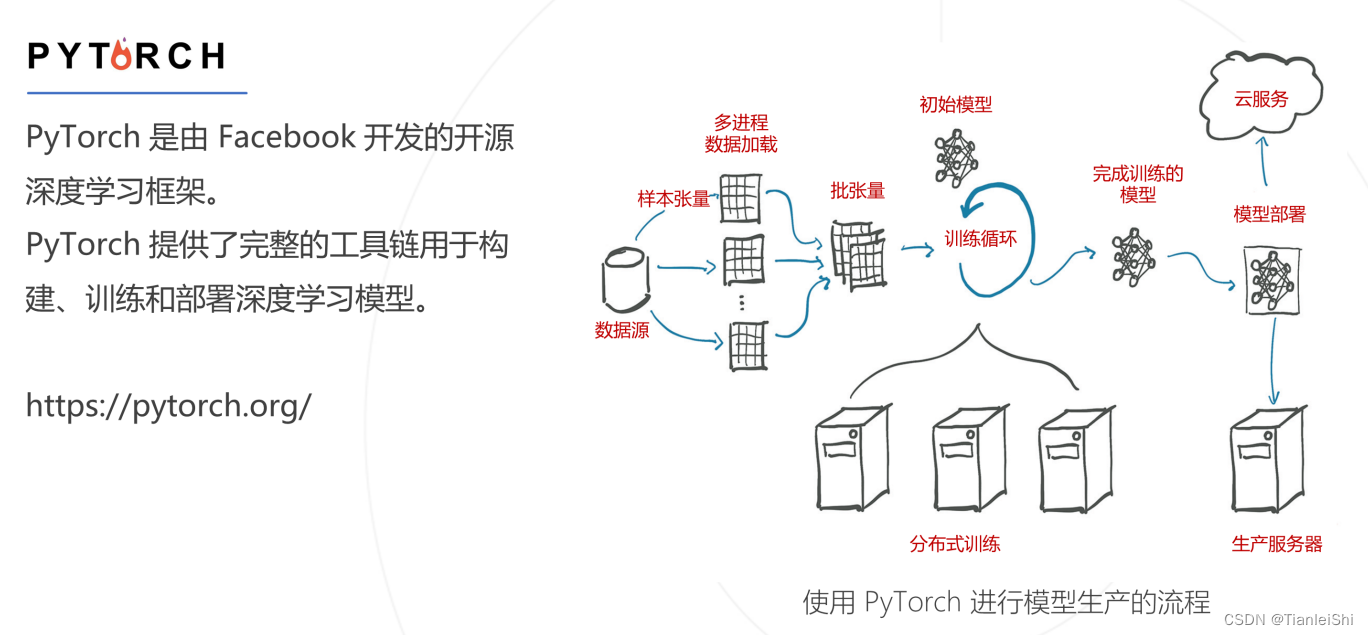
2.1 PyTorch的基本模块

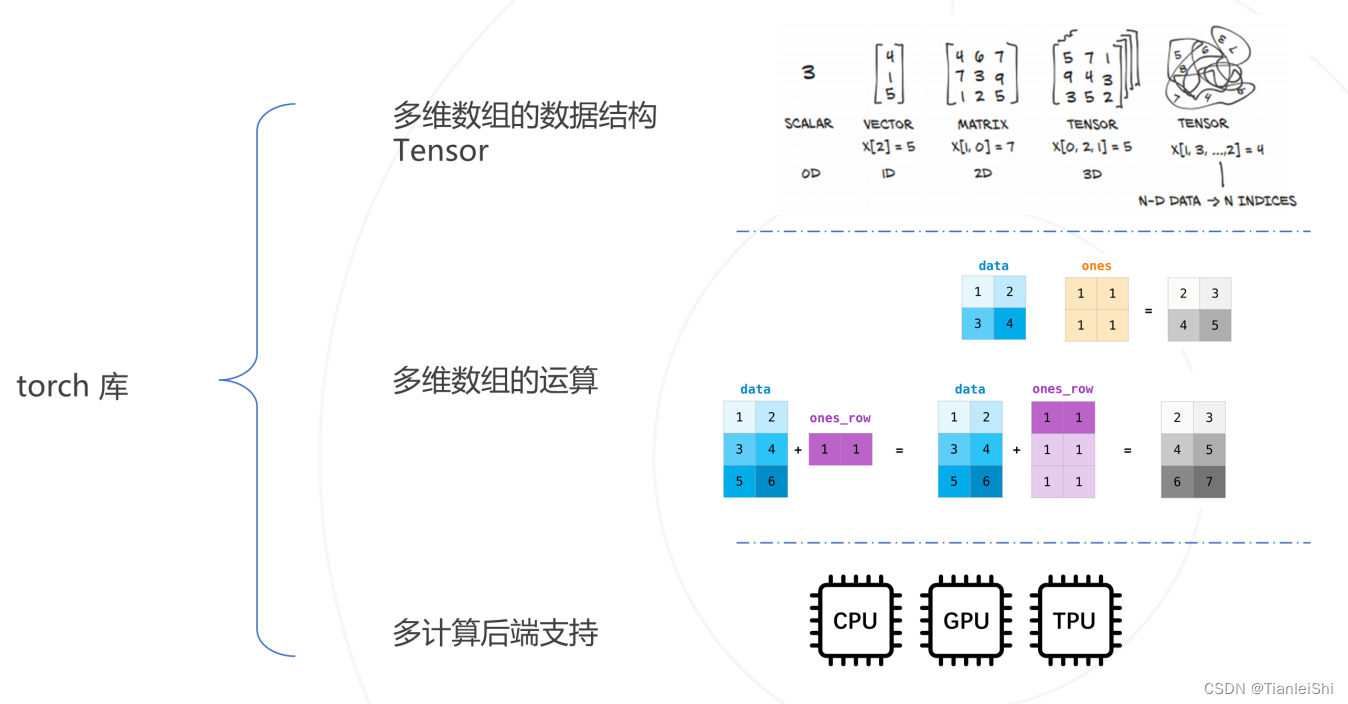
2.2 数值计算库torch

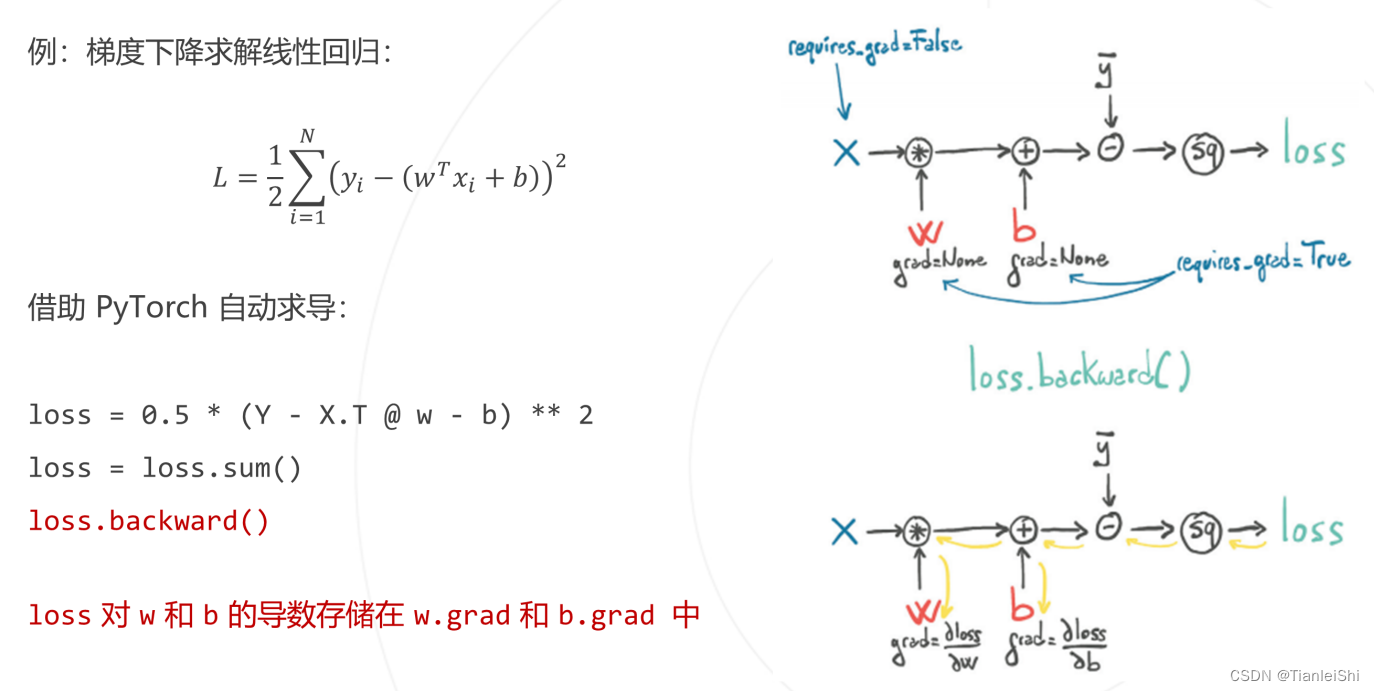
2.3 自动求导torch.autograd

2.4 函数库torch.nn.functional

• 提供了构建神经网络所需的计算函数：线性函数、卷积、池化、非线性激活、归一化等

import torch
import torch.nn.functional as F
# ReLU non-linear activation
x = torch.randn(3,3)
y = F.relu(x)

# Max Pooling
x = torch.randn(1,1,4,4)
y = F.max_pool2d(x,kernel_size=2,stride=2)

# Convolution
img = torch.randn(1,3,8,12)
weight = torch.randn(6,3,3,3)
bias = torch.randn(6)
out = F.conv2d(img,weight,bias,padding=1)

2.5 通用模型封装torch.nn.Module

2.6 优化器torch.optim

2.7 数据工具torch.utils.data