第
1
小题
二叉排序树的操作,实现如下6个功能:
(
1
)设计思路
要求建立一棵二叉排序树:对从键盘输入的顺序任意的若干个正整数建立一颗二叉排序树,以-1作为结束。
例如:输入 39 11 68 46 75 23 71 8 86 34 -1
插入一个数据,首先使用find函数判断这个数据是不是已经存在了,已经存在的数据不能再插入。同时,find函数会返回被查结点的双亲f,如果没查找到,则f就是待插入的结点的双亲。
若这个数据未存在,判断要插入的位置。
先判断是否是空树,如果是空树,则插入到根结点,否则判断是待插入位置的结点的左孩子还是右孩子
-
源代码


(
3
)说明
(请说明上述源代码是否应用测试程序进行测试并得到正确结果,如果存在错误,请描述错误并适当分析错误可能发生的原因)
已经用测试程序进行测试,并得到正确结果。
第
2
小题
-
设计思路
要求中序遍历,输出遍历结果。
(阐述通过分析问题得到解决方案的思考过程)
使用之前实验的中序遍历的算法就好了
(
2
)源代码
(请在源代码中添加注释,对变量含义、代码含义进行适当说明)

(
3
)说明
(请说明上述源代码是否应用测试程序进行测试并得到正确结果,如果存在错误,请描述错误并适当分析错误可能发生的原因)
已经用测试程序进行测试,并得到正确结果。
第
3
小题
(
1
)设计思路
(阐述通过分析问题得到解决方案的思考过程)
要求输入一个关键字,进行查找。
参数列表为数据元素,所以重载一个参数列表为数据元素类型的find函数。
从根结点开始比较,如果等于key则查找成功,用一个标志存储temp查找结果,查找到了temp就等于1.
如果key大于根结点的值,则到左子树中查找,小于则到右子树时查找,当p为空或查到找key时,查找结束
(
2
)源代码
(请在源代码中添加注释,对变量含义、代码含义进行适当说明)
(
3
)说明
(请说明上述源代码是否应用测试程序进行测试并得到正确结果,如果存在错误,请描述错误并适当分析错误可能发生的原因)
已经用测试程序进行测试,并得到正确结果。
第
4
小题
(
1
)设计思路
(阐述通过分析问题得到解决方案的思考过程)
要求输入一个关键字,进行插入。
同(1),使用插入函数就好
(
2
)源代码
(请在源代码中添加注释,对变量含义、代码含义进行适当说明)
(
3
)说明
(请说明上述源代码是否应用测试程序进行测试并得到正确结果,如果存在错误,请描述错误并适当分析错误可能发生的原因)
已经用测试程序进行测试,并得到正确结果。
第
5
小题
(
1
)设计思路
删除:输入一个关键字,进行删除。
要删除二叉排序树中的p结点,分三种情况:
- p为叶子结点,只需修改p双亲f的指针f->leftchild=NULL或f->rightchild=NULL;
- p只有左子树或右子树
p只有左子树,用p的左孩子代替p
p只有右子树,用p的右孩子代替p
- p左、右子树均非空,
在p的左子树中寻找关键字值最大的数据元素(中序遍历中最后一个被访问的数据元素) x,用x的值代替被删除数据元素的值,再来删除数据元素x(x没有右子树);
据此,设计出参数列表为BinTreeNode *类型的Delete函数。题目要求所删元素类型为数据元素类型,所以还需要再重载一个参数列表为ElemType类型的函数。
重载后,使用find(key,*f)函数,利用f得到待删结点的双亲结点,再判断待删结点是双亲结点的左孩子还是右孩子。
若待删结点无双亲,则待删结点为根结点,则需要删除根结点。
(
2
)源代码
(
3
)说明
(请说明上述源代码是否应用测试程序进行测试并得到正确结果,如果存在错误,请描述错误并适当分析错误可能发生的原因)
已经用测试程序进行测试,并得到正确结果。
第
6
小题
(
1
)设计思路
(阐述通过分析问题得到解决方案的思考过程)
要求编写递归算法,从大到小输出关键字不小于x的数据元素。
定义一个PrintNLT(BinarySortTree<int> &tree, BinTreeNode<int> *p, int boundary)函数,作用是输出以p为根结点的树中,比boundary值大的元素。
由于需要从大到小输出,所以
若p有右孩子,则以p的右孩子为根调用PrintNLT函数,这样就可以输出p的右子树中比boundary大的元素
再判断p的元素是否大于等于boundary,符合则输出
若p有左子树,最后再递归地调用PrintNLT输出左子树中比boundary大的元素就好了
(
2
)源代码
(请在源代码中添加注释,对变量含义、代码含义进行适当说明)

(
3
)说明
(请说明上述源代码是否应用测试程序进行测试并得到正确结果,如果存在错误,请描述错误并适当分析错误可能发生的原因)
已经用测试程序进行测试,并得到正确结果。
源代码:

#include <iostream>
using namespace std;
#include "status.h"
#include "Node.h"
#include "LinkQueue.h"
#include "BinTreeNode.h"
#include "BinarySortTree.h"
BinTreeNode<int> *FindBoundary(BinTreeNode<int> *p, int boundary);
template <class Elemtype>
void Display(const Elemtype e)
{
cout << e << " ";
}
void PrintNLT(BinarySortTree<int> &tree, BinTreeNode<int> *p, int boundary) //输出以p为根的子树中大于boundary的结点
{
//先从p的左右子树中输出
if (p->rightChild)
{
PrintNLT(tree, p->rightChild, boundary);
}
// 右子树比较完,比较p
if (p->data >= boundary)
cout << p->data << " ";
// p比较完,比较p的左子树
if (p->leftChild)
PrintNLT(tree, p->leftChild, boundary);
}
BinTreeNode<int> *FindBoundary(BinTreeNode<int> *p, int boundary) //在以p结点为根的子树中寻找临界结点
{
//中序寻找temp结点,temp->leftChild < boundary <= temp
if (boundary <= p->data) // p结点的值不小于boundary时,从左子树中寻找临界结点,不存在返回p
{
//左子树为空:这个结点就是所要寻找的临界结点
if (p->leftChild == NULL)
{
cout << p->data << "shuaige1" << endl;
return p;
}
//左子树不为空:在它的左子树中寻找临界结点
else
{
//如果左子树中有临界结点
BinTreeNode<int> *temp = FindBoundary(p->leftChild, boundary);
if (temp)
{
cout << p->data << "shuaige2" << endl;
return temp;
}
//如果没有,返回p
else
{
cout << p->data << "shuaige3" << endl;
return p;
}
}
}
else // p->data 小于 boundary时,从右子树中寻找boundary,不存在说明没有结点比boundary大,返回NULL
{
//右子树不存在,说明这个子树中没有结点比boundary大
if (p->rightChild == NULL)
return NULL;
//右子树不为空,从右子树中寻找boundary,如果能找到boundary,return,都比boundary小,return NULL
else
{
//右子树大于等于boundary,则右子树就是临界结点
BinTreeNode<int> *temp = FindBoundary(p->rightChild, boundary);
if (temp)
{
cout << p->data << "shuaige3" << endl;
return temp;
}
//如果没有,返回p
else
return NULL;
}
}
}
int main(void)
{
BinarySortTree<int> tree;
int data;
//建立二叉排序树
cout << "Please enter 10 integers, ending with -1(39 11 68 46 75 23 71 8 86 34 -1):" << endl; //输入:39 11 68 46 75 23 71 8 86 34 -1
cin >> data;
while (data != -1)
{
tree.Insert(data); //-----------二叉排序树插入
cin >> data;
}
//中序遍历二叉排序树
cout << "The inorder sequence of the binary sorting tree is:" << endl;
tree.InOrder(Display); //-----------二叉排序树中序遍历
cout << endl;
//查找
cout << "Please enter the data to be searched(39):" << endl;
cin >> data; //输入:39
if (tree.Find(data)) //-----------二叉排序树查找
cout << "Search Successfully!" << endl;
else
cout << "Not Found!" << endl;
//插入
cout << "Please enter the data to be inserted(55):" << endl;
cin >> data; //输入:55
if (tree.Insert(data)) //-----------二叉排序树插入
cout << "Insert successfully!" << endl;
else
cout << "Insert unsuccessfully!" << endl;
cout << "The inorder sequence of the binary sorting tree is:" << endl;
tree.InOrder(Display);
cout << endl;
//删除
cout << "Please enter the data to be deleted(71):" << endl;
cin >> data; //输入:71
if (tree.Delete(data)) //-----------二叉排序树删除
{
cout << "Delete successfully!" << endl;
}
else
cout << "Delete unsuccessfully!" << endl;
cout << "The inorder sequence of the binary sorting tree is:" << endl;
tree.InOrder(Display);
cout << endl;
//从大到小输出关键字不小于x的数据元素
cout << "Please enter a data as a boundary(34):" << endl;
cin >> data; //输入:34
cout << "Data greater than the boundary " << data << " include:" << endl;
PrintNLT(tree, tree.GetRoot(), data); //-----------降序输出不小于data的所有元素
cout << endl;
system("pause");
return 0;
}#pragma once
#include "BinTreeNode.h"
template <class ElemType>
class BinarySortTree
{
protected:
BinTreeNode<ElemType> *root;
void Destroy(BinTreeNode<ElemType> *&r); //删除以r为根的二叉树
void PreOrder(BinTreeNode<ElemType> *r, void (*Visit)(const ElemType &)) const; //先序遍历以r为根的二叉树
//中序遍历以r为根的二叉树
void PostOrder(BinTreeNode<ElemType> *r, void (*Visit)(const ElemType &)) const; //后序遍历以r为根的二叉树
int Height(const BinTreeNode<ElemType> *r) const; //求以r为根的二叉树的高度
int NodeCount(const BinTreeNode<ElemType> *r) const; //求以r为根的二叉树的结点个数 //在以r为根的二叉树中求p的双亲
BinTreeNode<ElemType> *Parent(BinTreeNode<ElemType> *r, const BinTreeNode<ElemType> *p) const; //在以r为根的二叉树中求p的双亲
public:
void InOrder(BinTreeNode<ElemType> *r, void (*Visit)(const ElemType &)) const;
bool Delete(const ElemType e);
void Delete(BinTreeNode<ElemType> *&p);
BinTreeNode<ElemType> *Find(const ElemType &key, BinTreeNode<ElemType> *&f) const;
bool Find(const ElemType &key) const;
bool Insert(const ElemType &e);
BinarySortTree();
BinarySortTree(const ElemType &e);
~BinarySortTree();
BinTreeNode<ElemType> *GetRoot() const;
bool IsEmpty() const;
Status GetElem(BinTreeNode<ElemType> *p, ElemType &e) const;
Status SetElem(BinTreeNode<ElemType> *p, const ElemType &e);
void InOrder(void (*Visit)(const ElemType &)) const; //中序遍历整棵二叉树
void PreOrder(void (*Visit)(const ElemType &)) const; //先序遍历整棵二叉树
void PostOrder(void (*Visit)(const ElemType &)) const; //后序遍历整棵二叉树
void LevelOrder(void (*Visit)(const ElemType &)) const; //层序遍历整棵二叉树
int NodeCount() const;
void CreateBinaryTree();
int Depth() const;
int depth(BinTreeNode<ElemType> *rt) const;
int CountLeaf(BinTreeNode<ElemType> *rt) const;
int Width() const;
int width(LinkQueue<BinTreeNode<ElemType> *> &q, int &maxWidth, int wid) const;
int CtLeaf(LinkQueue<BinTreeNode<ElemType> *> &q, int &count) const;
// void PrintNLT(BinarySortTree tree,BinTreeNode<ElemType> *root,ElemType boundary) const;
};
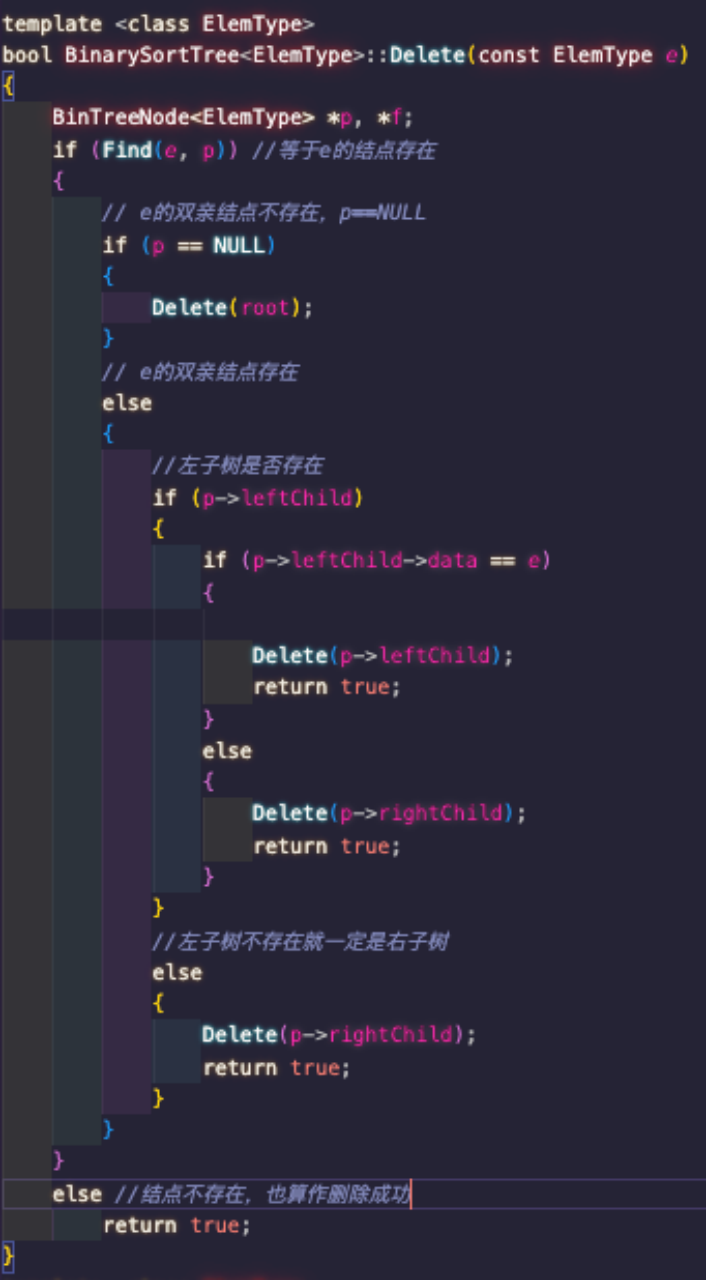
template <class ElemType>
bool BinarySortTree<ElemType>::Delete(const ElemType e)
{
BinTreeNode<ElemType> *p, *f;
if (Find(e, p)) //等于e的结点存在
{
// e的双亲结点不存在,p==NULL
if (p == NULL)
{
Delete(root);
}
// e的双亲结点存在
else
{
//左子树是否存在
if (p->leftChild)
{
if (p->leftChild->data == e)
{
Delete(p->leftChild);
return true;
}
else
{
Delete(p->rightChild);
return true;
}
}
//左子树不存在就一定是右子树
else
{
Delete(p->rightChild);
return true;
}
}
}
else //结点不存在,也算作删除成功
return true;
}
template <class ElemType>
void BinarySortTree<ElemType>::Delete(BinTreeNode<ElemType> *&p)
{
BinTreeNode<ElemType> *tmpPtr, *tmpF;
if (p->leftChild == NULL && p->rightChild == NULL) // p为叶子结点
{
delete p;
p = NULL;
}
else if (p->leftChild == NULL) // p的左子树为空,右孩子代替自己
{
tmpPtr = p;
p = p->rightChild;
delete tmpPtr;
}
else if (p->rightChild == NULL) // p的右子树为空,左孩子代替自己
{
tmpPtr = p;
p = p->leftChild;
delete tmpPtr;
}
else
{ // p左右子树都在,采用前述方案一
tmpF = p;
tmpPtr = p->leftChild;
while (tmpPtr->rightChild != NULL) //寻找p的左子树中关键字最大的结点
{
tmpF = tmpPtr;
tmpPtr = tmpPtr->rightChild;
} // p代表双亲结点的孩子指针,修改p就是修改双亲结点的孩子指针!
p->data = tmpPtr->data; //将tmpPtr结点的数据值赋值给待删结点
//删除tmpPtr结点
if (tmpF->rightChild == tmpPtr)
Delete(tmpF->rightChild);
else //待删结点p左子树中只有一个结点,tmpF==p,tmpPtr==tmpF->leftChild
Delete(tmpF->leftChild);
}
}
template <class ElemType>
bool BinarySortTree<ElemType>::IsEmpty() const
{
if (root == NULL)
return true;
else
return false;
}
template <class ElemType>
bool BinarySortTree<ElemType>::Insert(const ElemType &e)
{
BinTreeNode<ElemType> *f; //指向被查找结点的双亲
if (Find(e, f) == NULL)
{ //待插元素不存在,进行插入
BinTreeNode<ElemType> *p;
p = new BinTreeNode<ElemType>(e); //新建一个结点
if (IsEmpty())
root = p; //空树
else if (e < f->data)
f->leftChild = p; //插入为左孩子
else
f->rightChild = p; //插入为右孩子
return true;
}
return false; //待插元素已存在,插入失败
}
template <class ElemType>
BinTreeNode<ElemType> *BinarySortTree<ElemType>::Find(const ElemType &key, BinTreeNode<ElemType> *&f) const
{
BinTreeNode<ElemType> *p = GetRoot(); //获取当前根结点
f = NULL; //指向p结点的双亲结点
while (p != NULL && p->data != key)
{
if (key < p->data)
{
f = p;
p = p->leftChild;
}
else
{
f = p;
p = p->rightChild;
}
}
return p;
}
template <class ElemType>
bool BinarySortTree<ElemType>::Find(const ElemType &key) const
{
BinTreeNode<ElemType> *p = GetRoot(); //获取当前根结点
int temp = 0;//是否查找到的标志
while (p != NULL)
{
if (p->data == key)//p等于key,表示查找到,程序结束
{
temp = 1;
break;
}
if (key < p->data)//比key大则在左子树中查找
{
p = p->leftChild;
}
else//比key小则在右子树中查找
{
p = p->rightChild;
}
}
if (temp == 0)
return false;
if (temp == 1)
return true;
}
template <class ElemType>
int BinarySortTree<ElemType>::CtLeaf(LinkQueue<BinTreeNode<ElemType> *> &q, int &count) const
{
BinTreeNode<ElemType> *t;
q.DelQueue(t);
if (t->leftChild == NULL && t->rightChild == NULL)
count++; //如果没有左右子树,则为叶子
//有左右子树时,将左右子树加入到队列中去
if (t->leftChild != NULL)
q.EnQueue(t->leftChild);
if (t->rightChild != NULL)
q.EnQueue(t->rightChild);
if (q.IsEmpty()) //当队列为空时,递归结束
return count;
else
CtLeaf(q, count);
}
template <class ElemType>
int BinarySortTree<ElemType>::CountLeaf(BinTreeNode<ElemType> *rt) const
{
LinkQueue<BinTreeNode<ElemType> *> q;
int count = 0;
if (root != NULL)
q.EnQueue(root);
CtLeaf(q, count);
// int count = 0;
// //层序遍历二叉树,若一个结点没有左右子树,则为叶子
// LinkQueue<BinTreeNode<ElemType> *> q;
// BinTreeNode<ElemType> *t;
// if (root != NULL)
// q.EnQueue(root);
// while (!q.IsEmpty())
// {
// q.DelQueue(t);
// if (t->leftChild == NULL && t->rightChild == NULL)
// count++; //如果没有左右子树,则为叶子
// if (t->leftChild != NULL)
// q.EnQueue(t->leftChild);
// if (t->rightChild != NULL)
// q.EnQueue(t->rightChild);
// }
return count;
}
template <class ElemType>
int BinarySortTree<ElemType>::width(LinkQueue<BinTreeNode<ElemType> *> &q, int &maxWidth, int wid) const
{
//根据上一层的结点,可以计算出这层的结点个数,结点放在队列中,q队列中保存上一层的结点
// wid为上一层的结点数目
BinTreeNode<ElemType> *t;
int num = 0; //记录本层结点数
for (int i = 0; i < wid; i++)
{
q.DelQueue(t);
if (t->leftChild != NULL)
{
num++;
q.EnQueue(t->leftChild);
}
if (t->rightChild != NULL)
{
num++;
q.EnQueue(t->rightChild);
}
}
if (num > maxWidth)
maxWidth = num;
if (q.IsEmpty()) //递归结束条件为队列为空
{
return maxWidth;
}
width(q, maxWidth, num); //递归作用为循环
}
template <class ElemType>
int BinarySortTree<ElemType>::Width() const
{
LinkQueue<BinTreeNode<ElemType> *> q;
int maxWidth = 1;
if (root != NULL)
q.EnQueue(root);
width(q, maxWidth, maxWidth);
return maxWidth;
}
// template <class ElemType>
// int BinarySortTree<ElemType>::Width() const
// {
// //每遍历一层,返回本层的宽度
// LinkQueue<BinTreeNode<ElemType> *> q;
// int width = 0, n = 0, m;//width为最大宽度,n记录上一层的结点数,m为本层结点数
// BinTreeNode<ElemType> *t;
// if (root != NULL)
// {
// q.EnQueue(root);
// width = 1;
// n = 1;
// }
// while (!q.IsEmpty())//队列为空时结束循环
// {
// m = 0;//记录本层结点数
// for (int i = 0; i < n; i++)//将上一层n个结点依次出队
// {
// q.DelQueue(t);
// if (t->leftChild != NULL)
// {
// m++;
// q.EnQueue(t->leftChild);
// }
// if (t->rightChild != NULL)
// {
// m++;
// q.EnQueue(t->rightChild);
// }
// }
// n = m;//上一层结点已经全部出队,n记录结点数
// if (n > width)
// width = n;
// }
// return width;
// }
template <typename ElemType>
int BinarySortTree<ElemType>::depth(BinTreeNode<ElemType> *rt) const
{
//二叉树的深度等于左右子树深度中较大值+1,为空树时深度为0
int wid = 0;
if (rt == NULL)
return wid;
else
{
if ((width(rt->leftChild) > width(rt->rightChild)))
wid = width(rt->leftChild) + 1;
else
wid = width(rt->rightChild) + 1;
return wid;
}
}
template <typename ElemType>
int BinarySortTree<ElemType>::Depth() const
{
return depth(root);
}
template <typename ElemType>
BinTreeNode<ElemType> *BinarySortTree<ElemType>::GetRoot() const
{
return root;
}
template <class ElemType>
void BinarySortTree<ElemType>::PreOrder(BinTreeNode<ElemType> *r, void (*Visit)(const ElemType &)) const
{
if (r != NULL)
{
(*Visit)(r->data); //首先访问根节点
PreOrder(r->leftChild, Visit); //再遍历r的左子树
PreOrder(r->rightChild, Visit); //最后遍历r的右子树
}
}
template <class ElemType>
void BinarySortTree<ElemType>::PreOrder(void (*Visit)(const ElemType &)) const { PreOrder(root, Visit); }
template <class ElemType>
BinarySortTree<ElemType>::~BinarySortTree() { delete root; }
template <class ElemType>
BinarySortTree<ElemType>::BinarySortTree(const ElemType &e)
{
root->data = e.data;
}
template <class ElemType>
BinarySortTree<ElemType>::BinarySortTree()
{
root = NULL;
}
template <class ElemType>
void BinarySortTree<ElemType>::PostOrder(BinTreeNode<ElemType> *r, void (*Visit)(const ElemType &)) const
{
if (r != NULL)
{
PostOrder(r->leftChild, Visit); //首先遍历r的左子树
PostOrder(r->rightChild, Visit); //再遍历r的右子树
(*Visit)(r->data); // 最后访问根结点r
}
}
template <class ElemType>
void BinarySortTree<ElemType>::PostOrder(void (*Visit)(const ElemType &)) const { PostOrder(root, Visit); }
template <class ElemType>
void BinarySortTree<ElemType>::LevelOrder(void (*Visit)(const ElemType &)) const
{
LinkQueue<BinTreeNode<ElemType> *> q;
BinTreeNode<ElemType> *t;
if (root != NULL)
q.EnQueue(root);
while (!q.IsEmpty())
{
q.DelQueue(t);
(*Visit)(t->data);
if (t->leftChild != NULL)
q.EnQueue(t->leftChild);
if (t->rightChild != NULL)
q.EnQueue(t->rightChild);
}
}
template <class ElemType>
void BinarySortTree<ElemType>::InOrder(BinTreeNode<ElemType> *r, void (*Visit)(const ElemType &)) const
{
if (r != NULL)
{
InOrder(r->leftChild, Visit); //首先遍历r的左子树
(*Visit)(r->data); //再访问根节点r
InOrder(r->rightChild, Visit); //最后遍历r的右子树
}
}
template <class ElemType>
void BinarySortTree<ElemType>::InOrder(void (*Visit)(const ElemType &)) const
{
InOrder(root, Visit);
}
template <class ElemType>
void BinarySortTree<ElemType>::CreateBinaryTree()
{
CreateBtr(root);
}
void CreateBtr(BinTreeNode<char> *&r)
{
char ch;
cin >> ch;
if (ch == '#')
r = NULL;
else
{
r = new BinTreeNode<char>(ch); //先序序列,就先给根创建
CreateBtr(r->leftChild); // r的左孩子看成根递地归创建
CreateBtr(r->rightChild); // r的右孩子看成根递归地创建
}
}
#pragma once
template <class ElemType>
struct BinTreeNode{
ElemType data; // 数据域
BinTreeNode<ElemType> *leftChild; // 左孩子指针域
BinTreeNode<ElemType> *rightChild; // 右孩子指针域
BinTreeNode(); // 无参数的构造函数
BinTreeNode(const ElemType &d, BinTreeNode<ElemType> *lChild = NULL, BinTreeNode<ElemType> *rChild = NULL);
};
template <class ElemType>
BinTreeNode<ElemType>::BinTreeNode()
{
leftChild = rightChild = NULL;
}
template <class ElemType>
BinTreeNode<ElemType>::BinTreeNode(const ElemType &d, BinTreeNode<ElemType> *lChild, BinTreeNode<ElemType> *rChild)
{
data = d;
leftChild = lChild;
rightChild = rChild;
}#pragma once
#include "Node.h"
template<class ElemType> class LinkQueue {
protected:
Node<ElemType> *front, *rear; // 队头队尾指针
public:
LinkQueue();
virtual ~LinkQueue();
int GetLength() const;
bool IsEmpty() const;
void Clear();
Status DelQueue(ElemType &e);
Status GetHead(ElemType &e) const;
Status EnQueue(const ElemType e);
void Traverse(void (*Visit)(const ElemType &)) const;
};
template<class ElemType>
Status LinkQueue<ElemType>::DelQueue(ElemType &e){
if (!IsEmpty()) { Node<ElemType> *p = front->next;
e = p->data;
front->next = p->next;
if (rear == p) rear = front;//队列中只有一个元素
delete p;
return SUCCESS; }
else
return OVER_FLOW;
}
template<class ElemType>
Status LinkQueue<ElemType>::EnQueue(const ElemType e) {
Node<ElemType> *p;
p = new Node<ElemType>(e);
if (p) {
rear->next = p;
rear = rear->next;
return SUCCESS;
}
else
return OVER_FLOW;
}
template<class ElemType>
Status LinkQueue<ElemType>::GetHead(ElemType &e) const {
if (!IsEmpty()) {
e = front->next->data;
return SUCCESS;
}
else
return OVER_FLOW;
}
template<class ElemType>
void LinkQueue<ElemType>::Clear() {
Node<ElemType> *p = front->next;
while (p != NULL) {
front->next = p->next;
delete p;
p = front->next;
}
rear = front;
}
template<class ElemType> LinkQueue<ElemType>::~LinkQueue() {
Clear();
delete front;
}
//判断链式队列是否为空
template<class ElemType>
bool LinkQueue<ElemType>::IsEmpty() const {
return rear == front;
}
template<class ElemType> LinkQueue<ElemType>::LinkQueue()
{
rear = front = new Node<ElemType>();
}
#pragma once
template<class ElemType>
struct Node{
ElemType data;
Node<ElemType>* next;
Node();
Node(ElemType e,Node<ElemType>* link = NULL);
};
template<class ElemType>
Node<ElemType>::Node()
{
next = NULL;
data = 0;
}
template<class ElemType>
Node<ElemType>::Node(ElemType e,Node<ElemType> *link)
{
data = e;
next = link;
}
#pragma once
typedef enum{NOT_PRESENT,ENTRY_FOUND,RANGE_ERROR,SUCCESS,OVER_FLOW} Status ;