深入浅出理解FFT算法,通俗易懂,用xilinxIP核心仿真
1、前言:傅里叶变换:时域到频域的转换
FS连续时间周期傅里叶级数->DFS离散傅里叶级数->FT连续时间非周期信号的傅里叶变换->
DTFT离散时间傅里叶变换->DFT离散时域傅里叶变换->DFT离散频域傅里叶变换->FFT快速傅里叶变换
其中,
FS、DFS、FT都是连续信号,必须经过采样计算机才能处理
DTFT是对时间域采样,时域离散化则频域连续,对于连续的频域计算机是不能处理的
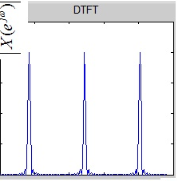
DTFT时域采样所以频率连续
DFT 是对频率域采样,频域离散化时域连续,离散的频域分量构成频谱图,计算机可以处理,DFT将离散的时间序列转化为离散的频率序列
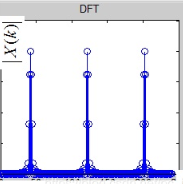
FFT DFT的快速算法,FFT实际上就是DFT的子集,本质就是一种分治算法,利用DFT的特性,通过分治算法不断的2分、4分或者不规则分法(分裂基)极大的降低了计算量
FFT的最基础应用,频谱仪、示波器频率幅度测量—通过分析生成的频谱得到信号的频率和幅值
2、DFT与FFT原理与本质:
(1)DFT公式:
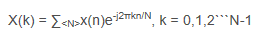
XK是频域序列,Xn是时域序列,由于e^-j2PIkn/N需要用欧拉公式展开成cosx+jsinx所以DFT是复数运算,避免不了做复数加(减)法与乘法
DFT计算量:假设现在有1024个点(n=0…1023)构成了时间序列XN,根据DFT公式,每得到一个频点XK需要1024个Xn每个去做一个复数乘法;但是还有1024个XK,这里光复数乘法的运算量就是1024
1024=1048576次,就是N^2次,每个复数乘法在计算机还内部不是一步到位的;计算机最小时钟单位时钟周期CLK,以4GHZ主频(clk)的计算机为例,一个时钟周期250PS,一次复数乘法估算10个时钟周期,那么一次复数乘法需要2.5ns,那么复数乘法计算需要2.62ms
但是还有复数加法,得到1个XK频点需要1024个值做加法,一共1023次;得到1024个频点需要1023
1024次复数加法,假设复数加法2个时钟周期,做完复数加法需要0.26ms
至此,我们用4GHZ的计算机把1024点的FFT计算完花费了约2.88ms;但是没完,计算出来的是复数,得到频点需要取模(根号下实部
2+虚部
2),然后再分析频谱得到频率,假设这里花费5ms,但是这只是低点数的DFT并且是一维的,由于是近似N^2的复数加法和复数乘法,为了点数稍微增大而提高频率、幅度测量精度,计算量会突增;而且,当DFT用于二维计算(图像矩阵)的时候计算量就是几何增长,你能忍受i9-10系的电脑处理个图像要十几秒甚至一分钟么,所以DFT要应用必须实现快速化,这就是FFT
(2)FFT
本质:分治算法
方法:基2-2分法 基本4-4分法 分裂基-奇数序列2分、偶数序列4分法
实现:利用Wn性质,逐级分治计算
FFT与DFT的根本问题就是围绕为什么能计算快速化?
这是FFT的根本意义
(i)FFT数学规律-WN对称性( 看(i)方便理解 )
因为e^-j2PIkn/N,他能展开成cosx+jsinx的形式
给你看一组数据,是我用C语言写的FFT,其中下面窗口生成的是256点的e
-j2PIkn/N的cos部分,也就是e
-j2PIkn/N的实部
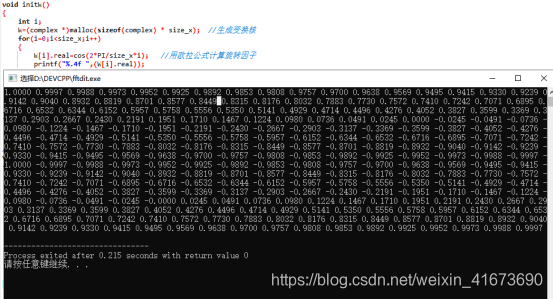
(要C代码留言就好)
观察这组数据就是按照cos变化规律来的,同理虚部jsinx按照sin规律变化
实际上cos+jsin就是一个圆,一个复平面上的园,笛卡尔的x轴就是cos,y轴就是sin
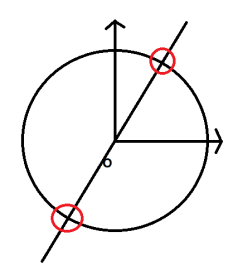
这个圆很显然具有对称性质,两个红圈就是cos+jsin和-(cos+jsin)
这就意味着e^-j2PIkn/N玩意算一半就好了,另一半取负就好了
假设某个Xk点的表达式Σxn(cos+jsin)形式,那么第1点和最中间那个点的cos+jsin不就是个公因式么?,提出来就是(x1-xn/2)(cos+jsin)的形式
得出结论相邻180度的点的值取负就好了
现在我们来认真切一下圆,找一下另外的关系
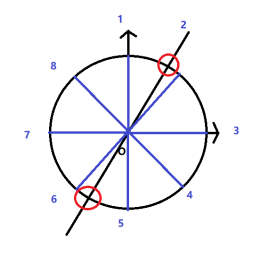
我们之前都是找的相邻180度的关系,可是
相邻90度
也有一个明显的关系,
根据DFT公式,我们以8点DFT为例子解析
e^-j2PIkn/N,当N=8时,n=0和n=2时分别计算,你展开后发现就是差±j,即90度
以上是对称性理解
而周期性很好理解,有个2PI怎么都消得掉
(ii)理解FFT蝶形
看完(i)后你能知道,DFT最重要的规律,即圆上点与点的规律
FFT是一种算法,你可以理解为切圆(排序)算法,只是他以一种特有的手段去切圆(排序)
在基2FFT内,这种手段就是分奇偶数切开,然后提出公因式来简化计算量;
对于基2算法而言,分出来的奇数序列和偶数序列分别计算,再重新编号分出个奇偶来继续算
重复以上步骤,直到每个小序列长度=2,剩下的这两个Xn再“内卷”
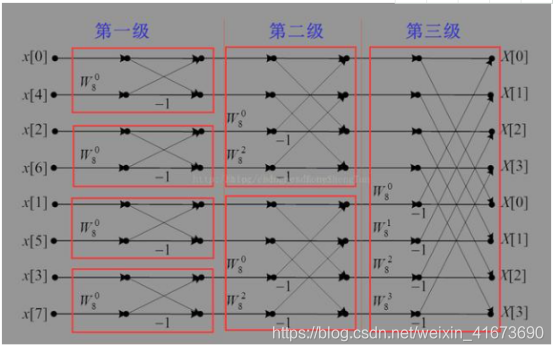
这是8点基2-DIT的蝶形图,
蝶形图解析
如下:
1、上面4个都是偶数,下面4个都是奇数且0-4,2-6是不是都相差180度?不就是个富豪的问题,这就是为了很好的提出公因式做了准备;
2、第一级算完又重新组合了,0-2,4-6一组,这时相邻差90度,不就是个±j的问题?而且0-2是上面4个序列的偶数排列,1-3是上面四个序列的奇数排列,2分就一直按照奇数偶数分下去
3、第二级又算完了,再分就只有2个xn了,再“内卷”就好了,2分了两次但是计算了三次,每次分都是按奇偶来的
如果还有疑惑,那么可以用数学公式理解一下,跟着箭头走向,我们算一遍:
首先,确定蝶形计算方式,
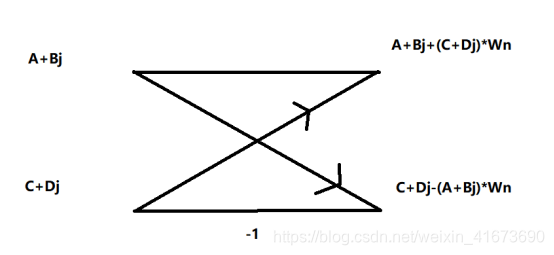
这个计算就是这样的,至于为什么这么算稍后会提到,先按照箭头走向,我们以生成的第二个频点X[1]为例计算
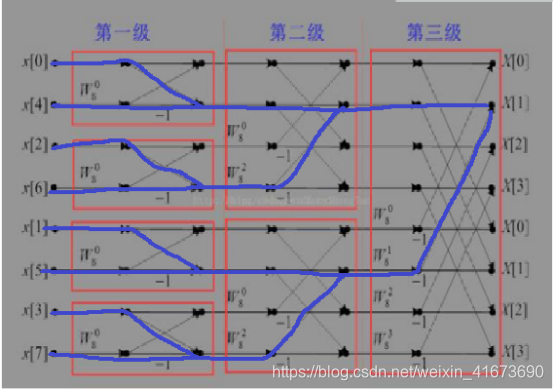
如图,你必须确认的是,对于X[1]而言,每个xn都参与了计算,而DFT的公式是:
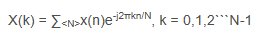
Wn=e^-j2PIkn/N
频点
X(1)=x(0)W8
0+x(1)W8
1+x(2)W8
2+x(3)W8
3+x(4)W8
4+x(5)W8
5+x(6)W8
6+x(7)W8
7
根据切圆的解释,我相信你能找到很多公因式,这里k=1的,如果k=2.3.4…n,有个2
PI项怎么都消了,所以只要对称性理解到位了,随便化简哈;
以上是DFT干的活,那蝶形图(FFT)是怎么算出X(1)的呢?
根据箭头流水线我们写出X(1)表达式:
X(1)=
( ( x(0)-x(4)W8^0 ) + ( x(2)-x(6)W8^0 )
W8^2) + ( ( x(1)-x(5)W8^0 ) + ( x(3)-x(7)W8^0 )
W8
2)*W8
1
你把它展开,和DFT的结果一毛一样
但是,这么写怎么能提高运算速度呢?
之前概述说过,影响DFT运算速度的只要是复数乘法,可以在FFT中,一个蝶形就少了一个复数乘法,因为
蝶形的Wn是共用的**,DFT没有这个排列,而是简单的从0加到N-1,所以可以戏称FFT你就是排了下序而已嘛,实际上它也是分治算法,每次奇数偶数分开,排列然后计算,没什么了不起的,只是一级降低一半计算量了对吧
第一次二分,提出公因式
第二次四分,提出公因式
第三次八分,提出公因式
一级减少一半,那么三级就降到8分之1了,是M级数
1/2的关系,有N个点,就是N
M/2个复数乘法
而复数加法,一个蝶形是两个复数加法,是复数乘法的两倍M
N,也远远低于N*(N-1)
(N比较大时)
(iii)理解把序列排回来(Rader算法-雷德算法-逆位序算法)
首先你看看基2FFT-DIT和DIF的8点蝶形
DIF

DIT
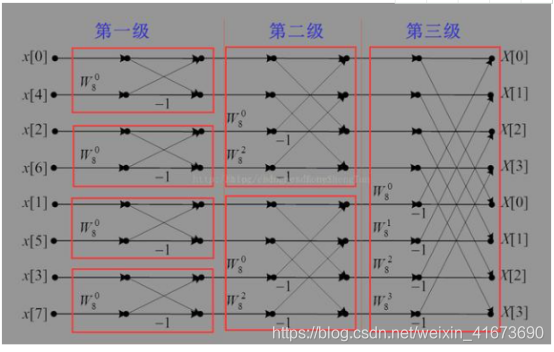
你有没有发现DIT输入乱序(按照奇数偶数排序),DIF输出乱序(按照奇数偶数排列),两个蝶形也长得很像压?其实没什么区别,所谓乱序就是按奇数偶数排了后继续分而已
但是这里有个逆序数规律
首先列出0-7二进制码 这边是逆序后的二进制码
000 000
001 100
010 010
011 110
100 001
101 101
110 011
111 111
左边是二进制数从左往右读,右边是二进制从右往左看,你会发现进制数是一样的,颇有计算机中大端模式小端模式的意思,通过这个规律,很容易的能转化成我们要的顺序排列数据
3.FFT在不同运算单元上的对比****(为什么要使用FPGA运算FFT?)**
(1)FFT在CPU/单片机上的运行
之前介绍过,我这有一份C语言的FFT运行代码,在计算机上运行,我们评估一下计算量

由于CPU核是一个周期一个周期的计算即串行运行,所以呀,FFT算法在CPU/单片机上运行是标准的
复数乘法:M
N
复数加法:M
N/2
(2)FFT在FPGA上的运行
FPGA是纯逻辑器件,可以并行运行
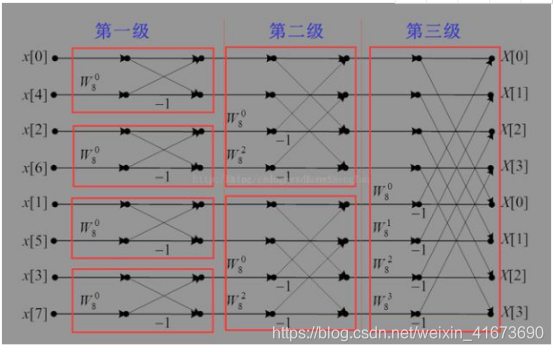
对于8点DIF的蝶形图,FPGA可以做到一个时钟周期将一级FFT算完,因为逻辑单元可以并行置入数据、计算,输出第一级结果;比如一个3输入数字电路与门,它可以ABC同时变化,对于单片机/CPU,只能先A B两个数运算,一个一个来,而FPGA最快可以一级一级来
对于FFT,一般最大级数不会超过20,意味这FPGA 20个时钟周期给你干完(这里就有点零延迟的味道了),单片机要几千甚至上万个周期,相同系统主频下,运算速度差异非常明显
(3)FPGA面积与速度的相互约束——流水线方式和普通的级联方式
FPGA内部逻辑单元不是无限的,例如你需要做4096点的基2FFT,如果要同时计算,那么每一级的每个蝶形需要一个复数乘法器和一个复数加法器,需要的资源是非常恐怖的,而且FPGA资源与芯片价格成正比,根据资源和功能的不同价格在几十到百万不等,需要的资源多价格就会非常贵;
如果你使用普通的级联方式,可以只用一个复数乘法器和一个复数加法器就解决问题,但是同样频率下这样速度和CPU有什么区别呢
这样就形成了一对矛盾,面积(资源)与速度的矛盾,想要快速,资源必然用的多,想要节省开支,必然影响速度
(流水线方式是所谓零延时的重要手段你自己补充,重在理解我不过多赘述)
4.XilinxISE环境下FFT IP核的介绍与使用(IP核自己扯一下)
IP核折衷了速度与面积,使用这可以在一定范围内可以选择速度和面积
这里对XilinxISE环境下的FFT IP核做简要介绍:
首先,FFT是复数输入复数输出,所以输入输出加起来至少4个,我们使用单通道即一次时钟周期置入一次数据
IP核生成的RTL图如下:
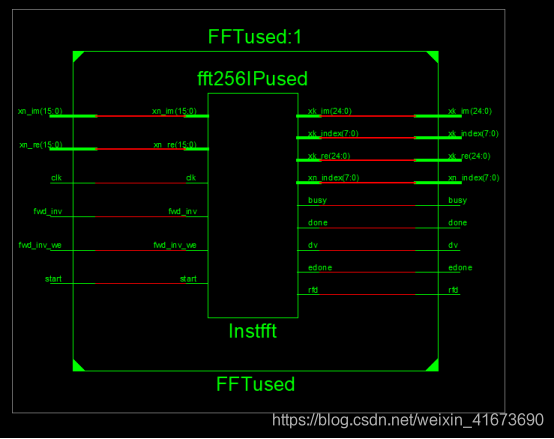
Xn是输入,分re实部核im虚部,clk是时钟,fwd和start相关是一些控制是能信号
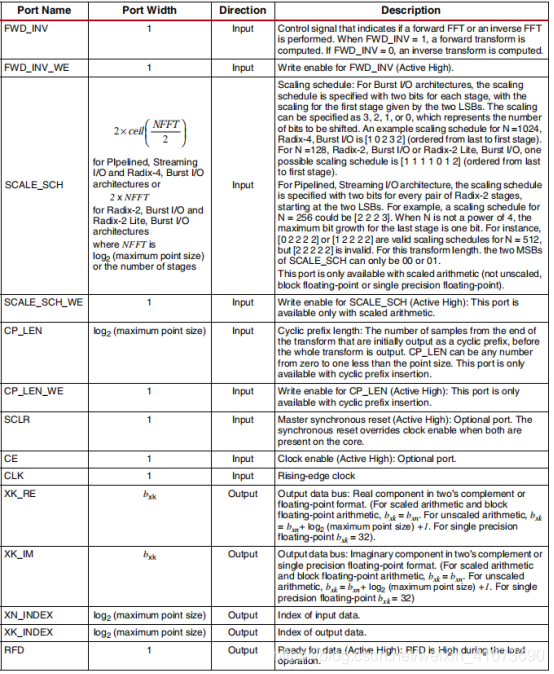
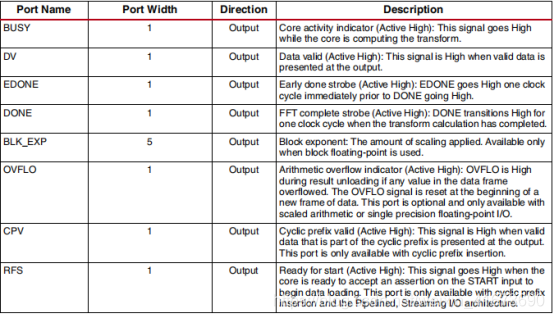
Xk是输出,也分re和im,只是输入输出位宽不一样,其余的是一些状态信号,具体内容见下表
IP核也可以配置,这里配置成256点,单通道StreamingIO(流水线方式—最快)
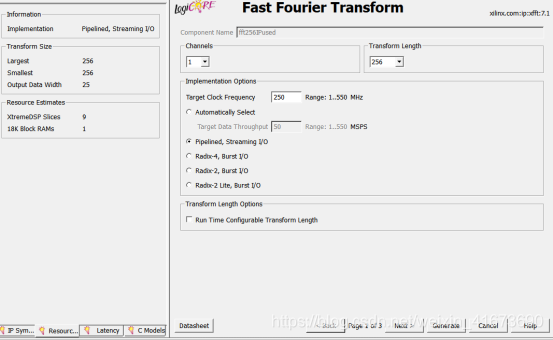
他需要600个周期算完
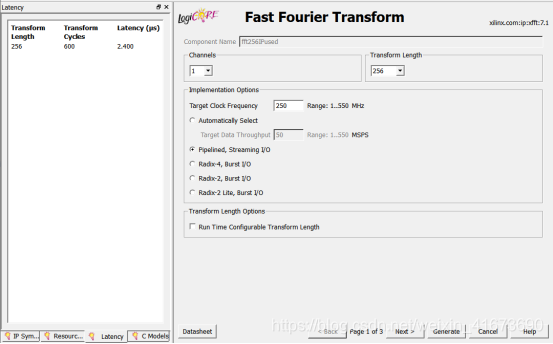
这与CPU相比,用的时钟周期是较低的了,基本上是最快的配置方式
配置好IP核后,进行verilog顶层例化然后综合仿真就可以了
5.XilinxISE IP核 FFT仿真波形图
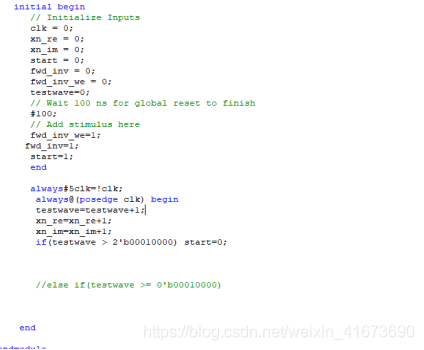
Test文件主代码,即在256点内构造一段斜坡让IP核去做变换,alway内是敏感信号表也是一个进程,增加到32关使能,等待结果就好了,在实际应用中,输入带虚部的较少,你自己可以去掉虚部
波形结果:
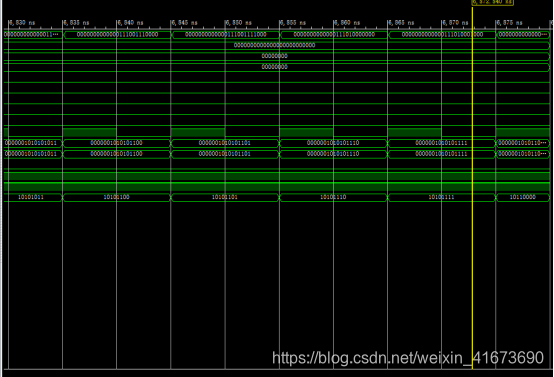
当start信号=0时,将仿真出的Xk数据导出就可以了
本人对于FFT的浅显理解,希望能对你有帮助!