k-NN 及 距离/相似度 计算
k-NN classification
- k的值要选择奇数,避免比如 k=4时, result : 2:2;或者 k=4时, result : 3:3 这种无法决策的情况出现
-
那么k到底选择什么值合适呢?
– 根据数据集大小选择
– 增加k的值,在验证数据集上测试准确性,选择最合适的k值 -
说到验证数据集,这里就介绍一下
– 验证数据集是从训练数据集中分出来的一部分,一般是训练数据集的20%
– 验证数据集一般用来选择超参数(超参数不是在训练过程中学习到的,它是在训练前就设置好的,不如说KNN中的k值就是超参数,所以在验证数据集中调试超参数)

Euclidean Distance(欧几里德距离)

import numpy as np
def distEuclid(x, y):
distance= np.sqrt(np.sum(np.square(x-y)))
return distance
x = np.array([1, 2])
y = np.array([3, 4])
distance = distEuclid(x, y)
print(distance)
#2.8284271247461903
Manhattan Distance(曼哈顿距离)
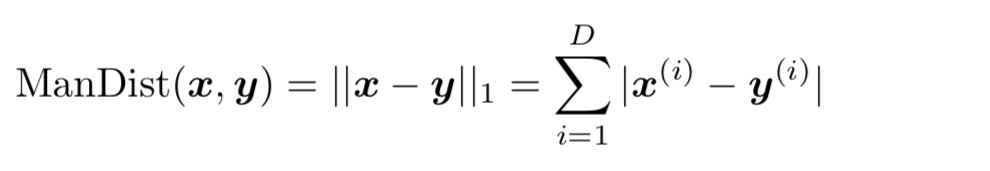
import numpy as np
def distManhatten(x, y):
distance = sum(abs(x-y))
return distance
x = np.array([1, 2])
y = np.array([3, 4])
distance = distManhatten(x, y)
print(distance)
#4
Cosine Similarity(余弦相似度)
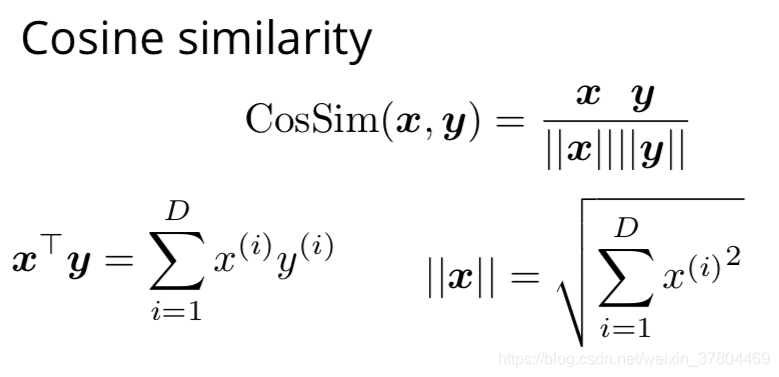
import numpy as np
def cosine_similarity(x, y):
a = y.dot(x.T)
b = np.sqrt(np.sum(x**2) * np.sum(y**2))
similarity = a / b
return similarity
x = np.array([1, 2])
y = np.array([3, 4])
distance = cosine_similarity(x, y)
print(distance)
Vector norms(向量范数)
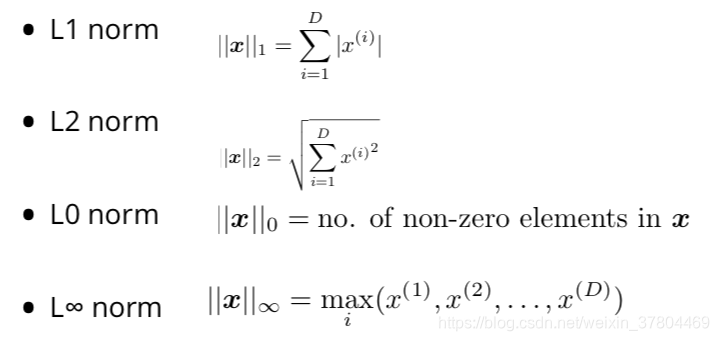
版权声明:本文为weixin_37804469原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。