1.定义
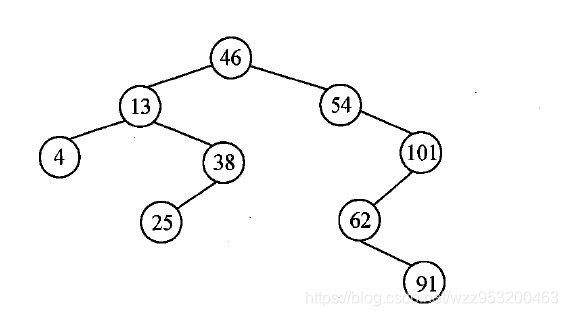
二叉排序树
又称为
二叉查找树
,它或者是一颗空树,或者有以下性质的树:
- 若它的左子树非空,则左子树上所有结点的值均小于根结点的值
- 若它的右子树非空,则右子树上所有结点的值均大于根结点的值
- 左、右子树本身是二叉排序树
2.查找过程
因为二叉排序树的
左子树上所有结点的关键字均小于根结点的关键字,右子树上所有结点的关键字均大于根结点的关键字
,所以在二叉排序树上进行查找的过程为:
- 二叉排序树非空时,将给定值与根结点的关键字值相比较,若相等,则查找成功;
- 若不相等,则当根结点的关键字值大于给定值时,下一步到根的左子树中进行查找,否则到根的右子树中进行查找;
- 若查找成功,则查找过程是走了一条从树根到所找到结点的路径;
- 否则,查找过程终止于一颗空的子树。
二叉排序树的查找算法:
typedef struct Tnode
{
int data; //结点的关键字值
struct Tnode *lchild,*rchild; //指向左、右子树的指针
}BSTnode,*BSTree;
//查找算法,root指向根,查找值为key的结点
BSTree SearchBST(BSTree root,int key,BSTree *father)
{
BSTree p = root;
*father = NULL;
while(p && p->data != key)
{
*father = p;
if(key < p->data)
p = p->lchild;
else
p = p->rchild;
}
return p;
}
3.插入过程
依次输入数据元素并把它们插入到二叉树的适当位置构造起来,每读入一个元素,建立一个新结点。
- 若二叉排序树非空,则将新结点的值与根结点的值相比较;
- 如果小于根结点的值,则插入到左子树,否则插入到右子树中;
- 若二叉排序树为空,则新结点作为二叉排序树的根结点;
插入{46,25,54,13,29,91}关键字序列示意图:
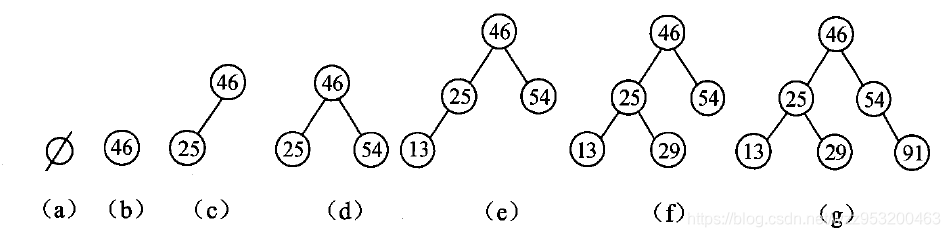
二叉排序树的插入算法:
//二叉排序树的插入算法
int InsertBST(BSTree *root,int newkey)
{
BSTree s,p,f;
s = (BSTree)malloc(sizeof(BSTnode));
if(!s)
return -1;
s->data = newkey;
s->lchild = NULL;
s->rchild = NULL;
p = SearchBST(*root,newkey,&f); //调用查找算法,查询插入位置
if(p)
return -1;
if(!f)
*root = s;
else if(newkey < f->data)
f->lchild = s;
else
f->rchild = s;
return 0;
}
4.删除过程
假设在二叉排序树中删除结点*p(p指向被删除结点),*f为其双亲结点,分为3种情况:
- 结点*p为叶子结点;
- 结点*p只有在左子树或者只有右子树;
- 结点*p的左子树均存在;
1)若*p为叶子结点且不是根结点,即p->lchild = NULL且p->rchild = NULL,由于删去叶子结点后不破坏整棵树的结构,因此只需修改*p的双亲结点*f的相应指针即可。
f->lchild(或f->rchild) = NULL;
2)若结点*p只有左子树或者只有右子树且*p不是根结点,此时只要将*p的左子树或右子树接成其双亲结点*f的左子树(或右子树)即可。
f->lchild(或f->rchild) = p->lchild; 或 f->lchild(或f->rchild) = p->rchild;
3)若*p结点的左、右子树均不空,则删除*p结点时应将其左子树、右子树连接到适当的位置,并保持二叉排序树的特性。可采用以下两种方法进行处理:
①令*p的左子树为*f的左子树(若*p不是根结点且*p是*f的左子树,否则为右子树),而将右子树下接到中序遍历时*p的直接前驱结点*s(*s结点是*p的左子树中最右下方的结点)的右孩子指针上;
②用*p的中序直接前驱(或后继)结点*s代替*p结点,然后删除*s结点

从二叉排序树的定义可知,中序遍历二叉排序树可得到一个关键字有序的序列;所以一个无序序列可以通过构造一棵二叉排序树而得到一个有序序列,构造二叉排序树的过程就是对无序序列进行排列的过程。