首先
,在试图弄懂AUC和ROC曲线之前,一定,一定要彻底理解
混淆矩阵
的定义!!!
混淆矩阵中有着Positive、Negative、True、False的概念,其意义如下:
-
称预测类别为1的为Positive(阳性),预测类别为0的为Negative(阴性)。
-
预测正确的为True(真),预测错误的为False(伪)。
对上述概念进行组合,就产生了如下的混淆矩阵:
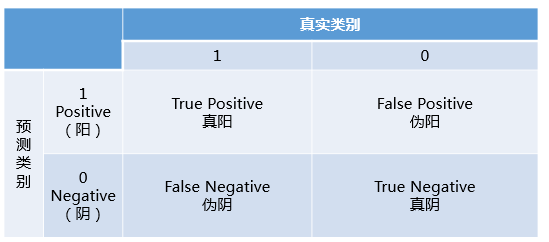
然后
,由此引出True Positive Rate(真阳率)、False Positive(伪阳率)两个概念:
-
-
- Precision = TP/TP+FP,预测为真的当中,实际为真的比例(越大越好,1为理想状态)
- Recall = TPRate,所有真实类别为1的样本中,预测类别为1的比例,即召回率(召回了多少正样本比例);
仔细看这两个公式,发现其实TPRate就是TP除以TP所在的列,FPRate就是FP除以FP所在的列,二者意义如下:
-
TPRate的意义是所有真实类别为1的样本中,预测类别为1的比例。
-
FPRate的意义是所有真是类别为0的样本中,预测类别为1的比例。
- precision的含义是:
如果上述概念都弄懂了,那么ROC曲线和AUC就so easy了:
按照定义,AUC即ROC曲线下的面积,而ROC曲线的横轴是FPRate,纵轴是TPRate,当二者相等时,即y=x,如下图,表示的意义是:
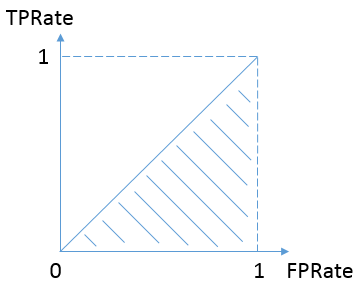
对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的。换句话说,和抛硬币并没有什么区别,一个抛硬币的分类器是我们能想象的最差的情况,因此一般来说我们认为AUC的最小值为0.5(当然也存在预测相反这种极端的情况,AUC小于0.5)。而我们希望分类器达到的效果是:对于真实类别为1的样本,分类器预测为1的概率(即TPRate),要大于真实类别为0而预测类别为1的概率(即FPRate),这样的ROC曲线是在y=x之上的,因此大部分的ROC曲线长成下面这个样子:
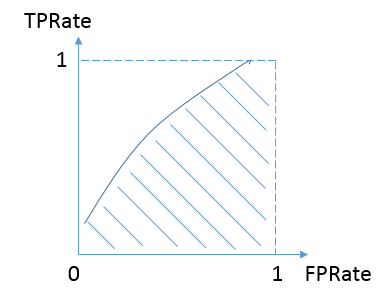
最理想的情况下,没有真实类别为1而错分为0的样本,TPRate一直为1,于是AUC为1,这便是AUC的极大值。
说了这么多还是不够直观,不妨举个简单的例子。
首先对于硬分类器(例如SVM,NB),预测类别为离散标签,对于8个样本的预测情况如下:

得到混淆矩阵如下:
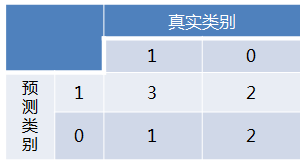
进而算得TPRate=3/4,FPRate=2/4,得到ROC曲线:
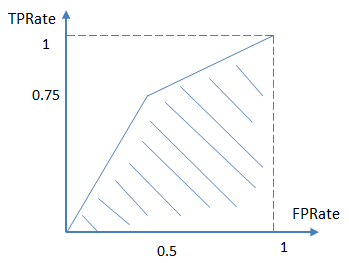
最终得到AUC为0.625。
对于LR等预测类别为概率的分类器,依然用上述例子,假设预测结果如下:

这时,需要设置阈值来得到混淆矩阵,不同的阈值会影响得到的TPRate,FPRate,如果阈值取0.5,小于0.5的为0,否则为1,那么我们就得到了与之前一样的混淆矩阵。其他的阈值就不再啰嗦了。依次使用所有预测值作为阈值,得到一系列TPRate,FPRate,描点,求面积,即可得到AUC。
最后说说AUC的优势,AUC的计算方法同时考虑了分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价。
例如在反欺诈场景,设非欺诈类样本为正例,负例占比很少(假设0.1%),如果使用准确率评估,把所有的样本预测为正例便可以获得
99.9%的准确率
。
但是如果使用AUC,把所有样本预测为正例,TPRate和FPRate同时为1,
AUC仅为0.5
,成功规避了样本不均匀带来的问题。
ROC曲线的Python实现实例
#!/usr/bin/env python
# -*- coding:UTF-8 -*-
import numpy as np
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
y = np.array([0,0,1,1])
pred = np.array([0.1,0.4,0.35,0.8])
fpr, tpr, thresholds = roc_curve(y, pred, pos_label=1)
print "fpr:",fpr
print "tpr:",tpr
print "thresholds:",thresholds
#画对角线
plt.plot([0, 1], [0, 1], '--', color=(0.6, 0.6, 0.6), label='Luck')
#画ROC曲线
plt.plot(fpr,tpr,lw=1,label = "ROC curve")
plt.show()
from sklearn.metrics import auc
print "auc:",auc(fpr, tpr)
#result
fpr: [ 0. 0.5 0.5 1. ]
tpr: [ 0.5 0.5 1. 1. ]
thresholds: [ 0.8 0.4 0.35 0.1 ]
auc: 0.75
计算过程解析:
测试样本有真实标签和预测概率:
| 真实标签label | 0 | 0 | 1 | 1 |
| 预测概率p | 0.1 | 0.4 | 0.35 | 0.8 |
按预测概率从小到大或从大到小排序,依次选取概率值为阈值。
| 真实标签label | 1 | 0 | 1 | 0 |
| 预测概率p | 0.8 | 0.4 | 0.35 | 0.1 |
sklearn是按照概率值从大到小排序来计算FTPR和TPR的,本文下面也按照这种排序方式,以便于理解。
当选择0.8为分隔阈值时,当p>=0.8时,认为该样本为正样本,否则为负样本,结果如下:
| 真实标签label | 1 | 0 | 1 | 0 |
| 预测标签: | 1 | 0 | 0 | 0 |
| 预测概率p | 0.8 | 0.4 | 0.35 | 0.1 |
根据混淆矩阵得到

则TP = 1,FN = 1, FP = 0,TN = 2;则计算得到FPR =FP/FP+TN= 0/0+2=0,TPR = TP/TP+FN=1/1+1=0.5.
当选择0.4为分隔阈值时,当p>=0.4时,认为该样本为正样本,否则为负样本,结果如下:
| 真实标签label | 1 | 0 | 1 | 0 |
| 预测标签: | 1 | 1 | 0 | 0 |
| 预测概率p | 0.8 | 0.4 | 0.35 | 0.1 |
则TP = 1,FN = 1, FP = 1,TN = 1;则计算得到FPR =FP/FP+TN= 1/1+1=0.5,TPR = TP/TP+FN=1/1+1=0.5.
当选择0.35为分隔阈值时,当p>=0.35时,认为该样本为正样本,否则为负样本,结果如下:
| 真实标签label | 1 | 0 | 1 | 0 |
| 预测标签: | 1 | 1 | 1 | 0 |
| 预测概率p | 0.8 | 0.4 | 0.35 | 0.1 |
则TP = 2,FN = 0, FP = 1,TN = 1;则计算得到FPR =FP/FP+TN= 1/1+1=0.5,TPR = TP/TP+FN=2/2+0=1.
当选择0.1为分隔阈值时,当p>=0.1时,认为该样本为正样本,否则为负样本,结果如下:
| 真实标签label | 1 | 0 | 1 | 0 |
| 预测标签: | 1 | 1 | 1 | 1 |
| 预测概率p | 0.8 | 0.4 | 0.35 | 0.1 |
则TP = 2,FN = 0, FP = 2,TN = 0;则计算得到FPR =FP/FP+TN= 2/2+0=1,TPR = TP/TP+FN=2/2+0=1.
参考:https://www.zhihu.com/question/39840928/answer/241440370