描述

给定节点数为 n 二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。

例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。



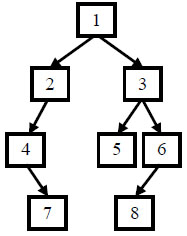
输入：[1,2,4,7,3,5,6,8],[4,7,2,1,5,3,8,6]

返回值：{1,2,3,4,#,5,6,#,7,#,#,8}

说明：

返回根节点，系统会输出整颗二叉树对比结果，重建结果如题面图示

提示:

1.vin.length == pre.length

2.pre 和 vin 均无重复元素

3.vin出现的元素均出现在 pre里

4.只需要返回根结点，系统会自动输出整颗树做答案对比

要求：空间复杂度 O(n)，时间复杂度 O(n)

解题思路:递归

二叉树定义（c++)

struct TreeNode{
	int val;
	TreeNode* left;
	TreeNode* right;
	TreeNode(int x): val(x), left(NULL), right(NULL){}
};

class Solution {
public:
    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {//pre前序遍历数组，vin中序遍历数组
        if(pre.empty()||vin.empty()) return NULL;
        int rootVal = pre[0];//前序遍历第一个值为根结点
        int rootInIndex = find(vin.begin(),vin.end(),rootVal)-vin.begin();//在中序遍历里找到根结点的位置
        TreeNode* root = new TreeNode(rootVal);
        //切割中序
        vector<int> newInorderLeft(vin.begin(),vin.begin()+rootInIndex);//切割中序左子树
        vector<int> newInorderRight(vin.begin()+rootInIndex+1,vin.end());//切割中序右子树
        //切割前序
        vector<int> newPreorderLeft(pre.begin()+1,pre.begin()+1+newInorderLeft.size());//切割前序左子树
        vector<int> newPreorderRight(pre.begin()+1+newInorderLeft.size(),pre.end());//切割前序右子树
        //递归调用
        root->left = reConstructBinaryTree(newPreorderLeft, newInorderLeft);
        root->right = reConstructBinaryTree(newPreorderRight, newInorderRight);
        return root;
       
    }
};