找零时，兑换最少个数的硬币

一、贪心策略

贪心，就是每次都试图解决问题的

尽量大

的一部分

从最大面值的硬币开始，用尽量多的数量，有余额的再到下一个面值

# 贪心
def change(coinValueList, money):
    '''
    贪心策略
    :param coinValueList: 硬币体系
    :param money: 找零的币值
    :return: 找零所需硬币数
    '''
    coinValueList = sorted(coinValueList, reverse=True)
    num = [0] * len(coinValueList)
    for k in range(len(coinValueList)):
        num[k] = money // coinValueList[k]
        money = money % coinValueList[k]
    if money == 0:
        return sum(num)

print(change([1, 5, 10, 25], 63))
print(change([25, 21, 10, 5, 1], 63))
print(change([50,25,10,5,1], 49))

def change(coinValueList, money):
    '''
    贪心策略简化
    :param coinValueList: 硬币体系
    :param money: 找零的币值
    :return: num 找零所需硬币数
    '''
    coinValueList = sorted(coinValueList, reverse=True)
    num = 0
    for c in coinValueList:
        if c <= money:
            num += money // c
            money = money % c
    if money == 0:
        return num

print(change([1, 5, 10, 25], 63))
print(change([25, 21, 10, 5, 1], 63))
print(change([50,25,10,5,1], 49))

其实币值是按贪心策略设计的，对于某些情况贪心策略会失效。如果币值特殊，比如有21元，币值体系有25，21，10，5，1，那么对于找零63元，最少硬币数是3，但是如果按贪心策略，最少硬币数是2+1+3 = 6

二、递归解法

递归体现了分治策略split and merge，递归三定律：基本结束条件、缩小规模、调用自身。

def change(coinValueList, money):
	if money in coinValueList:  # 结束条件
		return 1
		
	min = money
	for i in [c for c in coinValueList if c <= change]:  # 缩小规模
		num = 1 + change(coinValueList, money - i)  # 每次减去一种币值
		if num < min:  # 每次挑选最小数量
			num = min  # for循环里面这个结构常用于找到每次最小或最大
		return min 

print(change([1, 5, 10, 25], 63))
print(change([25, 21, 10, 5, 1], 63))

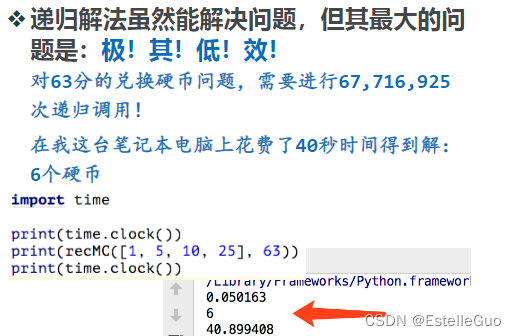
import time
# 不知为啥，我用上面的clock不行
t1 = time.process_time()
print(change([1, 5, 10, 25], 63))
t2 = time.process_time()
print('time:', t2-t1)

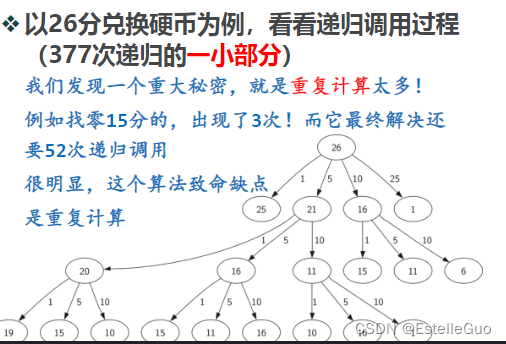
def change(coinValueList, money, knownResults):
	min = money
	if money in coinValueList:
		knownResults[money] = 1
		return 1
	elif knownResults[money] > 0:  # 查表成功
		return knownResults[money]
	else:
		for i in [c for c in coinValueList if c <= money]:
			num = 1 + change(coinValueList, money - i, knownResults)
			if num < min:
				min = num
				knownResults[money] = min
	return min


print(change([25, 21, 10, 5, 1], 63, [0] * 64))			

缓存：还有很多其它应用

三、动态规划解法

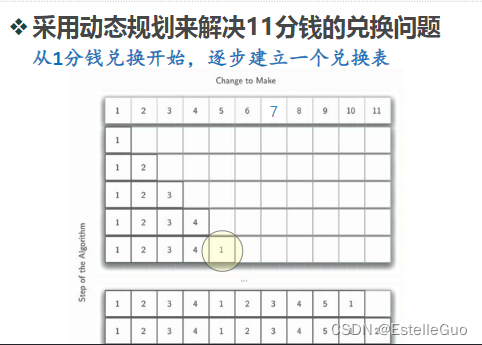
def dpchange(coinValueList, money, min):
    # 从1分开始到money逐个计算最少硬币数
    for cents in range(1, money + 1):
        # 1. 初始化一个最大值
        coinCount = money
        # 2. 减去每个硬币，向后查最少硬币数，同时记录总的最少数
        for j in [c for c in coinValueList if c <= cents]:
            if min[cents - j] < coinCount:
                coinCount = min[cents - j] + 1
        # 3. 得到当前最少硬币数，记录到表中
        min[cents] = coinCount
    # 返回最后一个结果
    return min[money]

print(dpchange([1, 5, 10, 21, 25], 63, [0] * 64))
print(dpchange([1, 5, 10, 25], 63, [0] * 64))

def dpchange(coinValueList, money, min, coinsUsed):
    # 从1分开始到money逐个计算最少硬币数
    for cents in range(money + 1):
        # 1. 初始化一个最大值
        coinCount = money
        newCoin = 1   # 初始化一下新加硬币
        # 2. 减去每个硬币，向后查最少硬币数，同时记录总的最少数
        for j in [c for c in coinValueList if c <= cents]:
            if min[cents - j] < coinCount:
                coinCount = min[cents - j] + 1
                newCoin = j  # 对应最小数量，所减的硬币
        # 3. 得到当前最少硬币数，记录到表中
        min[cents] = coinCount
        coinsUsed[cents] = newCoin  # 记录本步骤加的一枚硬币
    # 返回最后一个结果
    return min[money]

def printCoins(coinsUsed, money):
    coin = money
    while coin > 0:
        thisCoin = coinsUsed[coin]
        print(thisCoin)
        coin = coin - thisCoin


money = 63
clist = [1, 5, 10, 21, 25]
coinsUsed = [0] * (money + 1)
coinCount = [0] * (money + 1)

print('Making change for', money, "requires")
print(dpchange(clist, money, coinCount, coinsUsed), 'coins')
print('They are:')
printCoins(coinsUsed, money)
print('The used list is as follows:')
print(coinsUsed)

Making change for 63 requires

3 coins

They are:

21

21

21

The used list is as follows:

[0, 1, 1, 1, 1, 5, 5, 5, 5, 5, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 21, 21, 21, 21, 25, 25, 25, 25, 25, 25, 21, 21, 21, 21, 25, 25, 25, 25, 25, 25, 21, 21, 21, 21, 25, 25, 25, 25, 25, 25, 25, 21, 21, 21, 25, 25, 25, 25, 25, 25, 25, 21, 21]

好像有点问题哎，求大佬指点