atan2
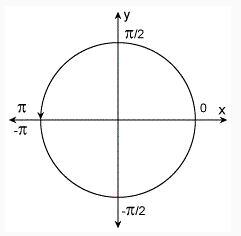
求的是一个点所对应的角的大小 ,且输出角度范围是【-π, π】
atan
求的是一个数值对应的角,且输出角度范围是【-π/2, π/2】
例如:
atan(1)=0.7854
atan(1,1)=0.7854
c1 = atan2(sqrt(3), 3)*180/pi; % result = 30 点(3, sqrt(3))
c2 = atan2(sqrt(3), 1)*180/pi; % result = 60 点(1, sqrt(3))
c3 = atan2(-sqrt(3), 1)*180/pi; % result = -60 点(1, -sqrt(3))
c4 = atan2(-sqrt(3), 3)*180/pi; % result = -30 点(3, -sqrt(3))
c31 = atan2(sqrt(3), -1)*180/pi; % result = 120 点(-1, sqrt(3))
c41 = atan2(sqrt(3), -3)*180/pi; % result = 150 点(-3, sqrt(3))
c5 = atan2(-sqrt(3), -3)*180/pi; % result = -150 点(-3, -sqrt(3))
c6 = atan2(-sqrt(3), -1)*180/pi; % result = -120 点(-1, -sqrt(3))
c7 = atan2(-sqrt(3), 3)*180/pi; % result = -30 点(3, -sqrt(3))
c8 = atan2(-sqrt(3), 1)*180/pi; % result = -60 点(1, -sqrt(3))

注意以下说明中均
针对点(b, a),注意atan2使用时参数的先后顺序为a,b
atan2(a,b)
是4象限反正切,它的取值不仅取决于正切值a/b,还取决于点 (b, a) 落入哪个象限
当点(b, a) 落入第一象限时,atan2(a,b)的范围是 0 ~ pi/2;
当点(b, a) 落入第二象限时,atan2(a,b)的范围是 pi/2 ~ pi;
当点(b, a) 落入第三象限时,atan2(a,b)的范围是 -pi/2~0;
当点(b, a) 落入第四象限时,atan2(a,b)的范围是 -pi~-pi/2
而 atan(a/b) 仅仅根据正切值为a/b求出对应的角度
(可以看作仅仅是2象限反正切)
当 a/b > 0 时,atan(a/b)取值范围是 0 ~ pi/2;
当 a/b < 0 时,atan(a/b)取值范围是 -pi/2~0
故 atan2(a,b) = atan(a/b) 仅仅发生在 点 (b, a) 落入第一象限 (b>0, a>0)或 第三象限(b>0, a<0)。
当点 (b, a) 落入第二、三象限时,很显然atan2(a,b) 不等于 atan(a/b) ,并且atan2(a,b)也不可能等于 2*atan(a/b) 。


(a)常用坐标系 (b)图像坐标系(顺时针旋转90°)
针对不同坐标系角度变化问题:
(1)可以只记住常用坐标系下(MATLAB默认的计算atan、atan2的坐标系)的atan、atan2角度取值方式,见图(a)。其他坐标系的角度取值方式就是在图(a)坐标系下的旋转、对称等变换。如图(b)就是由默认坐标系图(a)经顺时针旋转90°(π/2)得到,即原坐标系+(π/2)得到,对于+(π/2)超出[-π, π]的情况,只需再在此基础上±2π即可,(图(a)除了左上角那个象限需+π/2-2π外,其他象限只需+π/2,但三角函数计算时(α+π/2-2π) = (α+π/2),因此进行方向合成时无需±2π)。
(2)在图(b)坐标系下计算atan、atan2时,只需利用图(b)坐标系下的dx、dy或点坐标,直接使用atan、atan2函数计算,计算得到的结果是图(b)坐标系下的弧度值。由此结果再逆时针旋转90°(减去π/2),即得到图(a)坐标系下的弧度值。
(3)同理,也可在图(a)坐标系下的dx、dy或点坐标,使用atan、atan2函数计算,此结果再顺时针旋转90°(π/2)即可得到图(b)坐标系下的弧度值。
(4)另外,针对求沿某特定方向的倾斜、曲率问题,只需将沿某坐标系下的x、y轴正方向的倾斜、曲率与该坐标系下所求特定方向的角度,利用方向合成公式计算即可。