一. 冒泡排序
1. 思想:利用比较相邻的两个元素,发现两个数前者大于后者则进行交换,这样每一轮可以把最大数放到后面,只要做n轮便可以使得序列有序。
2. 举例,例如序列 8 7 3 4 5 0 1
第一轮:8 7 3 4 5 0 1
8 7
3 4 5 0 1 -> 7 8 3 4 5 0 1
7
8 3
4 5 0 1 -> 7 3 8 4 5 0 1
7 3
8 4
5 0 1 -> 7 3 4 8 5 0 1
7 3 4
8 5
0 1 -> 7 3 4 5 8 0 1
7 3 4 5
8 0
1 -> 7 3 4 5 0 8 1
7 3 4 5 0
8 1
-> 7 3 4 5 0 1
8 // 得到最大值8在最后一个位置
第二轮:7 3 4 5 0 1
………..
3. 从上面的例子我们可以知道,冒泡排序的时间复杂度为O(n^2),不需要额外的空间辅助,是一个稳定的算法
4. 示例代码
#include<iostream>
#include<algorithm>
using namespace std;
//冒泡排序
void BubbleSort(int *arrNum, int n){
//数据不合法
if(arrNum == NULL || n <= 0){
return;
}
for(int i = 0; i < n; i++){
for(int j = 0; j < (n-i-1); j++){
if(arrNum[j] > arrNum[j+1]){
swap(arrNum[j], arrNum[j+1]);
}
}
}
}
int main(){
//test
int arrNum[] = {8,7,3,4,5,0,1};
BubbleSort(arrNum, 7);
for(int i = 0; i < 7; i++){
cout<<arrNum[i]<<" ";
}
cout<<endl;
//输出 0 1 3 4 5 7 8
getchar();
return 0;
}
二. 插入排序
1. 思想:每次选择未排序序列的第一个数插入已经排好序的序列中,使得这个序列依然有序
2. 举例:
例如序列 8 7 3 4 5 0 1
第一次:未排序序列为8 7 3 4 5 0 1,第一个数是8,没有排好的序列,因此排好序列为8
第二次:未排序序列为7 3 4 5 0 1,第一个数7,排好序序列为8,则插入到8前面,序列为7 8
第三次:未排序序列为3 4 5 0 1,第一个数为3,排好序序列为3,则插入到7前面,序列为3 7 8
……..
3. 只要把所有的未排序的数全部插入到已经排好序的序列中,这样整个序列就是有序的。时间复杂度为O(n^2),是一个稳定的排序算法
4. 示例代码
#include<iostream>
#include<algorithm>
using namespace std;
//插入排序
void InsertSort(int *arrNum, int n){
//数据不合法
if(arrNum == NULL || n <= 0){
return;
}
for(int i = 1; i < n; i++){
int tmp = arrNum[i];
int j;
for(j = i-1; j >= 0; j--){
//如果比tmp大把值往后移动一位
if(arrNum[j] > tmp){
arrNum[j+1] = arrNum[j];
}
else{
break;
}
}
arrNum[j+1] = tmp;
}
}
int main(){
//test
int arrNum[] = {8,7,3,4,5,0,1};
InsertSort(arrNum, 7);
for(int i = 0; i < 7; i++){
cout<<arrNum[i]<<" ";
}
cout<<endl;
//输出 0 1 3 4 5 7 8
getchar();
return 0;
}
三. 选择排序
1. 思想:每次从未排序的序列中选择一个最小的数未排序序列第一个数交换,相当于每次选择一个最小的数放到排好序的序列最后一个位子,当未排序序列为空的时候整个序列即为有序
2. 举例:例如序列8 7 3 4 5 0 1
第一次:序列 8 7 3 4 5 0 1,未排序序列最小的数0,和8交换,此时排好序序列为0
第二次:序列
0
7 3 4 5 8 1,未排序序列最小的数1,和7交换,此时排好序序列为0 1
第三次:序列
0 1
3 4 5 8 7,未排序序列最小的数3,本身不用交换,此时排好序序列为0 1 3
……………
3. 当未排序序列为空的时候说明整个序列为有序,时间复杂度为O(n^2),是一个不稳定的排序算法
4. 示例代码
#include<iostream>
#include<algorithm>
using namespace std;
//插入排序
void SelectSort(int *arrNum, int n){
//数据不合法
if(arrNum == NULL || n <= 0){
return;
}
for(int i = 0; i < n; i++){
int minNumIndex = i;
for(int j = i+1; j < n; j++){
if(arrNum[j] < arrNum[minNumIndex]){
minNumIndex = j;
}
}
//找到最小值直接和未排序第一个数交换
if(i != minNumIndex){
swap(arrNum[i], arrNum[minNumIndex]);
}
}
}
int main(){
//test
int arrNum[] = {8,7,3,4,5,0,1};
SelectSort(arrNum, 7);
for(int i = 0; i < 7; i++){
cout<<arrNum[i]<<" ";
}
cout<<endl;
//输出 0 1 3 4 5 7 8
getchar();
return 0;
}
四. 快速排序
1. 思想:利用一个基准arrNum[k]每次把区间[l,r]划分成两个部分[l,k-1],[k+1,r]使得[l,k-1]这个子区间的所有值全部小于等于arrNum[k],[k+1,r]这个区间的值全部大于等于arrNum[k]的值,然后递归对这两个子区间进行排序。
2. 举例:例如序列8 7 3 4 5 0 1,每次选择区间中间那个数作为基准
第一次:区间为[0, 6],选择基准为arrNum[3] = 4
(1)先把基准4和最后一个数交换,得到8 7 3 1 5 0
4
(2)设置两个指针p1和p2,p1用来枚举所有数,p2用来保存左子区间全部小于基准的下标,初始化p1和p2都是指向区间左端点
(3)手动推算结果如下
3. 快速排序时间复杂度为O(NlogN),是一个不稳定的算法,有可能会退化为O(n^2),不需要额外的空间
4. 示例代码
#include<iostream>
#include<algorithm>
using namespace std;
//划分区间
int Partition(int *arrNum , int l, int r){
//左子区间结束下标
int leftSeqIndex = l;
int mid = (l+r)>>1;
//把基准值交换到最后一个位置
swap(arrNum[mid], arrNum[r]);
//O(n)时间划分
for(int i = l; i < r; i++){
if(arrNum[i] < arrNum[r]){
if(leftSeqIndex < i){
swap(arrNum[leftSeqIndex], arrNum[i]);
}
++leftSeqIndex;
}
}
//把基准交换回原来的位置
swap(arrNum[leftSeqIndex], arrNum[r]);
return leftSeqIndex;
}
//快速排序
void QuickSort(int *arrNum, int l, int r){
//数据不合法
if(arrNum == NULL || l >= r){
return;
}
int index = Partition(arrNum, l, r);
if(l < index){
QuickSort(arrNum, l, index-1);
}
if(index < r){
QuickSort(arrNum, index+1, r);
}
}
int main(){
//test
int arrNum[] = {8,7,3,4,5,0,1};
QuickSort(arrNum, 0, 6);
for(int i = 0; i < 7; i++){
cout<<arrNum[i]<<" ";
}
cout<<endl;
//输出 0 1 3 4 5 7 8
getchar();
return 0;
}
五. 归并排序
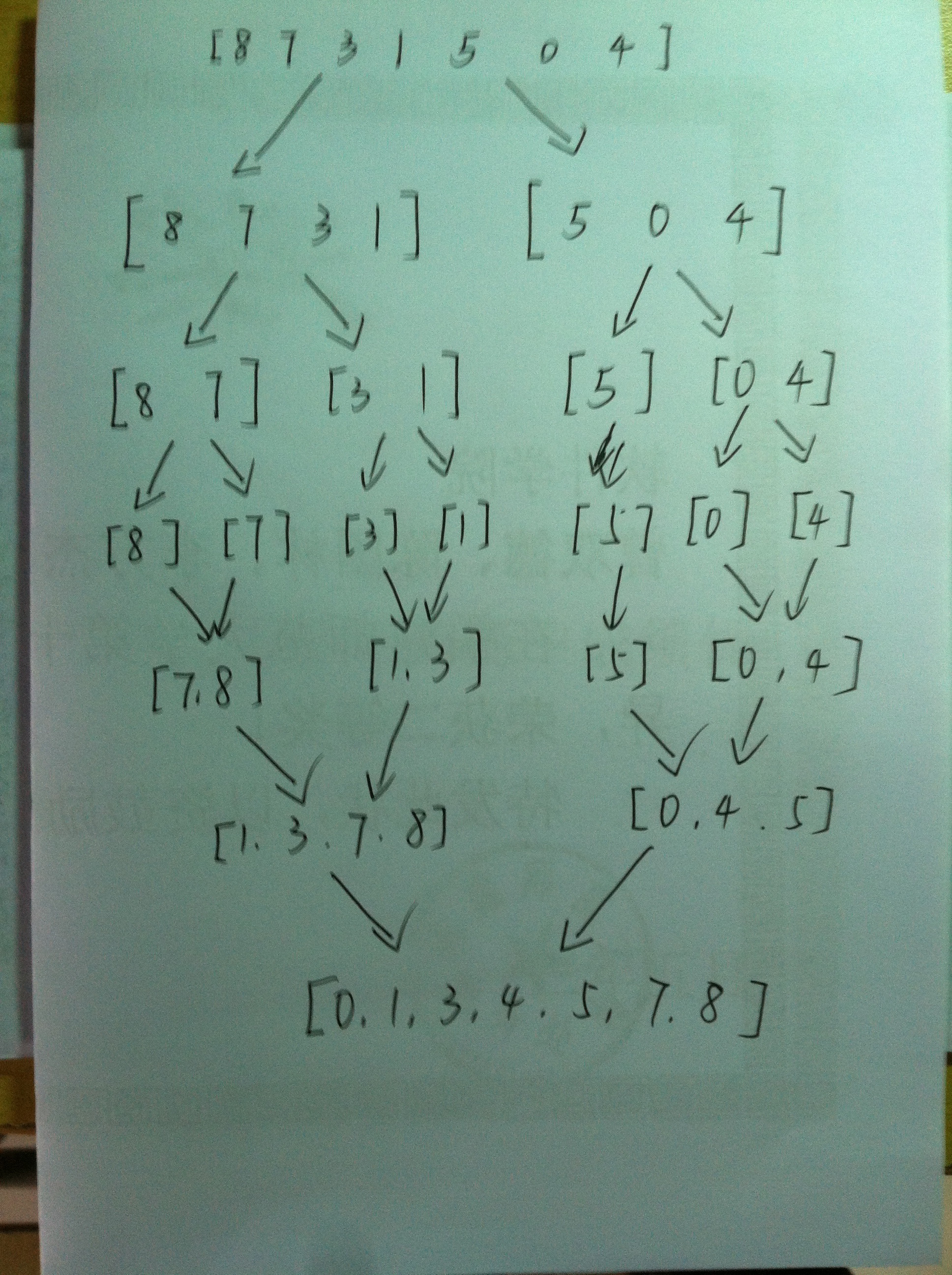
1. 思想:利用分治的思想,每次把要排序的区间平均划分成两部分,然后递归排序,再合并这两个区间
2. 举例:例如序列8 7 3 1 5 0 4
3. 归并排序的时间复杂度为O(NlogN),是一个稳定的排序算法,但是需用一个和原来一样大的内存空间
4. 示例代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 10;
//合并
void Merge(int *arrNum , int l, int mid, int r){
int i = l;
int j = mid+1;
int pos = l;
int tmpArrNum[N];
while(i <= mid && j <= r){
if(arrNum[i] <= arrNum[j]){
tmpArrNum[pos++] = arrNum[i++];
}
else{
tmpArrNum[pos++] = arrNum[j++];
}
}
//把没有排完的数
while(i <= mid){
tmpArrNum[pos++] = arrNum[i++];
}
while(j <= r){
tmpArrNum[pos++] = arrNum[j++];
}
//把数据拷贝回到原来数组
for(int i = l; i <= r; i++){
arrNum[i] = tmpArrNum[i];
}
}
//归并排序
void MergeSort(int *arrNum, int l, int r){
//数据不合法
if(arrNum == NULL || l >= r){
return;
}
int mid = (l+r)>>1;
MergeSort(arrNum, l, mid);
MergeSort(arrNum, mid+1, r);
Merge(arrNum, l, mid, r);
}
int main(){
//test
int arrNum[] = {8,7,3,4,5,0,1};
MergeSort(arrNum, 0, 6);
for(int i = 0; i < 7; i++){
cout<<arrNum[i]<<" ";
}
cout<<endl;
//输出 0 1 3 4 5 7 8
getchar();
return 0;
}
六. 堆排序
1. 堆排序利用堆的性质,最小堆满足根结点的值比左右子树都小,最大堆满足根结点的值比左右子树都大
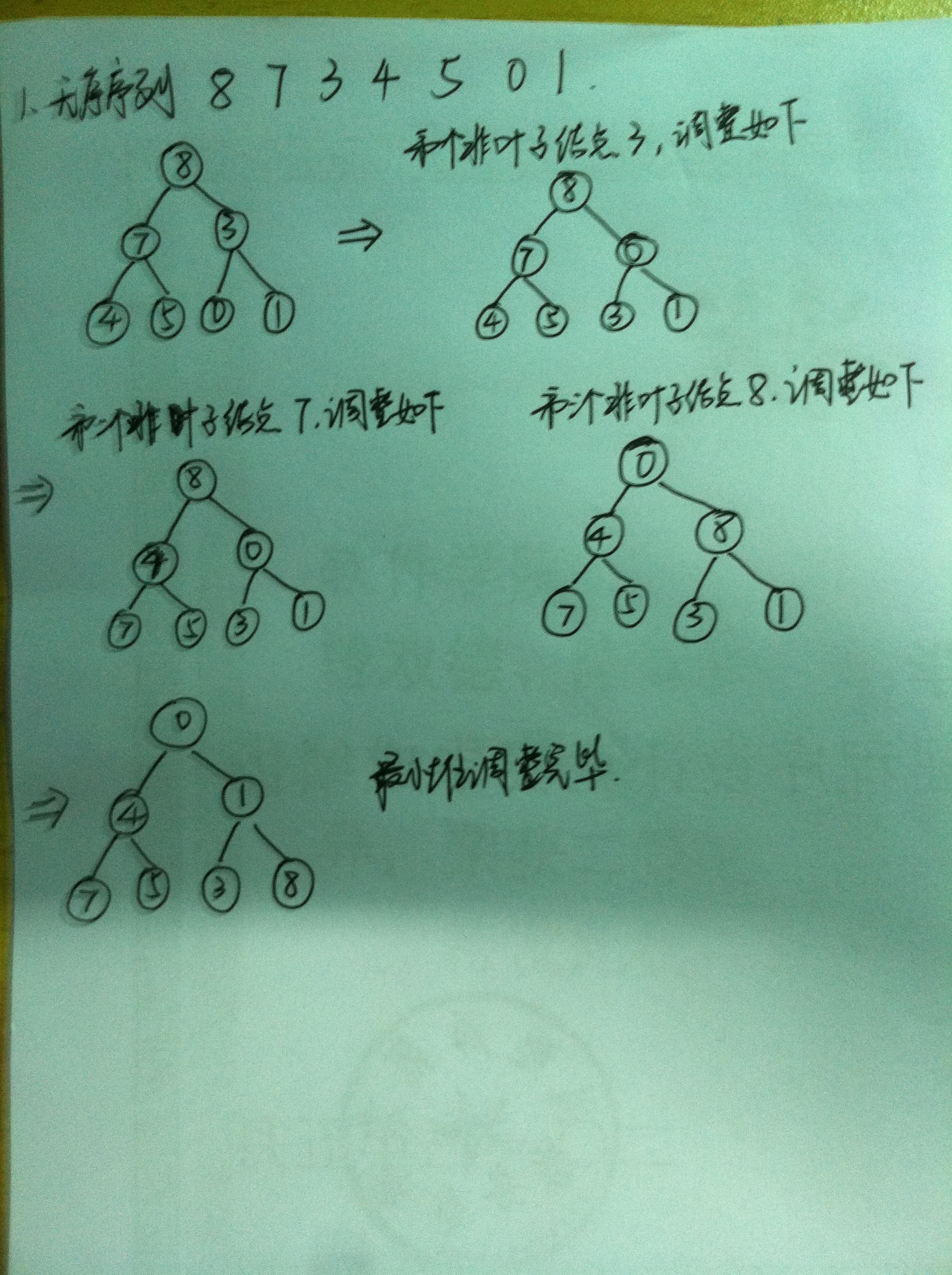
2. 一个无序系列建立最小堆方法是,从第一个叶子到根结点,每个结点往下调整,调整完所有结点之后即为最小堆
为什么叶子结点不用调整?因为叶子结点已经满足最小堆的性质
3. 一个无序序列调整为最小堆的过程,序列为8 7 3 4 5 0 1
4. 建立最小堆的时间复杂度为O(n),很多人认为是O(NlogN),为什么不是呢?证明如下
假设堆中有N个元素,则树高为H = logN,对于树高为h的结点建堆时间复杂度为O(H-h)。因此从最底层到根结点所有结点的建堆时间复杂度和为
S = 0*2^(H-1)+1*2^(H-2)+2*2^(H-3)+……..+(H-1)*2^0
<= 2^(H)+2^(H-1)+2^(H-2)+…….+2^0
<= 2^(H+1)
因为H = logN,则2^(H+1) = 2^H*2 = 2N,则时间复杂度为O(N)。
5. 建立最小堆代码
//向下调整
void AdjustDown(int *arrNum, int pos, int n){
int minIndex = pos;
int lsonIndex = pos<<1;
int rsonIndex = (pos<<1)+1;
if(lsonIndex <= n && arrNum[lsonIndex] < arrNum[minIndex]){
minIndex = lsonIndex;
}
if(rsonIndex <= n && arrNum[rsonIndex] < arrNum[minIndex]){
minIndex = rsonIndex;
}
if(minIndex != pos){
swap(arrNum[pos], arrNum[minIndex]);
AdjustDown(arrNum, minIndex, n);
}
}
//建立最小堆
void BuildHeap(int *arrNum, int n){
if(arrNum == NULL || n <= 0){
return;
}
//下标从1开始第一个非叶子结点编号为n/2
for(int i = n/2; i >= 1; i--){
//向下调整
AdjustDown(arrNum, i, n);
}
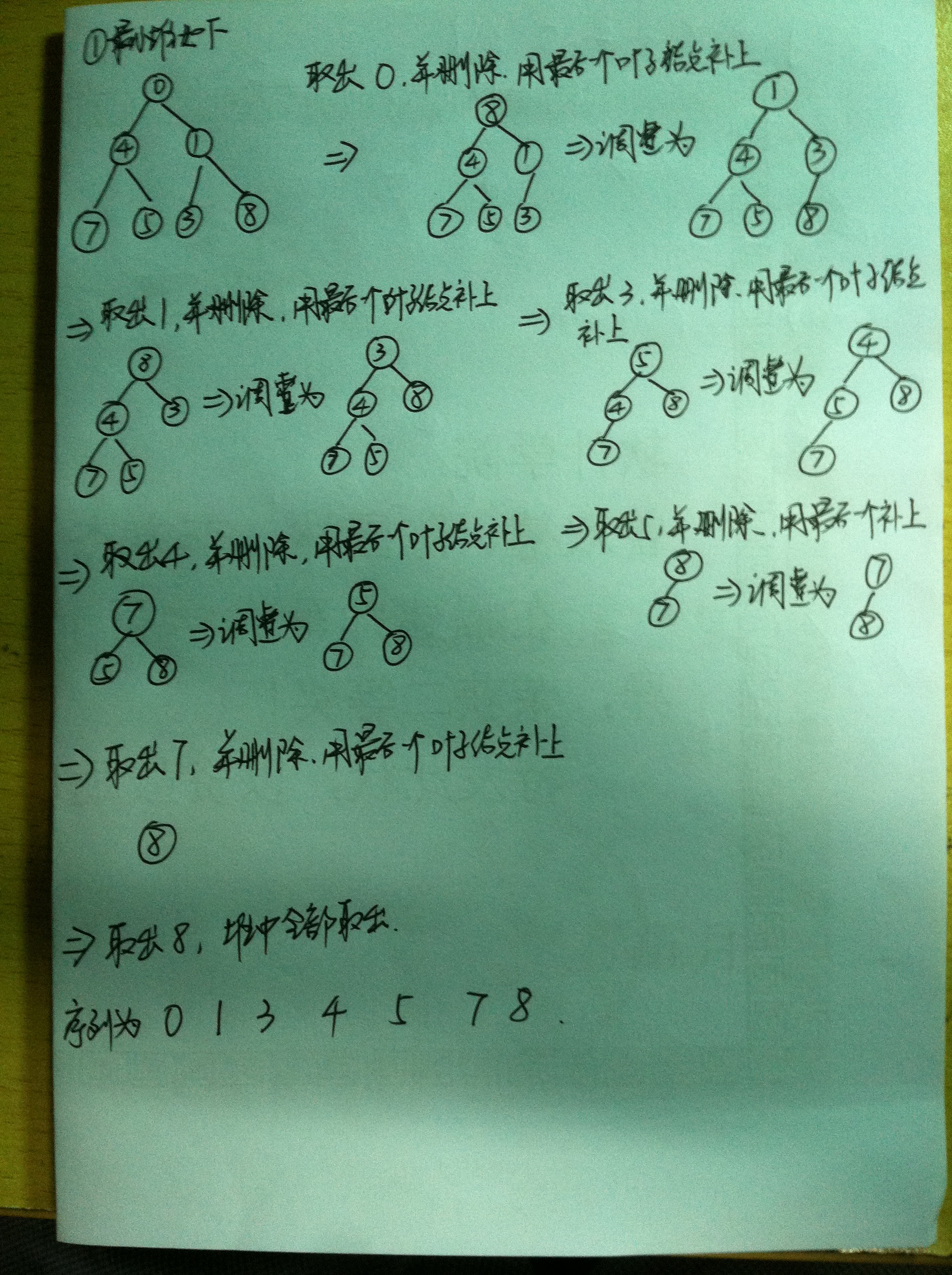
}6. 堆排序只需要每次把最小堆的根结点值取出并删除根结点,然后把最后一个叶子结点补到根结点并删除指,然后从根结点往下调整即可,时间复杂为O(NlogN),是一个不稳定的排序算法,不需要额外空间
#include<iostream>
#include<algorithm>
using namespace std;
//向下调整
void AdjustDown(int *arrNum, int pos, int n){
int minIndex = pos;
int lsonIndex = pos<<1;
int rsonIndex = (pos<<1)+1;
if(lsonIndex <= n && arrNum[lsonIndex] < arrNum[minIndex]){
minIndex = lsonIndex;
}
if(rsonIndex <= n && arrNum[rsonIndex] < arrNum[minIndex]){
minIndex = rsonIndex;
}
if(minIndex != pos){
swap(arrNum[pos], arrNum[minIndex]);
AdjustDown(arrNum, minIndex, n);
}
}
//建立最小堆
void BuildHeap(int *arrNum, int n){
if(arrNum == NULL || n <= 0){
return;
}
//下标从1开始第一个非叶子结点编号为n/2
for(int i = n/2; i >= 1; i--){
//向下调整
AdjustDown(arrNum, i, n);
}
}
void HeapSort(int *arrNum, int n){
//不合法数据
if(arrNum == NULL || n <= 0){
return;
}
int pos = 1;
while(pos <= n){
//每次输出根节点的值即为最小
cout<<arrNum[1]<<" ";
//把最后一个结点交换上去
swap(arrNum[1], arrNum[n-pos+1]);
//从根结点向下调整
AdjustDown(arrNum, 1, n-pos);
++pos;
}
}
int main(){
//test
int arrNum[] = {-1, 8,7,3,4,5,0,1};
BuildHeap(arrNum, 7);
HeapSort(arrNum, 7);
//输出 0 1 3 4 5 7 8
getchar();
return 0;
}
总结:
稳定排序算法:冒泡排序、插入排序、归并排序、基数排序
不稳定排序算法:选择排序、快速排序、堆排序、希尔排序